|
Пятискатная прямая куполоротонда
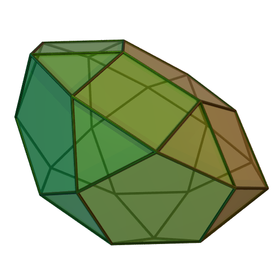
Пятиска́тная пряма́я куполорото́нда[1] — один из многогранников Джонсона (J32, по Залгаллеру — М6+М9). Составлена из 27 граней: 15 правильных треугольников, 5 квадратов и 7 правильных пятиугольников. Среди пятиугольных граней 1 окружена пятью квадратными, остальные 6 — пятью треугольными; каждая квадратная грань окружена пятиугольной и тремя треугольными; среди треугольных граней 5 окружены тремя пятиугольными, 5 — двумя пятиугольными и квадратной, 5 — пятиугольной и двумя квадратными. Имеет 50 рёбер одинаковой длины. 5 рёбер располагаются между пятиугольной и квадратной гранями, 30 рёбер — между пятиугольной и треугольной, остальные 15 — между квадратной и треугольной. У пятискатной прямой куполоротонды 25 вершин. В 10 вершинах сходятся две пятиугольных и две треугольных грани; в 5 вершинах — пятиугольная, две квадратных и треугольная; в остальных 10 — пятиугольная, квадратная и две треугольных. Пятискатную прямую куполоротонду можно получить из двух других многогранников Джонсона — пятискатного купола (J5) и пятискатной ротонды (J6), — приложив их друг к другу десятиугольными гранями так, чтобы параллельные десятиугольным пятиугольные грани двух многогранников оказались повёрнуты одинаково. Метрические характеристикиЕсли пятискатная прямая куполоротонда имеет ребро длины , её площадь поверхности и объём выражаются как Примечания
Ссылки
|
||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia