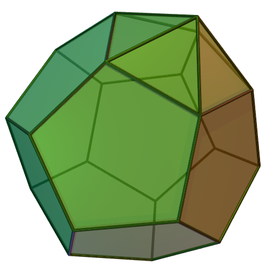
Наращённый додекаэдр

Наращённый додекаэдр
(3D-модель)
Тип	многогранник Джонсона
Свойства	выпуклый
Комбинаторика
Элементы	16 граней 35 рёбер 21 вершина Χ = 2
Грани	5 треугольников 11 пятиугольников
Конфигурация вершины	3x5(5^3) 5(3^2.5^2) 1(3^5)
Развёртка
Классификация
Обозначения	J58, М15+М3
Группа симметрии	C5v

Наращённый додека́эдр[1] — один из многогранников Джонсона (J₅₈, по Залгаллеру — М₁₅+М₃).

Составлен из 16 граней: 5 правильных треугольников и 11 правильных пятиугольников. Среди пятиугольных 6 граней окружены пятью пятиугольными, остальные 5 — четырьмя пятиугольными и треугольной; каждая треугольная грань окружена пятиугольной и двумя треугольными.

Имеет 35 рёбер одинаковой длины. 25 рёбер располагаются между двумя пятиугольными гранями, 5 рёбер — между пятиугольной и треугольной, остальные 5 — между двумя треугольными.

У наращённого додекаэдра 21 вершина. В 15 вершинах сходятся три пятиугольных грани; в 5 вершинах сходятся две пятиугольных и две треугольных грани; в 1 вершине сходятся пять треугольных граней.

Наращённый додекаэдр можно получить из двух многогранников — додекаэдра и пятиугольной пирамиды (J₂), — приложив основание пирамиды к одной из граней додекаэдра.

Метрические характеристики

Если наращённый додекаэдр имеет ребро длины ${\displaystyle a}$, его площадь поверхности и объём выражаются как

${\displaystyle S={\frac {1}{4}}\left(5{\sqrt {3}}+11{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}\approx 21{,}0903149a^{2},}$

${\displaystyle V={\frac {1}{24}}\left(95+43{\sqrt {5}}\right)a^{3}\approx 7{,}9646218a^{3}.}$

Примечания

1. Залгаллер В. А. Выпуклые многогранники с правильными гранями / Зап. научн. сем. ЛОМИ, 1967. — Т. 2. — Cтр. 22.

Ссылки

• Weisstein, Eric W. Наращённый додекаэдр (англ.) на сайте Wolfram MathWorld.