Правильний ікосаедр

Правильний ікосаедр
Натисніть тут, щоб подивитися обертання моделі
Тип	Правильний багатогранник, дельтаедр
Властивості	Опуклий, рівносторонній,однорідний, вершинно-транзитивний, гране-транзитивний
Комбінаторика
Елементи	20 граней ({3}); 30 ребер; 12 вершин (5-го степеня).
Грані	20 Правильних трикутників
Характеристика Ейлера	${\displaystyle \chi =\Gamma -{\hbox{P}}+{\hbox{B}}=2}$
Конфігурація вершини	3.3.3.3.3 = 3^5 Кожна вершина оточена 5 трикутниками.
Вершинна фігура	Правильний п'ятикутник з довжиною сторони ${\displaystyle {\frac {1+{\sqrt {5}}}{2}}}$
Класифікація
Позначення	• I або sT (в нотації Конвея^[en] ) • I5 (в нотації Стюарта) • U22 (як однорідний багатогранник) • C25 (в нотації Г. Коксетера) • W4 (в нотації М. Веннінґера)
Символ Шлефлі	${\displaystyle \left\{3,5\right\}}$
Символ Вітгоффа^[en]	5 | 2 3
Діаграма Коксетера-Динкіна	або (o5o3x)
Діаграма Шлегеля
Група симетрії	Ih^[en], H3, [5,3], (*532), порядок 120 (Повна симетрія правильного ікосаедра)
Група обертань	I, [5,3]^+, (532), порядок 60
Двоїстий багатогранник	Правильний додекаедр
Розгортка

Правильний ікоса́едр (від грец. εικοσάς, «двадцять» і грец. —εδρον, «грань», «лице», «основа») — правильний опуклий двадцятигранник, об'ємна геометрична фігура, поверхня якої складена з двадцяти правильних трикутників, є одним з п’яти опуклих правильних багатогранників (тіл Платона).

Ікосаедр складений з 20 правильних трикутних граней.

Має 30 ребер однакової довжини та 12 вершин (у кожній сходяться 5 ребер).

Його символ Шлефлі — ${\displaystyle \left\{3,5\right\}}$. Це означає, що кожна вершина оточена п'ятьма правильними трикутниками; або також це означає для багатогранника, що його грань — правильний трикутник, а вершинна фігура — правильний п'ятикутник. [1] ^:стор.410

Оскільки всі грані правильного ікосаедра правильні трикутники, то цей багатогранник є дельтаедром.

Правильний ікосаедр

Правильний ікосаедр має 31 вісь обертової симетрії:

‒ 6 осей 5-го порядку — проходять через протилежні вершини; (поворот на 72°, 144°, 216° і 288° або 2π/5, 4π/5, 6π/5, 8π/5 радіан);

‒ 10 осей 3-го порядку — проходять через центри протилежних граней; (поворот на 120° і 240° або 2π/3 і 4π/3 радіан);

‒ 15 осей 2-го порядку — проходять через середини протилежних паралельних ребер (поворот на 180° або π радіан).

Правильний ікосаедр має 15 площин дзеркальної симетрії, що проходять через вершину та середину протилежного ребра для кожної грані.

Має центр симетрії (в ньому перетинаються всі осі та площини симетрії).

Сума плоских кутів при кожній з 12 вершин дорівнює 300°.

Правильний ікосаедр має 59 зірчастих форм.

Геометрія

Правильний ікосаедр як двічі нарощена п'ятикутна антипризма

Правильний ікосаедр з довжиною ребра a можна отримати, наростивши правильну п'ятикутну антипризму з довжиною ребра a двома правильними п'ятикутними пірамідами з довжиною ребра a (що є багатогранниками Джонсона J₂). При цьому висота нарощених пірамід дорівнює ${\displaystyle OH={\sqrt {\tfrac {5-{\sqrt {5}}}{10}}}\cdot a={\tfrac {1}{\sqrt {\varphi +2}}}\cdot a\approx 0.525731\cdot a}$

Таким чином правильний ікосаедр також можна назвати скрученою подовженою п'ятикутною біпірамідою.[2] В цьому випадку він має діедричну симетрію 5-Антипризми (D_5d^[en], [2^+,10], (2*5), порядок 20).

Багатогранник Каталана (Триакісікосаедр)	Зірчастий багатогранник

Наростивши на всіх гранях правильного ікосаедра з довжиною ребра a прямі трикутні піраміди, висотою ${\displaystyle {\frac {5{\sqrt {15}}-9{\sqrt {3}}}{66}}\cdot a\approx 0.05721908\cdot a}$, отримаємо напівправильний рівнокутний багатогранник Каталана — триакісікосаедр.

Якщо висота нарощених пірамід буде дорівнювати ${\displaystyle {\frac {\sqrt {3}}{6}}(3+{\sqrt {5}})\cdot a={\sqrt {\frac {7+3{\sqrt {5}}}{6}}}\cdot a\approx 1.5115226\cdot a}$ [3], то отримаємо зірчастий багатогранник, що є топологічно еквівалентним до триакісікосаедра і візуально схожий на великий зірчастий додекаедр (одне з тіл Кеплера — Пуансо).

Якщо на гранях правильного ікосаедра прямі трикутні піраміди, висотою ${\displaystyle {\frac {\sqrt {3}}{6}}(3-{\sqrt {5}})\cdot a\approx 0.22052818\cdot a}$ [3], наростити в тіло багатогранника (тобто фактично видалити з нього), то отримаємо зірчастий багатогранник, що є топологічно еквівалентним до триакісікосаедра і візуально схожий на великий додекаедр (одне з тіл Кеплера — Пуансо).

Властивості

• Всі 12 вершин правильного ікосаедра лежать в чотирьох паралельних площинах.

• Перерізом ікосаедра площиною, перпендикулярною до осей симетрії 5-го порядку (діагоналей правильного ікосаедра), може бути:

1. правильний п'ятикутник ; Найбільший за площею переріз у формі правильного п'ятикутника (проходить через п'ять вершин ікосаедра) ділить діагональ ікосаедра у співвідношенні ${\displaystyle 1:\varphi ^{2}=1:2.61803399}$
2. правильний десятикутник (якщо площина проходить також через центр правильного ікосаедра; таких перерізів ікосаедр має 6) [4] ;
3. напівправильний рівнокутний десятикутник (має два типи ребер, що чергуються між собою).

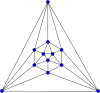
Переріз правильного ікосаедра площиною, що проходить перпендикулярно до осі симетрії 3-го порядку паралельно до його грані і проходить через три вершини ікосаедра, має форму напівправильного рівностороннього шестикутника (з чергуванням двох типів вершин); якщо ця площина також проходить через центр ікосаедра, то переріз має форму напівправильного рівностороннього дванадцятикутника (з чергуванням двох типів вершин).

Анімація складання розгортки правильного ікосаедра

Одна з розгорток правильного ікосаедра.

• Правильний ікосаедр має 43 380 різних розгорток [3] [5] (так само як і правильний додекаедр). Це означає, що існує 43380 способів зробити із ікосаедра пласку розгортку, розрізавши 11 ребер. Інші 19 ребер з'єднують 20 рівносторонніх трикутників розгортки.

• Для того, щоб зафарбувати правильний ікосаедр так, що сусідні грані не матимуть однакового кольору, необхідно принаймні три кольори.

Кількість способів розфарбувати правильний ікосаедр так, щоб всі грані мали різні кольори дорівнює 20!/60 = 40 548 366 802 944 000 : група кольорів є групою перестановок з 20 елементів і має розмір 20!, тоді як порядок чистої обертової симетрії правильного ікосаедра дорівнює 60 (половина від повної симетрії, тобто 120 елементів). [2]

• Найбільш щільне пакування правильних ікосаедрів в просторі (тобто таке, що має найменші пустоти між ними) має щільність 0.836357 . [6]^:Стор.25

Зв'язок з правильним додекаедром

Правильний ікосаедр та правильний додекаедр є взаємно двоїстими багатогранниками. Тобто центри граней правильного ікосаедра є вершинами правильного додекаедра, і навпаки, центри граней правильного додекаедра є вершинами правильного ікосаедра.

Якщо правильний ікосаедр має ребро довжиною 1, то його топологічно двоїстий додекаедр (вершини знаходяться в центрах граней початкового ікосаедра) має ребро довжиною ${\displaystyle {\frac {{\sqrt {5}}+1}{6}}\approx 0.53934466}$, а канонічно двоїстий додекаедр (напіввписані сфери канонічно-двоїстої пари багатогранників збігаються) має ребро довжиною ${\displaystyle {\frac {1}{\varphi }}={\frac {{\sqrt {5}}-1}{2}}\approx 0.61803399}$.

Серед правильних багатогранників як ікосаедр, так і додекаедр являють собою найкраще наближення до сфери. Ікосаедр має найбільше число граней, найбільший двогранний кут і найщільніше притискається до своєї вписаної сфери. З іншого боку, додекаедр має найменший кутовий дефект, найбільший тілесний кут при вершині і максимально заповнює свою описану сферу.

Якщо додекаедр вписано у сферу, то він займає 66.49% об'єму сфери. А ікосаедр, вписаний у ту саму сферу, займає 60.54% її об'єму.

Сфера, що вписана в ікосаедр, охоплює 89,635% його об'єму порівняно з 75,47% для додекаедра.

Об'єм правильного додекаедра з довжиною ребра  більш ніж у три з половиною рази більший за об'єм ікосаедра з такою самою довжиною ребер:

${\displaystyle V_{\text{додек.}}=7.663...\cdot a}$ та ${\displaystyle V_{\text{ікос.}}=2.181...\cdot a}$.

Відношення об'ємів складає:

${\displaystyle {\frac {V_{\text{додек.}}}{V_{\text{ікос.}}}}={\frac {3(5+3{\sqrt {5}})}{10}}={\frac {3}{5}}\cdot (3\varphi +1)=1.8\cdot \varphi +0.6\approx 3.51246117975}$

Додекаедр, вписаний в ікосаедр

Ікосаедр, вписаний в додекаедр

• В правильний ікосаедр можна вписати правильний додекаедр таким чином, що всі 20 вершин додекаедра знаходитимуться в центрах граней ікосаедра.
• Правильний ікосаедр можна вписати в правильний додекаедр таким чином, що всі 12 вершин ікосаедраа будуть розташовані в центрах 12-ти граней додекаедра.

Зв'язок з іншими правильними багатогранниками

Правильний ікосаедр, вписаний в куб.

• В правильний ікосаедр може бути вписаний правильний тетраедр, притому чотири вершини тетраедра будуть суміщені з чотирма вершинами ікосаедра.
• У куб з довжиною ребра ${\textstyle a=1}$ можна вписати правильний ікосаедр з довжиною ребра ${\textstyle {\frac {1}{\varphi }}\approx 0.618}$, так, що шість взаємно паралельних ребер ікосаедра будуть розташовані відповідно на шести гранях куба і лежатимуть паралельно (або перпендикулярно) до ребер куба; решта 24 ребра лежатимуть всередині куба, всі дванадцять вершин ікосаедра лежатимуть на шести гранях куба. [7] ^:Стор.9

Існує 5 різних способів вписати ікосаедр в куб.

Якщо в додекаедр вписано куб, а в куб вписано ікосаедр, то ці додекаедр та ікосаедр мають однакову довжину ребра.

• Ікосаедр можна вписати в октаедр, розмістивши його 12 вершин на 12 ребрах октаедра так, щоб вони розділили кожне ребро у відношенні «золотого перетину». Оскільки золоті перерізи нерівні, існує п'ять різних способів зробити це послідовно, тому в кожен октаедр можна вписати п'ять різних ікосаедрів.

Зв'язок з «золотим прямокутником»

Золоті прямокутники в ікосаедрі.

В правильний ікосаедр ідеально вписуються три взаємно перпендикулярні і відцентровані « золоті прямокутники » з відношенням сторін ${\displaystyle 1:\varphi =1:1.61803399}$, що мають спільну точку в центрі ікосаедра.

При цьому дві короткі сторони одного такого прямокутника збігаються з протилежними паралельними ребрами ікосаедра. [8]^:Стор.71

Формули

У всіх формулах нижче:

${\displaystyle \varphi =2\cdot \cos \left({\frac {\pi }{5}}\right)={\frac {{\sqrt {5}}+1}{2}}\approx 1.618034}$ — відношення пропорції «золотого перетину».

(послідовність A001622 з Онлайн енциклопедії послідовностей цілих чисел, OEIS)

Діагоналі

Кількість діагоналей опуклого багатогранника: ${\displaystyle {\binom {B}{2}}-P}$,

де В — кількість вершин, Р — кількість ребер багатогранника.

Для правильного ікосаедра:

${\displaystyle {\binom {12}{2}}-30={\frac {12}{2}}\cdot {\frac {11}{1}}-30=66-30=36}$ діагоналей.

Всі діагоналі правильного ікосаедра є просторовими; граневих діагоналей він не має.

Діагоналі правильного ікосаедра з довжиною ребра ${\displaystyle a}$
	Просторові діагоналі	${\displaystyle AB={\frac {1+{\sqrt {5}}}{2}}\cdot a=\varphi \cdot a}$	≈ 1.6180339887 ${\displaystyle \cdot a}$
		${\displaystyle AC={\sqrt {\frac {5+{\sqrt {5}}}{2}}}\cdot a={\sqrt {\varphi +2}}\cdot a}$	≈ 1.9021130326 ${\displaystyle \cdot a}$

Метричні характеристики

Для правильного ікосаедра з довжиною ребра ${\displaystyle a}$ [9]
Радіус вписаної сфери (Торкається всіх граней багатогранника)	${\displaystyle r={\frac {\sqrt {3}}{12}}\cdot \left(3+{\sqrt {5}}\right)\cdot a={\frac {\sqrt {3}}{6}}\cdot \varphi ^{2}\cdot a={\frac {\sqrt {3}}{6}}\cdot \left(\varphi +1\right)\cdot a}$	≈ 0.7557613141 ${\displaystyle \cdot a}$ послідовність A179294 з Онлайн енциклопедії послідовностей цілих чисел, OEIS
Радіус напіввписаної сфери (Торкається всіх ребер багатогранника)	${\displaystyle \rho ={\frac {1+{\sqrt {5}}}{4}}\cdot a={\frac {\varphi }{2}}\cdot a}$	≈ 0.8090169944 ${\displaystyle \cdot a}$
Радіус описаної сфери (Містить всі вершини багатогранника)	${\displaystyle R={\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{2}}}\cdot a={\frac {1}{2}}\cdot {\sqrt {\varphi +2}}\cdot a}$	≈ 0.9510565163 ${\displaystyle \cdot a}$ послідовність A179296 з Онлайн енциклопедії послідовностей цілих чисел, OEIS
Висота H (Відстань між паралельними гранями)	${\displaystyle H=2\cdot r={\frac {\sqrt {3}}{6}}\cdot \left(3+{\sqrt {5}}\right)\cdot a={\frac {\sqrt {3}}{3}}\cdot \varphi ^{2}\cdot a}$	≈ 1.5115226281 ${\displaystyle \cdot a}$
Площа поверхні	${\displaystyle S=5\cdot {\sqrt {3}}\cdot a^{2}}$ ${\displaystyle S=30\cdot {\sqrt {3}}\cdot (7-3{\sqrt {5}})\cdot r^{2}={\frac {60\cdot {\sqrt {3}}}{\varphi ^{4}}}\cdot r^{2}}$ ${\displaystyle S=2\cdot {\sqrt {3}}\cdot (5-{\sqrt {5}})\cdot R^{2}=4\cdot {\sqrt {3}}\cdot (3-\varphi )\cdot R^{2}}$	≈ 8.6602540378 ${\displaystyle \cdot a^{2}}$ ≈ 15.1621684308 ${\displaystyle \cdot r^{2}}$ ≈ 9.5745413833 ${\displaystyle \cdot R^{2}}$
Об'єм	${\displaystyle V={\frac {5}{12}}\cdot \left(3+{\sqrt {5}}\right)\cdot a^{3}={\frac {5}{6}}\cdot \varphi ^{2}\cdot a^{3}}$ ${\displaystyle V=10\cdot {\sqrt {3}}\cdot (7-3{\sqrt {5}})\cdot r^{3}={\frac {20\cdot {\sqrt {3}}}{\varphi ^{4}}}\cdot r^{3}}$ ${\displaystyle V={\frac {2}{3}}\cdot {\sqrt {10+2{\sqrt {5}}}}\cdot R^{3}={\frac {4}{3}}\cdot {\sqrt {\varphi +2}}\cdot R^{3}}$	≈ 2.18169499 ${\displaystyle \cdot a^{3}}$ ≈ 5.054056143 ${\displaystyle \cdot r^{3}}$ ≈ 2.53615071 ${\displaystyle \cdot R^{3}}$

Відношення радіусів ${\displaystyle {\frac {R}{r}}={\frac {\sqrt {3\cdot (3-\varphi )}}{\varphi }}={\sqrt {15-6{\sqrt {5}}}}\approx 1.25840857}$  однакове, як для правильного додекаедра, так і для правильного ікосаедра. Таким чином, якщо правильні додекаедр та ікосаедр мають однакові вписані сфери, то їх описані сфери також рівні між собою. Доведення цього математичного результату дано в Началах Евкліда.

Центр масс правильного ікосаедра знаходиться в його геометричному центрі.

Момент інерції суцільного правильного ікосаедра з масою m та довжиною ребра a (вісь обертання проходить через протилежні вершини):[10]

${\displaystyle I={\frac {3+{\sqrt {5}}}{20}}\cdot m\cdot a^{2}={\frac {\varphi ^{2}}{10}}\cdot m\cdot a^{2}\approx 0.26180339887\cdot m\cdot a^{2}}$

Вписана сфера правильного ікосаедра	Напіввписана сфера правильного ікосаедра	Описана сфера правильного ікосаедра

Точка в просторі

Нехай описана сфера ікосаедра має радіус R. Нехай дано довільну точку в просторі і відстані від неї до вершин ікосаедра дорівнюють d_i . Тоді виконується рівність: [11] ^:стор.353, теор.7.2

${\displaystyle {\frac {1}{12}}\sum _{i=1}^{12}d_{i}^{4}+{\frac {16R^{4}}{9}}=\left({\frac {1}{12}}\sum _{i=1}^{12}d_{i}^{2}+{\frac {2R^{2}}{3}}\right)^{2}.}$

Якщо точка знаходиться на описаній сфері ікосаедра, то виконується рівність:[11] ^:стор.354, теор.7.6

${\displaystyle \sum _{i=1}^{12}d_{i}^{2}=9\cdot \sum _{i=1}^{12}d_{i}^{4}}$

Кути

Плоскі кути граней при вершині: 60°.

Сума плоских кутів при кожній з 12 вершин дорівнює 300°.

Кути багатогранника
Кут, під яким ребро видно з центру правильного ікосаедра	${\displaystyle \delta =\arccos \left({\frac {\sqrt {5}}{5}}\right)=2\cdot \arcsin \left({\frac {1}{\sqrt {\varphi +2}}}\right)=2\cdot \arctan \left({\frac {1}{\varphi }}\right)}$	≈ 1.10714871779 рад ≈ 63°26′ 5.81576′′
Двогранний кут між гранями [9]^:Стор.8	${\displaystyle \theta =\arccos \left(-{\frac {\sqrt {5}}{3}}\right)=2\cdot \arcsin \left({\frac {\varphi }{\sqrt {3}}}\right)=2\cdot \arctan \left(\varphi +1\right)}$	≈ 2.4118649973 рад ≈ 138°11′ 22.866375′′
Тілесний кут при вершині	${\displaystyle \Omega _{1}=2\pi -5\cdot \arcsin \left({\frac {2}{3}}\right)=2\pi -5\cdot \arctan \left({\frac {2}{\sqrt {5}}}\right)}$	${\displaystyle \Omega _{1}}$ ≈ 2.63454702604 ср
Тілесний кут, під яким грань видно з центру багатогранника	${\displaystyle \Omega _{2}={\frac {\pi }{5}}}$	${\displaystyle \Omega _{2}}$ ≈ 0.6283185307 ср
Сферичність	${\displaystyle \Psi ={\frac {1}{\sqrt {3}}}\cdot {\sqrt[{3}]{{\frac {\pi }{10}}\cdot (7+3{\sqrt {5}})}}}$	${\displaystyle \Psi \thickapprox 0.93932565}$

Декартові координати вершин

Правильний ікосаедр в декартовій системі координат

Декартові координати 12-и вершин правильного ікосаедра з довжиною ребра ${\displaystyle a=1}$, центр якого знаходиться в початку координат

• ${\displaystyle \left(0,0,\pm {\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{2}}}\right);}$
• ${\displaystyle \left(-{\sqrt {\frac {5+{\sqrt {5}}}{10}}},0,-{\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right),}$ ${\displaystyle \left({\frac {1}{2}}\cdot {\sqrt {\frac {5+2{\sqrt {5}}}{5}}},\pm {\frac {1}{2}},-{\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right),}$ ${\displaystyle \left(-{\frac {1}{2}}\cdot {\sqrt {\frac {5-{\sqrt {5}}}{10}}},\pm {\frac {{\sqrt {5}}+1}{4}},-{\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right);}$
• ${\displaystyle \left({\sqrt {\frac {5+{\sqrt {5}}}{10}}},0,{\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right),}$ ${\displaystyle \left(-{\frac {1}{2}}\cdot {\sqrt {\frac {5+2{\sqrt {5}}}{5}}},\pm {\frac {1}{2}},{\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right),}$ ${\displaystyle \left({\frac {1}{2}}\cdot {\sqrt {\frac {5-{\sqrt {5}}}{10}}},\pm {\frac {{\sqrt {5}}+1}{4}},{\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right).}$

При цьому вершини (окрім двох діаметрально протилежних вершин на осі Oz) лежать в двох паралельних площинах (паралельних до площини Oxy), в кожній з яких розташовані як вершини правильного п'ятикутника.

Початок координат збігається з центром багатогранника, що є його центром симетрії та центром вписаної, напіввписаної та описаної сфер.

Вісь Oz збігається з однією з осей симетрії 5-го порядку, а вісь Oy — з однією з осей симетрії 2-го порядку.

Площина Oxz є однією з площин симетрії багатогранника.

Правильний ікосаедраедр з довжиною ребра ${\displaystyle a=1}$ в декартовій системі координат має вершини з наступними координатами:

• ${\displaystyle \left(-{\frac {\sqrt {3}}{3}},0,{\frac {1}{2}}\cdot {\sqrt {\frac {7+3{\sqrt {5}}}{6}}}\right),}$ ${\displaystyle \left({\frac {\sqrt {3}}{6}},\pm {\frac {1}{2}},{\frac {1}{2}}\cdot {\sqrt {\frac {7+3{\sqrt {5}}}{6}}}\right);}$

• ${\displaystyle \left({\sqrt {\frac {3+{\sqrt {5}}}{6}}},0,{\frac {1}{2}}\cdot {\sqrt {\frac {3-{\sqrt {5}}}{6}}}\right),}$ ${\displaystyle \left(-{\frac {1}{2}}\cdot {\sqrt {\frac {3+{\sqrt {5}}}{6}}},\pm {\frac {1+{\sqrt {5}}}{4}},{\frac {1}{2}}\cdot {\sqrt {\frac {3-{\sqrt {5}}}{6}}}\right);}$
• ${\displaystyle \left(-{\sqrt {\frac {3+{\sqrt {5}}}{6}}},0,-{\frac {1}{2}}\cdot {\sqrt {\frac {3-{\sqrt {5}}}{6}}}\right),}$ ${\displaystyle \left({\frac {1}{2}}\cdot {\sqrt {\frac {3+{\sqrt {5}}}{6}}},\pm {\frac {1+{\sqrt {5}}}{4}},-{\frac {1}{2}}\cdot {\sqrt {\frac {3-{\sqrt {5}}}{6}}}\right);}$
• ${\displaystyle \left({\frac {\sqrt {3}}{3}},0,-{\frac {1}{2}}\cdot {\sqrt {\frac {7+3{\sqrt {5}}}{6}}}\right),}$ ${\displaystyle \left(-{\frac {\sqrt {3}}{6}},\pm {\frac {1}{2}},-{\frac {1}{2}}\cdot {\sqrt {\frac {7+3{\sqrt {5}}}{6}}}\right).}$

При цьому вершини лежать в чотирьох паралельних площинах (паралельних до площини Oxy), в кожній з яких розташовані як вершини правильного трикутника.

Початок координат збігається з центром багатогранника, що є його центром симетрії та центром вписаної, напіввписаної та описаної сфер.

Вісь Oz збігається з однією з осей симетрії 3-го порядку, а вісь Oy — з однією з осей симетрії 2-го порядку.

Площина Oxz збігається з однією з площин симетрії багатогранника.

Золоті прямокутники в ікосаедрі

Вершини ікосаедра з довжиною ребра 2 і центром в початку координат визначають такі декартові координати:

${\displaystyle (0,\pm 1,\pm \varphi )}$ ;

${\displaystyle (\pm 1,\pm \varphi ,0)}$ ;

${\displaystyle (\pm \varphi ,0,\pm 1)}$ .

де ${\displaystyle \varphi ={\frac {{\sqrt {5}}+1}{2}}\approx 1.618034}$ — відношення пропорції «золотого перетину».

При цьому всі вершини лежать в трьох координатних площинах, в кожній з яких розташовані як вершини взаємно відцентрованих і взаємно ортогональних «золотих прямокутників».Осі координат Ox, Oy та Oz збігаються з осями обертової симетрії 2-го порядку, а координатні площини Oxz, Oyz та Oxy є площинами дзеркальної симетрії правильного ікосаедра.

Граф правильного ікосаедра

Граф правильного ікосаедра
3-fold symmetry
Вершин	12
Ребер	30
Радіус	3
Діаметр	3
Обхват	3
Автоморфізм	120
Хроматичне число	4
Властивості	Регулярний, планарний, багатогранний, простий, зв'язний, двозв'язний, симетричний Гамільтонів, граф Келі, циклічний , панциклічний, вершинно-транзитивний, реберно-транзитивний, дистанційно-транзитивний, дистанційно-регулярний

В теорії графів граф правильного ікосаедра — це граф з 12 вершинами та 30 ребрами, що має кістяк правильного ікосаедра.[12]

Також він є одним з 5 платонових графів, кістяк якого є багатогранником Платона.

Всі 12 вершин графа мають степінь 5, а отже, граф є графом 5-го степеня (англ. quintic).

Також граф є 3-вершинно-зв'язним, тобто він залишається зв'язним графом навіть після видалення з нього до трьох (включно) вершин.

Спектр графа : ${\displaystyle Spec(G)=(-{\sqrt {5}})^{3}\left(-1\right)^{5}({\sqrt {5}})^{3}5^{1}}$ [13] [14]

Гамільтонові цикли

Гамільтонів цикл графа ікосаедра

Граф правильного ікосаедра є гамільтоновим, та має 2560 різнихгамільтонових циклів .

Гамільтонів цикл — замкнений шлях, що проходить через кожну вершину графа рівно один раз. Гамільтонів шлях між вершинами U, V існує тоді і тільки тоді, коли u и v мають різні кольори в двокольоровому розфарбуванні графа.

Граф правильного ікосаедра не має ейлерових циклів.

Граф правильного ікосаедра повністю еквівалентний до графа великого додекаедра (одного з правильних багатогранників Кеплера — Пуансо), оскільки ці багатогранники мають однакове розташування вершин^[en] та ребер.

Приклад розфарбовки вершин графа ікосаедра.
Показує хроматичне число графа 4.

Приклад розфарбовки ребер графа ікосаедра.
Показує реберне хроматичне число графа 5.

Симетрія правильного ікосаедра

Правильний ікосаедр має повну ікосаедричну симетрію^[en] I_h, групу Коксетера [5,3], порядку 120, з абстактною структурою групи A₅ × Z₂.

Обертова група симетрії I правильного ікосаедра має порядок 60 і ізоморфна до знакозмінної групи з п'яти елементів (групи чергування парних перестановок п'яти елементів — A₅). Ця неабелева проста група є єдиною нетривіальною нормальною підгрупою симетричної групи S₅ з п'яти елементів.

Повна група симетрії ікосаедра (разом з відбиттями) I_h відома як повна ікосаедрична симетрія^[en] має порядок 120. Вона ізоморфна добутку групи обертової симетрії та групи ${\displaystyle Z_{2}}$ другого порядку, яка утворюється при відбитті через центр ікосаедра. Повна ікосаедрична група I_h має обертову групу симетрії I як нормальну підгрупу індекса 2. Отже, I_h = I × Z₂ = A₅× Z₂ , що відповідає елементу (тотожний елемент ,‒ 1), де Z₂ записано мультиплікативно (кратно).

Зауважимо. що групи I_h (повна ікосаедрична група) та S₅ (симетрична група з 5 елементів) обидві мають порядок 120, але не є ізоморфними.

Кожен багатогранник з ікосаедричною симетрією має 60 обертових симетрій (або симетрій, що зберігають орієнтацію) і 60 симетрій, що змінюють орієнтацію (які поєднують обертання і відбиття)

Повна група симетрії I_h є групою Коксетера типу H₃. Її можна зобразити в нотації Коксетера як [5,3] та діаграмою Коксетера — Динкіна .

Елементи ікосаедричної групи симетрії

Сфера групи повної симетрії I_h правильного ікосаедра із фундаментальною областю.

Елементи симетрії правильного ікосаедра.

1) Правильний ікосаедр має 31 вісь обертової симетрії:

‒ 6 осей 5-го порядку з кутами поворотів на 72°, 144°, 216° і 288° (або 2π/5, 4π/5, 6π/5та 8π/5 радіан) — проходять через протилежні вершини; на діаграмі вони показані синім кольором;

Кожна з них проходить через центр O симетрії ікосаедра а, отже, є віссю дзеркально-обертової симетрії 10-го порядку з такими ж кутами поворотів.

Повороти на чотири кути 2π/5, 4π/5, 6π/5 та 8π/5 радіан при шести парах протилежних граней, дають 4∙6 = 24 поворотів цього типу.

‒ 10 осей 3-го порядку з кутами поворотів на 120° і 240° (або 2π/3 і 4π/3 радіан) — проходять через центри протилежних граней (червоний колір);

Кожна з цих осей проходить через центр симетрії ікосаедра, а тому є його віссю дзеркально-обертової симетрії 6-го порядку з такими ж кутами поворотів.

Повороти на два кути 2π/3 і 4π/3 радіан при десяти парах протилежних вершин дають 2∙10 = 20 поворотів цього типу.

‒ 15 осей 2-го порядку з кутом повороту на 180° (або π радіан) — проходять через середини протилежних паралельних ребер (пурпуровий колір).

Ці повороти також є осьовою симетрією ікосаедра.

Поворот на кут π радіан при п’ятнадцяти парах протилежних ребер, дає 1∙15= 15 поворотів цього типу.

Таким чином 24 + 20 + 15 обертів (+ тотожне перетворення) утворює підгрупу з 60 елементів, ізоморфну до знакозмінної групи A₅ (групи чергування парних перестановок п'яти елементів). Це і є група I власних рухів (обертів) правильного ікосаедра.

2) Правильний ікосаедр має 15 площин дзеркальної симетрії, що проходять через вершину та середину протилежного ребра для кожної грані (на цій сфері вони виглядають як блакитні великі кола), які перетинаються під кутами ${\displaystyle \pi /5,\pi /3,\pi /2}$ у визначеному порядку, розбиваючи сферу на 120 трикутних фундаментальних областей.

3) Має центр симетрії (в ньому перетинаються всі осі та площини симетрії).

Вершини правильного ікосаедра знаходяться в точках, що відповідають осям обертання 5-го порядку.

Фелікс Кляйн написав книгу, в якій використав теорію ікосаедричних симетрій для виведення аналітичного розв'язку рівняння 5-го степеня в загальному вигляді.[15]

Характерною особливістю правильного ікосаедра (також і правильного додекаедра) є наявність в нього осей обертової симетрії 5-го порядку, які не дозволені правилами кристалографії [16]^:Стор.41 , тобто в природі не існує кристалів мінералів, що мають форму правильного ікосаедра.

Пов'язані та споріднені багатогранники

Зірчасті форми правильного ікосаедра

Правильний ікосаедр має 59 зірчастих форм^[en], з яких 32 мають повну, а 27 — неповну ікосаедричну симетрію^[en], що довів в 1938 році Гарольд Коксетер спільно з дю Валем^[en], Флезером (H.T. Flather) і Петрі (John Flinders Petrie) із застосуванням правил обмеження, встановлених Дж. Міллером.[17]

Першою зірчастою формою правильного ікосаедра є він сам. При продовженні (розширені) його грані перетинаються, визначаючи області в просторі (див. діаграму ззірчення) і послідовно утворюють наступні зірчасті форми.

Однією з зірчастих форм правильного ікосаедра є правильний зірчастий багатогранник Кеплера — Пуансо ― великий ікосаедр.

Три зірчасті форми правильного ікосаедра є однорідними з'єднаннями багатогранників: однорідне з'єднання п'яти октаедрів^[en], однорідне з'єднання десяти тетраедрів^[en] та однорідне з'єднання п'яти тетраедрів (що має дві хіральні форми).

21 з 59 зірчастих форм правильного ікосаедра

Діаграма ззірчення правильного ікосаедра.[17]^:стор.19, фіг.4.

Гранування

Великий додекаедр, малий зірчастий додекаедр та великий ікосаедр.

Три правильних зірчастих багатогранники Кеплера — Пуансо мають гранування правильного ікосаедра.

Зокрема, малий зірчастий додекаедр, великий додекаедр та великий ікосаедр мають таке ж розташування вершин^[en] як і в правильного ікосаедра. Всі три багатогранники також мають 30 ребер. Окрім того великий додекаедр має таке ж розташування ребер, як і в правильного ікосаедра, але відрізняється гранями: у великого додекаедра — правильні п'ятикутники, що взаємно перетинаються, а в правильного ікосаедра — правильні трикутники.

Відсікання

Чотири правильногранних багатогранники Джонсона можуть бути отримані з правильного ікосаедра шляхом відсікання від нього частин. Точніше, термін відсікання означає видалення однієї або кількох вершин, ребер, граней багатогранника (відсікається у вигляді піраміди або купола), без порушення інших вершин.

• Відсічений ікосаедр (Скручена подовжена п'ятикутна піраміда) (J₁₁) — утворюється з правильного ікосаедра шляхом видалення будь-якої його вершини разом з ребрами та гранями, що її оточують (відсікається п'ятикутна піраміда).
• Двічі косо відсічений ікосаедр (J₆₂) — видаляються дві несусідні і не протилежні вершини ікосаедра (відсікаються дві п'ятикутні піраміди).
• Тричі відсічений ікосаедр (J₆₃) — видаляються три його вершини разом з ребрами та гранями, що їх оточують (відсікаються три п'ятикутні піраміди).

Двічі протилежно відсічений ікосаедр (коли видаляються дві протилежні вершини) являє собою однорідну п'ятикутну антипризму.

Розсічений правильний ікосаедр

При відсіканні двох сусідніх вершин правильного ікосаедра утворюється багатогранник, що має назву розсічений правильний ікосаедр (англ.dissected regular icosahedron^[en]). Він має 10 вершин, 22 ребра та 14 граней (12 правильних трикутників та 2 рівнобічні трапеції). Багатогранник топологічно еквівалентний до клинокорони^[en] (одного з багатогранників Джонсона, J₈₆) і є вершинною фігурою 4D політопа — великої антипризми^[en].[18]

При відсіканні двох протилежних наборів сусідніх вершин (тобто чотирьох вершин двох протилежних паралельних ребер) утворюється двосхилий бікупол, що має 8 вершин, 14 ребер та 8 граней (4 правильних трикутників та 4 рівнобічні трапеції).

Зв'язок із 600-комірником та іншими 4-політопами

Аналогом правильного ікосаедра в чотиривимірному просторі є 600-комірник, один з шести правильних чотиривимірних політопів^[en].

600-комірник має ікосаедричні перерізи двох розмірів, і кожна з його 120 вершин є ікосаедричною пірамідою; правильний ікосаедр є вершинною фігурою 600-комірника.

600-комірник з одиничним радіусом описаної гіперсфери має комірки у вигляді правильного тетраедра з довжиною ребра ${\textstyle {\frac {1}{\varphi }}}$, 20 з яких зустрічаються у кожній вершині, утворюючи ікосаедричну піраміду (4-піраміду з ікосаедром в основі). Таким чином, 600-комірник містить 120 ікосаедрів з довжиною ребра ${\textstyle {\frac {1}{\varphi }}}$.

600-комірник також містить куби та октаедри з одиничною довжиною ребра як внутрішні елементи, утворені хордами з одиничною довжиною ребра.

120-комірник з одиничним радіусом описаної гіперсфери (іншій правильній 4-політоп, який є одночасно двоїстим до 600-комірника і з'єднанням з п'яти 600-комірників) має всі три види вписаних ікосаедрів (у додекаедр, октаедр та куб).

Правильний ікосаедр є коміркою напівправильного 4-політопа — кирпатого 24-комірника.

Додатково

Тривимірна модель правильного ікосаедра

Будова правильного ікосаедра у стереопроєкції.

Багатокутник Петрі^[en] правильного ікосаедра
Просторовими багатокутниками Петрі^[en] правильного ікосаедра є 6 просторових десятикутників.

Див. також

• Двадцятигранник
• Напівікосаедр
• Ікосаедричне число
• Dogic^[en] — головоломка на зразок кубика Рубика у формі правильного ікосаедра.

Примітки

1. H. S. M. Coxeter, 1954.
2. Klitzing, Richard. ike. https://bendwavy.org/klitzing/home.htm (англ.) . {{cite web}}: Зовнішнє посилання в |website= (довідка)
3. Weisstein, Eric W. Regular Icosahedron(англ.) на сайті Wolfram MathWorld.
4. Alan Holden. Shapes, Space, and Symmetry. — Columbia University Press / New York: Dover, 1991. — P. 200. — ISBN 0-231-08323-8.
5. Edkins, Jo (2007). Icosahedron. Solid shapes and their nets (англ.) . Архів оригіналу за 26 грудня 2019.
6. S. Torquato and Y. Jiao., с. 52.
7. Borovik, Alexandre (2006). Coxeter Theory: The Cognitive Aspects. У Davis, Chandler; Ellers, Erich (ред.). The Coxeter Legacy. Providence, Rhode Island: American Mathematical Society. с. 17—43. ISBN 978-0821837221.
8. Peter R. Cromwell, 1997, с. 71.
9. Kenneth J. MacLean, с. 15.
10. Regular icosahedron inertia tensor - Wolfram Alpha. www.wolframalpha.com (англ.) .
11. Meskhishvili, Mamuka (2020). Cyclic Averages of Regular Polygons and Platonic Solids. Communications in Mathematics and Applications. 11: 335—355. arXiv:2010.12340. doi:10.26713/cma.v11i3.1420.
12. Read, R. C.; Wilson, R. J. (1998). An Atlas of Graphs (англ.) . Oxford University Press.
13. Eric Weisstein. Icosahedral Graph. mathworld.wolfram.com (англ.) .
14. Icosahedral Graph. wolframalpha.com (англ.) .
15. Klein, 1884.
16. І.М. Фодчук, О.О. Ткач., с. 108.
17. H. S. M. Coxeter; The Fifty-nine Icosahedra, 1938.
18. John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26) The Grand Antiprism

Література

• H. S. M. Coxeter. Uniform polyhedra / M. S. Longuet-Higgins, J. C. P. Miller // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — The Royal Society, 1954. — Т. 246, № 916. — С. 401—450. — ISSN 0080-4614. — DOI:10.1098/rsta.1954.0003.
• Peter R. Cromwell. Polyhedra. — Cambridge, U.K. ; New York, NY, USA : Cambridge University Press, 1997. — 451 (англ.) с. — ISBN 9-521-55432-2.

• Kenneth J. MacLean. A Mathematical Analysis of the Icosahedron from a Geometric Perspective. — 2019. — С. 15.

• S. Torquato and Y. Jiao. Dense Packings of Polyhedra: Platonic and Archimedean Solids. — Princeton University, Princeton New Jersey 08544, USA, 2009. — С. 52 (англ.). — DOI:10.1103/PhysRevE.80.041104.

• Felix Klein (1884). Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade (нім.) . Leipzig, B.G. Teubner.
  • Felix Klein (1888). Lectrues on the ikosahedron and the solution of equations of the fifth degree (англ.) . Переклад: George Gavin Morrice. Cornell University Library: London : TRUBNER & CO., LUDGATE HILL. с. 294. cu31924059413439.
• І.М. Фодчук, О.О. Ткач. Основи кристалографії: навчальний посібник. — Чернівці : ЧНУ ім. Юрія Федьковича, 2007. — 108 с.
• H. S. M. Coxeter, Patrick du Val, H.T. Flather, J.F. Petrie. The Fifty-nine Icosahedra. — University of Toronto studies, 1938. — P. 1-26. — (mathematical series 6)

Посилання

• Weisstein, Eric W. Regular Icosahedron(англ.) на сайті Wolfram MathWorld.
• Icosahedron(англ.) на сайті Polytope Wiki.
• Icosahedron (англ.) на сайті dmccooey.com.
• Klitzing, Richard. "Ike".
• Quickfur. "The Icosahedron"
• Nan Ma. "Icosahedron {3, 5}"

• Wedd, N. "The icosahedron"
• Hi.gher.Space Wiki Contributors. "Icosahedron"

• Paper Models of Polyhedra [Архівовано 26 лютого 2013 у Wayback Machine.]
  • Paper Icosahedron
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra