Шістнадцятикомірник

Шістнадцятикомірник
Діаграма Шлегеля: проєкція (перспектива) шістнадцятикомірника в тривимірний простір
Тип	Правильний чотиривимірний політоп
Символ Шлефлі	{3,3,4}
Комірок	16
Граней	32
Ребер	24
Вершин	8
Вершинна фігура	Правильний октаедр
Двоїстий політоп	Тесеракт

Проєкція обертового шістнадцятикомірника в тривимірний простір

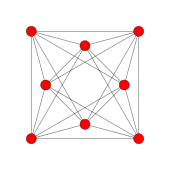
Правильний шістнадцятикомірник, або просто шістнадцятикомірник[1] — один з правильних багатокомірників у чотиривимірному просторі. Відомий також під іншими назвами: гексадекахор (від дав.-гр. ἕξ — «шість», δέκα — «десять» і χώρος — «місце, простір»), чотиривимірний гіпероктаедр (оскільки є аналогом тривимірного октаедра), чотиривимірний кокуб[2] (оскільки двоїстий чотиривимірному гіперкубу), чотиривимірний ортоплекс.

Відкрив Людвіг Шлефлі в середині 1850-х років[3]. Символ Шлефлі шістнадцятикомірника — {3,3,4}.

Опис

Обмежений 16 тривимірними комірками — однаковими правильними тетраедрами. Кут між двома суміжними комірками дорівнює ${\displaystyle 120^{\circ }.}$

Його 32 двовимірні грані — однакові правильні трикутники. Кожна грань розділяє 2 прилеглі до неї комірки.

Має 24 ребра однакової довжини. На кожному ребрі сходяться по 4 грані і по 4 комірки.

Має 8 вершин. У кожній вершині сходяться по 6 ребер, по 12 граней і по 8 комірок. Будь-яка вершина з'єднана ребром з будь-якою іншою — крім вершини, симетричної їй відносно центра багатокомірника.

Шістнадцятикомірник можна уявити як дві однакові правильні чотиривимірні піраміди, прикладені одна до одної своїми октаедричними основами, — або як чотиривимірну дуопіраміду^[en], побудовану на двох квадратах.

В координатах

Шістнадцятикомірник можна розташувати в декартовій системі координат так, щоб його 8 вершини мали координати${\displaystyle (\pm 1;0;0;0),}$${\displaystyle (0;\pm 1;0;0),}$${\displaystyle (0;0;\pm 1;0),}$${\displaystyle (0;0;0;\pm 1).}$

При цьому перерізами багатокомірника 6 координатними площинами будуть 6 квадратів, вершини і ребра яких — відповідно вершини і ребра багатокомірника.

Кожна з 16 комірок багатокомірника буде розташовуватися в одному з 16 ортантів чотиривимірного простору.

Початок координат${\displaystyle (0;0;0;0)}$ буде центром симетрії шістнадцятикомірника, а також центром його вписаної, описаної і напівуписаних тривимірних гіперсфер.

Поверхня шістнадцятикомірника при цьому буде геометричним місцем точок${\displaystyle (x;y;z;w),}$ чиї координати задовольняють рівняння

${\displaystyle |x|+|y|+|z|+|w|=1,}$

а внутрішність багатокомірника — геометричним місцем точок, для яких

${\displaystyle |x|+|y|+|z|+|w|<1.}$

Ортогональні проєкції на площину

Метричні характеристики

Якщо шістнадцятикомірник має ребро довжини ${\displaystyle a,}$ то його чотиривимірний гіпероб'єм і тривимірна гіперплоща поверхні виражаються відповідно як

${\displaystyle V_{4}={\frac {1}{6}}\;a^{4}\approx 0{,}1666667a^{4},}$

${\displaystyle S_{3}={\frac {4{\sqrt {2}}}{3}}\;a^{3}\approx 1{,}8856181a^{3}.}$

Радіус описаної тривимірної гіперсфери (що проходить через усі вершини багатокомірника) в цьому випадку відповідає

${\displaystyle R={\frac {\sqrt {2}}{2}}\;a\approx 0{,}7071068a,}$

радіус зовнішньої напівуписаної гіперсфери (що дотикається до всіх ребер у їх серединах) -

${\displaystyle \rho _{1}={\frac {1}{2}}\;a=0{,}5000000a,}$

радіус внутрішньої напівуписаної гіперсфери (що дотикається до всіх граней у їх центрах) -

${\displaystyle \rho _{2}={\frac {\sqrt {6}}{6}}\;a\approx 0{,}4082483a,}$

радіус вписаної гіперсфери (що дотикається до всіх комірок у їх центрах) -

${\displaystyle r={\frac {\sqrt {2}}{4}}\;a\approx 0{,}3535534a.}$

Заповнення простору

Шістнадцятикомірниками можна замостити чотиривимірний простір без проміжків і накладень.

Примітки

1. Д. К. Бобылёв. Четырехмерное пространство // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп. т.). — СПб., 1890—1907. (рос. дореф.)
2. Е. Ю. Смирнов. Группы отражений и правильные многогранники. [Архівовано 27 січня 2021 у Wayback Machine.] — М.: МЦНМО, 2009. — С. 44.
3. George Olshevsky. Hexadecachoron // Glossary for Hyperspace.

Посилання