Центровані багатокутні числа

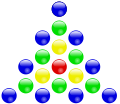
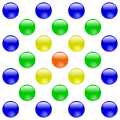
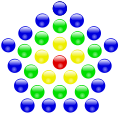
Центровані багатокутні числа — це клас плоских ${\displaystyle k}$-кутних фігурних чисел (${\displaystyle k\geqslant 3}$), одержуваних такою геометричною побудовою. Спочатку на площині фіксується певна центральна точка. Потім навколо неї будується правильний ${\displaystyle k}$-кутник з ${\displaystyle k}$ точками вершин, кожна сторона містить дві точки (див. малюнок). Далі зовні будуються нові шари ${\displaystyle k}$-кутників, причому кожна їхня сторона на новому шарі містить на одну точку більше, ніж у попередньому шарі, тобто, починаючи з другого шару, кожен наступний шар містить на ${\displaystyle k}$ більше точок, ніж попередній. Загальне число точок усередині кожного шару і приймається за центроване багатокутне число (точка в центрі вважається початковим шаром)[1].

Приклади побудови центрованих багатокутних чисел:

Трикутні	Квадратні	П'ятикутні	Шестикутні

З побудови видно, що центровані багатокутні числа виходять як часткові суми такого ряду: ${\displaystyle 1+k+2k+3k+4k+\dots }$ (наприклад, центровані квадратні числа, для яких ${\displaystyle k=4,}$ утворюють послідовність: ${\displaystyle 1,5,13,25,41\dots }$) Цей ряд можна записати як ${\displaystyle 1+k(1+2+3+4+\dots ).}$, звідки видно, що в дужках — породжувальний ряд класичних трикутних чисел. Отже, кожну послідовність центрованих ${\displaystyle k}$-кутних чисел, починаючи з 2-го елементу, можна подати як ${\displaystyle kT_{n}+1,}$ де ${\displaystyle T_{n}(n=1,2,3\dots )}$ — послідовність трикутних чисел. Наприклад, центровані квадратні числа — це помножені на 4 трикутні числа плюс 1, породжувальний ряд для них має вигляд: ${\displaystyle 1+4+8+12\dots }$[2]

Загальна формула для ${\displaystyle n}$-го центрованого ${\displaystyle k}$-кутного числа ${\displaystyle C_{n}^{(k)}}$:

${\displaystyle C_{n}^{(k)}=1+k{\frac {n(n-1)}{2}}={\frac {kn^{2}-kn+2}{2}};\ n=1,2,3\dots }$

({{{3}}})

Зведена таблиця

Число кутів k	Тип числа	Початок послідовності	Посилання на OEIS
3	Центровані трикутні числа	1, 4, 10, 19, 31, …	A005448
4	Центровані квадратні числа	1, 5, 13, 25, 41, …	A001844
5	Центровані п'ятикутні числа	1, 6, 16, 31, 51, …	A005891
6	Центровані шестикутні числа	1, 7, 19, 37, 61, …	A003215
7	Центровані семикутні числа	1, 8, 22, 43, 71, …	A069099
8	Центровані восьмикутні числа	1, 9, 25, 49, 81, …	A016754
9	Центровані дев'ятикутні числа	1, 10, 28, 55, 91, …	A060544
10	Центровані десятикутні числа	1, 11, 31, 61, 101, …	A062786

і так далі.

Примітки

1. Деза Е., Деза М., 2016, с. 39—40.
2. Деза Е., Деза М., 2016, с. 40—41.

Література

• Виленкин Н. Я., Шибасов Л. П. Шибасова 3. Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия. — М. : Просвещение, 1996. — С. 30. — ISBN 5-09-006575-6.
• Глейзер Г. И. [1] — М. : Просвещение, 1964. — 376 с. Архівовано з джерела 4 грудня 2017
• Деза Е., Деза М. Фигурные числа. — М. : МЦНМО, 2016. — 349 с. — ISBN 978-5-4439-2400-7.

Посилання

• Weisstein, Eric W. Центроване багатокутне число(англ.) на сайті Wolfram MathWorld.
• Фігурні числа [Архівовано 23 листопада 2018 у Wayback Machine.] (рос.)