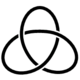
Хіральний вузол

В теорії вузлів хіральний вузол — це вузол, який не еквівалентний своєму дзеркальному відображенню. Орієнтований вузол, еквівалентний своєму дзеркальному відображенню, називається амфіхіральним вузлом або ахіральним вузлом. Хіральність вузла є інваріантом вузла. Хіральність вузлів можна далі класифікувати в залежності від того, оборотний він чи ні.

Існує лише 5 типів симетрій вузлів, які визначаються хіральністю і оборотністю — повністю хіральний, оборотний, додатно амфіхіральний незворотний, від'ємно амфіхіральний незворотний і повністю амфіхіральний оборотний[1].

Історія питання

Хіральність деяких вузлів давно припускалась і доведена Максом Деном 1914 року. П. Г. Тет висловив гіпотезу, що всі амфіхіральні вузли мають парне число перетинів, але Морвен Тіслвейт^[en] 1998 року знайшов контрприклад[2]. Однак гіпотеза Тета доведена для простих альтернованих вузлів[3].

Число вузлів кожного виду хіральності для кожного числа перетинів

Число перетинів	3	4	5	6	7	8	9	10	11	12	13	14	15	16	OEIS sequence
Хіральні вузли	1	0	2	2	7	16	49	152	552	2118	9988	46698	253292	1387166	N / A
Двосторонні вузли	1	0	2	2	7	16	47	125	365	1015	3069	8813	26712	78717	A051769
Повністю хіральні вузли	0	0	0	0	0	0	2	27	187	1103	6919	37885	226580	1308449	A051766
Амфіхіральні вузли	0	1	0	1	0	5	0	13	0	58	0	274	1	1539	A052401
Додатно амфіхіральні вузли	0	0	0	0	0	0	0	0	0	1	0	6	0	65	A051767
Від'ємно амфіхіральні вузли	0	0	0	0	0	1	0	6	0	40	0	227	1	1361	A051768
Повністю амфіхіральніе вузли	0	1	0	1	0	4	0	7	0	17	0	41	0	113	A052400

• Обидва можливих трилисники.
• 
  Лівий трилисник.
• 
  Правий трилисник.

Найпростіший хіральний вузол — трилисник, хіральність якого показав Макс Ден. Всі торичні вузли хіральні. Многочлен Александера не може визначити хіральність вузла, а ось многочлен Джонса в деяких випадках може. Якщо V _k (q) ≠ V _k (q ^−1), то вузол хіральний, проте зворотне не обов'язково істинне. Многочлен HOMFLY ще краще розпізнає хіральність, але поки не відомо поліноміального інваріанта вузла, який би повністю визначав хіральність[4].

Двосторонній вузол

Оборотний хіральний вузол називається двостороннім. Один з прикладів двосторонніх вузлів — трилисник.

Повністю хіральний вузол

Якщо вузол не еквівалентний ні своєму оберненому, ні своєму дзеркальному образу, він називається повністю хіральним; приклад — вузол 9 32[5].

Амфіхіральний вузол

Вісімка є найпростішим амфіхіральним вузлом.

Амфіхіральний вузол— це вузол, який має автогомеоморфізм α 3-сфери, який обертає орієнтацію і фіксує вузол як множину.

Всі амфіхіральні альтерновані вузли мають парне число перетинів . Перший амфіхіральний вузол з непарним числом перетинів, а саме з 15 перетинами, знайшов Хосте (Hoste) та ін.[3]

Повна амфіхіральність

Якщо вузол ізотопний своєму оберненому і своєму дзеркальному образу, його називають повністю амфіхіральним. Найпростішим вузлом з цією властивістю є вісімка.

Додатна амфіхіральність

Якщо автогомеоморфізм α зберігає орієнтацію вузла, кажуть про додатну амфіхіральність. Це еквівалентно ізотопності вузла своєму дзеркальному відображенню. Жоден із вузлів з числом перетинів меншим від дванадцяти не є додатно амфіхіральним[5].

Від'ємна амфіхіральність

Перший від'ємно амфіхіральний вузол.

Якщо автогомеоморфізм α обертає орієнтацію вузла, кажуть про від'ємну амфіхіральність. Це еквівалентно ізотопності вузла оберненому дзеркальному відображенню. Вузол з цією властивістю з найменшим числом перетинів — це 8₁₇[5].

Примітки

1. Hoste, Thistlethwaite, Weeks, 1998, с. 33—48.
2. Jablan, Slavik & Sazdanovic, Radmila. «History of Knot Theory and Certain Applications of Knots and Links [Архівовано 20 серпня 2011 у Wayback Machine.]», LinKnot.
3. Weisstein, Eric W. Amphichiral Knot(англ.) на сайті Wolfram MathWorld. Accessed: May 5, 2013.
4. «Chirality of Knots 9₄₂ and 10₇₁ and Chern-Simons Theory» by P. Ramadevi, T. R. Govindarajan, and R. K. Kaul. Архів оригіналу за 1 березня 2020. Процитовано 1 березня 2020.
5. Three Dimensional Invariants [Архівовано 17 лютого 2020 у Wayback Machine.] Knot Atlas

Література

• Jim Hoste, Morwen Thistlethwaite, Jeff Weeks. The first 1,701,936 knots // The Mathematical Intelligencer. — 1998. — Т. 20, вип. 4. — DOI:10.1007/BF03025227. Архівовано з джерела 15 грудня 2013.