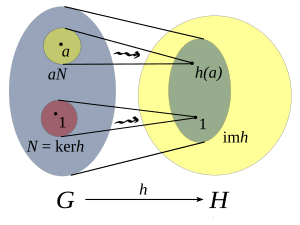
 从
从 (左)到
(左)到 (右)的群同态(
(右)的群同态( )的像。在
)的像。在 内的椭圆形是
内的椭圆形是 的像。
的像。 是
是 的核而
的核而 是
是 的陪集。
的陪集。
在数学中,给定两个群 和
和 ,从
,从  到
到  的群同态(Group homomorphism)是函数
的群同态(Group homomorphism)是函数 使得对于所有
使得对于所有 中的
中的 和
和 下述等式成立
下述等式成立

在这里,等号左侧的群运算 ,是
,是 中的运算;而右侧的运算
中的运算;而右侧的运算 是
是 中的运算。
中的运算。
从这个性质,可推导出 将
将 的单位元
的单位元 映射到
映射到 的單位元
的單位元 ,并且它还在
,并且它还在 的意义上映射逆元到逆元。因此我们可以说
的意义上映射逆元到逆元。因此我们可以说 “兼容于群结构”。
“兼容于群结构”。
过去同态 常用
常用 或
或 来表示,它容易混淆于索引或一般下标。更新近的倾向是把群同态写在它们的自变量的右侧,省略括号,如此
来表示,它容易混淆于索引或一般下标。更新近的倾向是把群同态写在它们的自变量的右侧,省略括号,如此 簡化成了
簡化成了 。这种方法因为其更适应自动机从左至右读字的习惯从而在某些广泛应用自动机理论的群论中颇为流行。
。这种方法因为其更适应自动机从左至右读字的习惯从而在某些广泛应用自动机理论的群论中颇为流行。
在考虑有额外的结构的群的数学领域中,同态不仅要满足上述的群结构,还要满足额外的结构。比如拓扑群的同态经常要求是连续的。
像与核
我们定义 的核被映射到
的核被映射到 中单位元
中单位元 上的
上的 中元素的集合
中元素的集合

定义 的像为
的像为

核是 的正规子群(事实上,
的正规子群(事实上, ),而像则是
),而像则是 的子群。同态
的子群。同态 是单射(并叫做单同态)当且仅当
是单射(并叫做单同态)当且仅当 。
。
同态的核和像可以被解释为对它接近于同构的程度。第一同构定理说明了群同态的像 同构于商群
同构于商群 。
。
例子
- 考虑带有加法的循环群
 和整数集
和整数集 的群。映射
的群。映射 ,有
,有 为
为 模以3,是群同态。它是滿射并且它的核由被三整除的所有整数构成。
模以3,是群同态。它是滿射并且它的核由被三整除的所有整数构成。
- 指数映射产生从带有加法的实数集
 的群到带有乘法的非零实数集
的群到带有乘法的非零实数集 的群的群同態。核是
的群的群同態。核是 而像由正实数组成。
而像由正实数组成。
- 指数映射还产生从带有加法的复数集
 的群到带有乘法的非零复数集
的群到带有乘法的非零复数集 的群的同态。这个映射是满射并且有核
的群的同态。这个映射是满射并且有核 ,这可以从欧拉公式得出。
,这可以从欧拉公式得出。
- 给定任何两个群
 和
和 ,映射
,映射 ,把所有
,把所有 的元素对应到
的元素对应到 的单位元,是同态;它的核是集合
的单位元,是同态;它的核是集合 。
。
- 给定任何群
 ,恒等映射
,恒等映射 定义为对于
定义为对于 中所有的
中所有的 ,
, 。恒等映射是群同态。
。恒等映射是群同态。
群范畴
如果 和
和 是群同态,则
是群同态,则 也是群同态。这证明所有群构成的类,和态射即群同态,一起构成一个范畴。
也是群同态。这证明所有群构成的类,和态射即群同态,一起构成一个范畴。
同态映射的类型
如果同态 是双射,则你还可以证明它的逆映射仍是同态,这种
是双射,则你还可以证明它的逆映射仍是同态,这种 叫做群同构;在这种情况下,群
叫做群同构;在这种情况下,群 和
和 被称为是“同构的”:它们只在元素的符号上有差异而对于所有实践用途都是同一的。
被称为是“同构的”:它们只在元素的符号上有差异而对于所有实践用途都是同一的。
如果 是群同态,我们称之为
是群同态,我们称之为 的自同态。如果它进一步的是双射并且因此是同构,则称为自同构。群
的自同态。如果它进一步的是双射并且因此是同构,则称为自同构。群 的所有自同构的集合,带有函数复合作为运算,自身形成一个群,叫做
的所有自同构的集合,带有函数复合作为运算,自身形成一个群,叫做 的自同构群,记为
的自同构群,记为 。例如说,
。例如说, 的自同构群只有两个元素,恒等变换和乘以
的自同构群只有两个元素,恒等变换和乘以 ;它同构于
;它同构于 。
。
满同态是满射的同态,单同态是单射的同态。
阿贝尔群的同态
如果 和
和 是阿贝尔群(就是交换群),则所有从
是阿贝尔群(就是交换群),则所有从 到
到 的群同态的集合
的群同态的集合 自身是阿贝尔群:两个同态的和
自身是阿贝尔群:两个同态的和 定义为
定义为
- 对于所有
 中
中 ,
, 。
。
 的交换律对于证明
的交换律对于证明 也是群同态是必需的。同态的加法在如下意义上兼容于同态的复合:如果
也是群同态是必需的。同态的加法在如下意义上兼容于同态的复合:如果 在
在 中,
中, ,
,  是
是 的元素,并且
的元素,并且 在
在 中,则
中,则
 ,并且
,并且 。
。
这证明了一个阿贝尔群的所有自同态的集合 形成了一个环,即
形成了一个环,即 的自同态环。例如,由两个
的自同态环。例如,由两个 的直积构成的阿贝尔群(克莱因四元群)的自同态群同构于带有
的直积构成的阿贝尔群(克莱因四元群)的自同态群同构于带有 内元素的
内元素的 矩阵的环。上述兼容性还证明所有阿贝尔群带有群同态的范畴形成了预加法范畴;存在直积和良定义的核使这个范畴成为阿贝尔范畴的原型。
矩阵的环。上述兼容性还证明所有阿贝尔群带有群同态的范畴形成了预加法范畴;存在直积和良定义的核使这个范畴成为阿贝尔范畴的原型。
参见
引用
- Lang, Serge, Algebra, Graduate Texts in Mathematics 211 3rd, Springer-Verlag, 2002 .
外部連結




























































