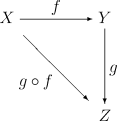| 此條目需要 精通或熟悉相关主题的编者参与及协助编辑。 (2011年12月11日)
請邀請適合的人士改善本条目。更多的細節與詳情請參见討論頁。 |
态射(英語:Morphism)在数学中是指两个数学结构之间保持结构的一种映射。
许多当代数学领域中都有态射的身影。例如,在集合论中,态射就是函数;在群论中,它们是群同态;而在拓扑学中,它们是连续函数;在泛代数(universal algebra)的范围,态射通常就是同态。
对态射和它们定义于其间的结构(或对象)的抽象研究构成了范畴论的一部分。在范畴论中,态射不必是函数,而通常被视为两个对象(不必是集合)间的箭头。不像映射一个集合的元素到另外一个集合,它们只是表示域(domain)和陪域(codomain)间的某种关系。
尽管态射的本质是抽象的,多数人关于它们的直观(事实上包括大部分术语)来自于具体范畴的例子,在那里对象就是有附加结构的集合而态射就是保持这种结构的函数。
定义
一个范畴C由两个类给定:一个对象的类和一个态射的类。
有两个操作定义在每个态射上,域(domain,或源)和陪域(codomain,或目标)。
态射经常用从域到他们的陪域的箭头来表示,例如若一个态射f域为X而陪域为Y,它记为f : X → Y。所有从X到Y的态射的集合记为homC(X,Y)或者hom(X, Y)。(有些作者采用MorC(X,Y)或Mor(X, Y))。
对于任意三个对象X,Y,Z,存在一个二元运算hom(X, Y)×hom(Y, Z) → hom(X, Z)称为复合。f : X → Y和g : Y → Z的复合记为 或gf(有些作者采用fg)。态射的复合经常采用交换图来表示。例如
或gf(有些作者采用fg)。态射的复合经常采用交换图来表示。例如
态射必须满足两条公理:
- 存在恒等态射:对于每个对象X,存在一个态射idX : X → X称为X上的恒等态射,使得对于每个态射f : A → B我们有
 。
。
- 满足结合律:
 在任何操作有定义的时候。
在任何操作有定义的时候。
当C是一个具体范畴的时候,复合只是通常的函数复合,恒等态射只是恒等函数,而结合律是自动满足的。(函数复合是结合的。)
注意域和陪域本身是决定态射的信息的一部分。例如,在集合的范畴,其中态射是函数,两个函数可以作为有序对的集合相等,但却有不同的陪域。这些函数从范畴论的目的来说被视为不同。因此,很多作者要求态射类hom(X, Y)是不交的。实际上,这不是一个问题,因为如果他们不是不交的,域和陪域可以加到态射上,(例如,作为一个有序三元组的第二和第三个分量),使得它们不交(互斥,disjoint)。
态射的类型
- 同构(isomorphism):令f : X → Y为一个态射。若存在态射g : Y → X使得
 和
和 成立,则f称为一个同构。g称为f的逆态射,逆态射g如果存在就是唯一的,而且显而易见g也是一个同构,其逆为f。两个对象之间有一个同构,那么这两个对象称为同构的或者等价的。同构是范畴论中态射的最重要种类。[1][2]
成立,则f称为一个同构。g称为f的逆态射,逆态射g如果存在就是唯一的,而且显而易见g也是一个同构,其逆为f。两个对象之间有一个同构,那么这两个对象称为同构的或者等价的。同构是范畴论中态射的最重要种类。[1][2]
- 满同态(epimorphism):令态射f : X → Y,如果对于所有Y → Z的态射g1,g2有
 ,称态射f为满同态。这也称为epi或epic.具体范畴中的满同态通常是满射(surjective)函数,虽然并不总是这样。[3][2]
,称态射f为满同态。这也称为epi或epic.具体范畴中的满同态通常是满射(surjective)函数,虽然并不总是这样。[3][2]
- 单同态(monomorphism):令态射f : X → Y,如果对于所有Z → X的态射g1,g2,
 成立,则称f为单同态。它也称为mono或者monic.具体范畴中的单同态通常为单射(injective)函数。[4][2]
成立,则称f为单同态。它也称为mono或者monic.具体范畴中的单同态通常为单射(injective)函数。[4][2]
- 双同态(bimorphism):若f既是满同态也是单同态,则称f为双同态(bimorphism)。
注意每个同构都是双同态,但不是每个双同态都是同构。例如,交换环的范畴中,包含映射Z → Q是一个双同态,但不是一个同构。如果在一个范畴中每个双同态都是同构,则这个范畴称为一个平衡范畴。例如,集合是一个平衡范畴。
- 自同态(endomorphism):任何态射f : X → X称为X上的一个自同态。
- 自同构(automorphism):若一个自同态也是同构的,那么称之为自同构。
- 若f : X → Y和g : Y → X满足
 可是证明f是满的而g是单的,而且
可是证明f是满的而g是单的,而且 : X → X是幂等的。这种情况下,f和g称为分割(split). f称为g的收缩(retraction)而g称为f的截面。任何既是满同态又是分割单同态的态射,或者既是单同态又是分割满同态的态射必须是同构。
: X → X是幂等的。这种情况下,f和g称为分割(split). f称为g的收缩(retraction)而g称为f的截面。任何既是满同态又是分割单同态的态射,或者既是单同态又是分割满同态的态射必须是同构。
例子
更多的例子参看范畴论条目。
参看
腳注