円に外接する四角形

円に外接する四角形とその内接円

平面幾何学において、円に外接する四角形[1]（えんにがいせつするしかくけい、英: circumscribed quadrilateral,circumscribable quadrilateral,circumscribing quadrilateral,circumscriptible quadrilateral[2]）または円外接四辺形[3][4]、接線四辺形（英: tangential quadrilateral,tangent quadrilateral）はすべての辺がある円に接する凸四角形である。特にこの円とその中心、半径をそれぞれ内接円、内心、内半径という。円に外接する四角形は円外接多角形の一つである。

英語では inscriptable quadrilateral, inscriptible quadrilateral, inscribable quadrilateral, circumcyclic quadrilateral,co-cyclic quadrilateralなどと言われる場合もある[2][5]。 しかしこの語は円に内接する四角形を指す場合が多く混同を避けるため、あまり使われない[2]。

任意の三角形は内接円を持つが四角形ではそうとは限らない。例えば、正方形でない長方形は内接円を持たない。 四角形が円に外接する必要十分条件は後述のピトーの定理などがある。

特別な場合

円に外接する四角形の例にひし形、正方形を含む凧形がある。凧形は円に外接する四角形であり、直交対角線四角形でもある[6]。また、直角凧形は外接円を持つ。内接円と外接円を持つ四角形は双心四角形と呼ばれ、直角凧形はその一つである。

円に外接する台形は円に外接する台形と呼ばれる。

特徴づけ

円に外接する四角形の4つの角の二等分線はその内心で交わる。逆に四角形の4つの角の二等分線が共点ならばその四角形は円に外接する四角形である[7]。

ピトーの定理によれば、円に外接する四角形の2組の対辺の長さの和は等しい。またその長さは四角形の半周長である。

${\displaystyle a+c=b+d={\frac {a+b+c+d}{2}}=s.}$

逆に a + c = b + d ならばその四角形は円に外接する[2]:p.65[7]。

図のように台形でない凸四角形ABCDのそれぞれの対辺の交点をE,Fとする。 四角形ABCDが円に外接することと、以下の式が成り立つことは同値である[7]。

${\displaystyle \displaystyle BE+BF=DE+DF\quad \mathrm {or} \quad AE-EC=AF-FC}$

他の、四角形が円に内接する必要十分条件は、△ABC,△ADCの内接円が接することである[2]:p.66。

1954年、Iosifescuは凸四角形が円に外接する必要十分条件を、以下の様な、対角線と辺の成す角による表現でまとめた[8]。

${\displaystyle \tan {\frac {\angle ABD}{2}}\cdot \tan {\frac {\angle BDC}{2}}=\tan {\frac {\angle ADB}{2}}\cdot \tan {\frac {\angle DBC}{2}}.}$

円に外接する四角形（青）とその内接円（破線）と4つの外部で接する円（赤）。赤い円はある2つの辺の延長で接している。

更に、辺長がa,b,c,dである凸四角形が円に外接することは

${\displaystyle R_{a}R_{c}=R_{b}R_{d}}$

と同値である。ここでR_a,R_b,R_c,R_dはそれぞれ辺a,b,c,dとその隣接する辺の延長に接する円の半径である[9]:p.72。

さらなる特徴づけには四角形の辺と対角線が成す4つの三角形を用いるものがある。

接点と接線の長さ

円に外接する四角形（青）とその内接円との接点が成す四角形（緑）。赤い線は緑の四角形の対角線。

円に外接する四角形とその内接円は4点で接する。この4点から成る四角形は接触四角形（contact quadrilateral）とよばれ円に内接する四角形となる。

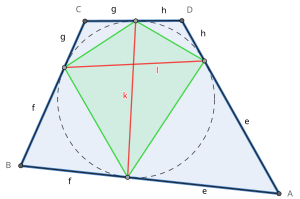
図の様に、4つの接点と対応する各頂点の距離、接線長[10]（tangent lengths）をe,f,g,hとする。内接円と隣り合う2辺の接点と、その間の頂点の距離は等しい。

それぞれ対辺の対辺を結ぶ線分（図ではk,l）はtangency chordsと呼ばれる。これは接触四角形の対角線である。

面積

三角法を用いない公式

円に外接する四角形の面積Kは内半径と半周長を用いて以下の様に表される。

${\displaystyle \displaystyle K=r\cdot s,}$

または、

${\displaystyle \displaystyle K={\tfrac {1}{2}}{\sqrt {p^{2}q^{2}-(ac-bd)^{2}}}}$

ただしp,qは二つの対角線の長さとする[11]。

e,f,g,hを用いれば以下のようになる[6]。

${\displaystyle \displaystyle K={\sqrt {(e+f+g+h)(efg+fgh+ghe+hef)}}.}$

a,b,c,dとe,f,g,hを両方用いれば、

${\displaystyle K={\sqrt {abcd-(eg-fh)^{2}}}.}$

となる[6]:p.128。もしこの四角形が円に内接するならばeg = fhが従い、双心四角形の面積公式${\displaystyle {\sqrt {abcd}}}$となる[12]。

三角法による公式

辺の長さと、三角法を使う公式には以下の様なものがある[13][14][15][16]。

${\displaystyle \displaystyle K={\sqrt {abcd}}\sin {\frac {A+C}{2}}={\sqrt {abcd}}\sin {\frac {B+D}{2}}.}$

円に外接する四角形の辺長が与えられたとき、その面積が最大となるのは、外接円をもつ、つまり双心四角形となるときである。四角形が外接円をもつとき、それぞれの対角の和が180°となるためである。また微分幾何学を用いることによっても証明できる[17]。

四角形の頂点と内心Iの距離を用いたものもある:p.19。

${\displaystyle K=\left(IA\cdot IC+IB\cdot ID\right)\sin {\frac {A+C}{2}}}$

2つの対辺と角によってあらわすこともできる[11]。

${\displaystyle K=ab\sin {\frac {B}{2}}\csc {\frac {D}{2}}\sin {\frac {B+D}{2}}.}$

さらに外積を用いた面積公式ような形の公式もある[11]。

${\displaystyle K={\tfrac {1}{2}}|(ac-bd)\tan {\theta }|,}$

ここでθは対角線の成す角である。ただし凧形ではθは90°であるから上の式を使うことはできない。

不等式

上記の公式から円に外接する四角形の面積Kと辺長a,b,c,dについて

${\displaystyle K\leq {\sqrt {abcd}}}$

が成り立つ。等号成立条件は四角形が双心四角形である場合。

T. A. Ivanova (1976)によれば、内半径と半周長について

${\displaystyle s\geq 4r}$

が成り立つ。等号成立条件は四角形が正方形である場合[18]。 この式とK = rsから

${\displaystyle K\geq 4r^{2}}$

が導かれる。

分割

円に外接する四角形

円に外接する四角形の内接円と各辺の接点と内心を結ぶ線分は四角形を4つの直角凧形に分割する。

円に外接する四角形を、面積と周長の等しい2つの多角形に分ける直線は内心を通る。

内半径

円に外接する四角形ABCDの内半径は面積Kと辺長a,b,c,d、半周長sを用いて以下のように書ける[11]。

${\displaystyle r={\frac {K}{s}}={\frac {K}{a+c}}={\frac {K}{b+d}}}$

円に外接する四角形の辺長が与えられたとき、その内半径が最大値をとるような四角形は双心四角形である。

接線長e,f,g,hを用いれば以下の様にも書ける[12]:Lemma2[19]。

${\displaystyle \displaystyle r={\sqrt {\frac {efg+fgh+ghe+hef}{e+f+g+h}}}.}$

各頂点と内心Iの距離をu = AI, v = BI, x = CI ,y = DIと書けば

${\displaystyle r=2{\sqrt {\frac {(\sigma -uvx)(\sigma -vxy)(\sigma -xyu)(\sigma -yuv)}{uvxy(uv+xy)(ux+vy)(uy+vx)}}}}$

となる[20]。ただし${\displaystyle \sigma ={\tfrac {1}{2}}(uvx+vxy+xyu+yuv)}$

△ABC,△BCD,△CDA,△DABの内半径をそれぞれ${\displaystyle r_{1},r_{2},r_{3},r_{4}}$とすればさらに

${\displaystyle r={\frac {G+{\sqrt {G^{2}-4r_{1}r_{2}r_{3}r_{4}(r_{1}r_{3}+r_{2}r_{4})}}}{2(r_{1}r_{3}+r_{2}r_{4})}}}$

と変形できる[21]。ただし ${\displaystyle G=r_{1}r_{2}r_{3}+r_{2}r_{3}r_{4}+r_{3}r_{4}r_{1}+r_{4}r_{1}r_{2}}$.

角の公式

円に外接する四角形ABCDについて、それぞれの頂点の接線長をe,f,g,hとする。四角形の角に対する正弦は次のように計算できる[6]。

${\displaystyle \sin {\frac {A}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(e+f)(e+g)(e+h)}}},}$

${\displaystyle \sin {\frac {B}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(f+e)(f+g)(f+h)}}},}$

${\displaystyle \sin {\frac {C}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(g+e)(g+f)(g+h)}}},}$

${\displaystyle \sin {\frac {D}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(h+e)(h+f)(h+g)}}}.}$

対辺上の接点を結ぶ直線k,lの成す角の正弦は次のように計算できる[6]。

${\displaystyle \sin {\varphi }={\sqrt {\frac {(e+f+g+h)(efg+fgh+ghe+hef)}{(e+f)(f+g)(g+h)(h+e)}}}.}$

対角線

接線長e,f,g,hを用いて、対角線の長さp = AC , q = BDは以下の様に計算できる[12]:Lemma3。

${\displaystyle \displaystyle p={\sqrt {{\frac {e+g}{f+h}}{\Big (}(e+g)(f+h)+4fh{\Big )}}},}$

${\displaystyle \displaystyle q={\sqrt {{\frac {f+h}{e+g}}{\Big (}(e+g)(f+h)+4eg{\Big )}}}.}$

接点を結ぶ直線

接線長e,f,g,hを用いて、接触四角形の対角線（Tangency chords）の長さk,lは以下の様に計算できる[6]。

${\displaystyle \displaystyle k={\frac {2(efg+fgh+ghe+hef)}{\sqrt {(e+f)(g+h)(e+g)(f+h)}}},}$

${\displaystyle \displaystyle l={\frac {2(efg+fgh+ghe+hef)}{\sqrt {(e+h)(f+g)(e+g)(f+h)}}}}$

ここで四角形の辺の長さa,b,c,dについてa = e + f , c = g + h , b = f + g , d = h + eが成り立つから

${\displaystyle {\frac {k^{2}}{l^{2}}}={\frac {bd}{ac}}.}$

である[6]。2つのTangency chordsには以下の様な性質がある。

• 双心四角形ならば直交する[6]:p.124。
• 凧形ならば長さが等しい[22]:p.166。

円に外接する四角形ABCDについて、AB,CDがBC,DAよりも短ければ、AB,CD間のtangency chordはBC,DA間のtangency chordより長い[23]:p.162。

AB,CDと内接円の接点をそれぞれW,Y、WY,BDの交点をMとする。${\displaystyle {\tfrac {BW}{DY}}}$と${\displaystyle {\tfrac {BM}{DM}}}$は等しい[24]。

共線点

円に外接する四角形（青）のニュートン線 (赤) 。ニュートン線は内心I、対角線の中点M₁,M₂と対辺の交点J,Kを結ぶ線分（緑）の中点M₃を通る。

円に外接する四角形ABCDの対角線AC,BDの中点をそれぞれM₁,M₂、内心をI、対辺AB,CDの交点JとBC,DAの交点Kを通る線分JKの中点をM₃とする。この4点M₁,M₂,M₃,Iは共線である[25][7]:p.42。この線をニュートン線という。

一般に四角形のすべての辺に接する楕円（内接楕円（英語版））の中心は、そのニュートン線上にある[26]。

また接触四角形のそれぞれの対辺の交点をL,Mとすると、J,L,K,Mは共線である[27]:Cor.3。

円に外接する四角形を内心で4つの三角形に分割する。それぞれの垂心（紫）と元の四角形の対角線（緑）の交点は共線である。

AB,BC,CD,DAと内接円の接点をT₁,T₂,T₃,T₄、T₁,T₂,T₃,T₄の等長共役点（AT₁ = BN₁となる点）をそれぞれN₁,N₂,N₃,N₄とする。円に外接する四角形のナーゲル点は直線N₁N₃,N₂N₄ の交点として定義される。N₁N₃,N₂N₄はどちらも四角形の周長を二等分する。さらに四角形のナーゲル点N、質量中心G、内心Iは共線でNG = 2GI が成り立つ。この線はナーゲル線と呼ばれる[28]。

円に外接する四角形ABCDの内心をI、対角線の交点をP、△AIB,△BIC,△CID,△DIAの垂心をそれぞれH_X, H_Y, H_Z, H_WとするとP,H_X, H_Y, H_Z, H_Wは共線である[15]:p.28。

共点と垂線

2つの対角線と2つのtangency chordsは共点である[16][15]:p.11。 これは、ブリアンションの定理で2つの点を極限まで近づけた場合を用いて証明できる。円に外接する六角形の頂点2つを別の頂点に極限まで近づけると、近づかれた2点と、他の2点の接線が円に外接する四角形を成し、近づいた点と近づかれた点の接線の交点はその2点と一致してtangency chordsとなる。同様の操作をすることで、もう一方のtangency chordsの共点も証明できる。

対辺AB,CDの交点JとBC,DAの交点Kを結ぶ直線JKと、対角線の交点Pと内心Iを結ぶ直線IPは直交する[27]:Cor.4。

内心

円に外接する四角形の内心はニュートン線上にある[29]。

内心Iと円に外接する四角形ABCDの頂点の距離の比について次の式が成り立つ[15]:p.15。

${\displaystyle {\frac {AB}{CD}}={\frac {IA\cdot IB}{IC\cdot ID}},\quad \quad {\frac {BC}{DA}}={\frac {IB\cdot IC}{ID\cdot IA}}.}$

この式から、以下の式が満足する[30]。

${\displaystyle AB\cdot BC=IB^{2}+{\frac {IA\cdot IB\cdot IC}{ID}}.}$

また

${\displaystyle IA\cdot IC+IB\cdot ID={\sqrt {AB\cdot BC\cdot CD\cdot DA}}.}$

が成り立つ[15]:p.16。内心が頂点の重心（幾何中心）となるのは、

${\displaystyle IA\cdot IC=IB\cdot ID.}$

が成立することと同値である[15]:p.22。AC,BDの中点をそれぞれM_p,M_qとすると、以下の式が成り立つ[15]:p.19[31]。

${\displaystyle {\frac {IM_{p}}{IM_{q}}}={\frac {IA\cdot IC}{IB\cdot ID}}={\frac {e+g}{f+h}}}$

ただしe,f,g,hはそれぞれA,B,C,Dの接線長である。このことから内心が幾何中心と一致するのは、内心が対角線の中点を繋げた線分の中点であるときである。

円に外接する四角形が四節リンク機構（英語版）とみなすとき、四角形が凸であれば、どのように機構を動かしても、円に外接する状態は変わらない[32][33]。例えば正方形をひし形に変形しても円に外接したままである。ある辺が固定されて四角形が動くとき、その内心は半径が${\displaystyle {\sqrt {abcd}}/s}$の円を描く。ただし、a,b,c,dはいづれかの四角形の辺長で、sは半周長。

4つの三角形の特徴づけ

4つの三角形の内接円半径に関するチャオとシメオノフの特徴づけ

凸四角形ABCDと対角線の交点Pから重なり合わない三角形△APB, △BPC, △CPD, △DPAを作る。四角形が円に外接するときこれらの四角形は多くの特徴を持つ。

△APB, △BPC, △CPD, △DPAの内半径をそれぞれr₁,r₂,r₃,r₄とする。チャオとシメオノフは四角形が円に外接することと次の式の成立が同値であることを証明した[34]。

${\displaystyle {\frac {1}{r_{1}}}+{\frac {1}{r_{3}}}={\frac {1}{r_{2}}}+{\frac {1}{r_{4}}}.}$

ただし、この性質はVaynshtejnが5年早く発表していた[22]:p.169[35]。この問題の解決は、VasilyevとSenderovの証明した性質が使われた。四角形の辺を底辺としてみたときの、4つの三角形の高さをそれぞれh₁,h₂,h₃,h₄とする。四角形が円に外接することと、以下の式が成り立つことは同値である[8][35]。

${\displaystyle {\frac {1}{h_{1}}}+{\frac {1}{h_{3}}}={\frac {1}{h_{2}}}+{\frac {1}{h_{4}}}.}$

内半径と同様に、傍接円半径についても同じような性質がある。△APB, △BPC, △CPD, △DPAの角P内の傍接円の半径をそれぞれr_a,r_b,r_c,r_dとする。四角形が円に外接することと、以下の式が成り立つことは同値である[2]:p.70。

${\displaystyle {\frac {1}{r_{a}}}+{\frac {1}{r_{c}}}={\frac {1}{r_{b}}}+{\frac {1}{r_{d}}}.}$

さらにこれらの三角形の外接円の半径をそれぞれR₁,R₂,R₃,R₄として

${\displaystyle R_{1}+R_{3}=R_{2}+R_{4}.}$

が成り立つことも、四角形が円に外接する必要十分条件となる[36]:pp. 23–24。

1996年、Vaynshtejnは美しい性質を初めに証明し、いくつかの雑誌やウェブサイトで掲載された[2]:pp. 72–73。それは、 凸四角形が対角線の交点で4つの三角形に分割されていて、それら三角形の内心が共円ならば、その四角形は円に外接する、というものである。このとき4つの内心から成る四角形は円に内接する直角四角形である[2]:p.74。対角線の交点の角内にある傍接円に関しても、同様の性質が成り立ち、4つの傍心の成す四角形は円に内接する四角形となる[2]:p. 73。

凸四角形ABCDとその対角線の交点Pについて、角B,D内の△APB, △BPC, △CPD, △DPAの傍心が共円であることと、四角形が円に外接することは同値である[2]:p. 79。それらの傍接円半径をそれぞれR_a,R_b,R_c,R_dとして、以下の式が成り立つこともまた、四角形が円に外接する必要十分条件となる[2]:p. 80。

${\displaystyle {\frac {1}{R_{a}}}+{\frac {1}{R_{c}}}={\frac {1}{R_{b}}}+{\frac {1}{R_{d}}}.}$

さらに次の式が成り立つこともそれらと同値である[8]。

${\displaystyle {\frac {a}{\triangle (APB)}}+{\frac {c}{\triangle (CPD)}}={\frac {b}{\triangle (BPC)}}+{\frac {d}{\triangle (DPA)}}}$

ただし△(APB)でその三角形の面積を表す。

AP = p₁,BP = p₂,CP = q₁,DP = q₂とする。以下の式の成立も、四角形が円に外接する必要十分条件である[37]。

${\displaystyle ap_{2}q_{2}+cp_{1}q_{1}=bp_{1}q_{2}+dp_{2}q_{1}}$

または[2]:p. 74

${\displaystyle {\frac {(p_{1}+q_{1}-a)(p_{2}+q_{2}-c)}{(p_{1}+q_{1}+a)(p_{2}+q_{2}+c)}}={\frac {(p_{2}+q_{1}-b)(p_{1}+q_{2}-d)}{(p_{2}+q_{1}+b)(p_{1}+q_{2}+d)}}}$

または[2]:p. 77

${\displaystyle {\frac {(a+p_{1}-q_{1})(c+p_{2}-q_{2})}{(a-p_{1}+q_{1})(c-p_{2}+q_{2})}}={\frac {(b+p_{2}-q_{1})(d+p_{1}-q_{2})}{(b-p_{2}+q_{1})(d-p_{1}+q_{2})}}.}$

円に外接する四角形が、他の種類の四角形である条件

ひし形

円に外接する四角形の対角が等しいことと、その四角形がひし形であることは同値[38]。

凧形

円に外接する四角形が凧形であることは以下の様な条件がある[22]。

• 対角線によって面積が二等分される。
• 対角線が直交する。
• それぞれの対辺の内接円との接点を結んだ線分の長さが等しい。
• 接線長が、反対の接線長と等しい。
• 2組の対辺の中点を結んだ線分（bimedians）の長さが等しい。
• 2組の対辺の長さの積が等しい。
• 内接円の中心が対称の軸となる対角線上にある。

双心四角形

双心四角形ABCD。その接触四角形（桃）は直角四角形となる。

AB,BC,CD,DAと内接円の接点をそれぞれW,X,Y,Zとする。円に外接する四角形が外接円を持つ、つまり双心四角形であるための十分条件には以下の様なものがある[5][6]:p.124[27]。

• WY,XZが直交する。
• ${\displaystyle AW\cdot CY=BW\cdot DY}$
• ${\displaystyle {\frac {AC}{BD}}={\frac {AW+CY}{BX+DZ}}}$

一つ目の条件は接触四角形が直交対角線四角形となることである。

また、同じ辺長をもつどの円に外接する四角形よりも大きい内半径をもつ円に外接する四角形は双心四角形となる[39]:pp.392–393。

台形

円に外接する四角形がAB,CDが平行である円に外接する台形となるのは以下の式が成り立つときである[40]:Thm. 2。

${\displaystyle AW\cdot DY=BW\cdot CY}$

AD,BCが平行である場合は以下の式と同値である。

${\displaystyle AW\cdot BW=CY\cdot DY.}$

関連項目

• 外接する円（英語版）
• 傍接四角形
• 接線三角形
• 円外接多角形

出典

1. “円に外接する四角形とその性質”. 高校数学の美しい物語 (2022年1月15日). 2024年7月13日閲覧。
2. ^ Josefsson, Martin (2011), “More Characterizations of Tangential Quadrilaterals”, Forum Geometricorum 11: 65–82, http://forumgeom.fau.edu/FG2011volume11/FG201108.pdf .
3. 『幾何解法ノ極意』青野文魁堂、1901年、50頁。doi:10.11501/828418。https://dl.ndl.go.jp/pid/828418/1/50。 
4. 『幾何学問題集』有朋堂書店、1922年、259頁。doi:10.11501/949111。https://dl.ndl.go.jp/pid/949111/1/79。 
5. ^ Bryant, Victor; Duncan, John (2010), “Wheels within wheels”, The Mathematical Gazette 94 (November): 502–505 .
6. ^ JosefssonMartin「Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral」『Forum Geometricorum』第10巻、119–130頁、2010年。http://forumgeom.fau.edu/FG2010volume10/FG201013.pdf。 .
7. ^ Andreescu, Titu; Enescu, Bogdan (2006), Mathematical Olympiad Treasures, Birkhäuser, pp. 64–68 .
8. ^ MinculeteNicusor「Characterizations of a Tangential Quadrilateral」『Forum Geometricorum』第9巻、113–118頁、2009年。http://forumgeom.fau.edu/FG2009volume9/FG200910.pdf。 .
9. Josefsson, Martin (2012), “Similar Metric Characterizations of Tangential and Extangential Quadrilaterals”, Forum Geometricorum 12: 63–77, http://forumgeom.fau.edu/FG2012volume12/FG201207.pdf 
10. 長井, 熊吉、仲野, 雄介『測量設計實用表』（改訂）仲野雄介、1940年、431頁。doi:10.11501/845933。https://dl.ndl.go.jp/pid/845933/1/229。 
11. ^ Durell, C.V.; Robson, A. (2003), Advanced Trigonometry, Dover reprint, pp. 28–30 .
12. ^ Hajja, Mowaffaq (2008), “A condition for a circumscriptible quadrilateral to be cyclic”, Forum Geometricorum 8: 103–106, http://forumgeom.fau.edu/FG2008volume8/FG200814.pdf .
13. Durell, C.V.; Robson, A. (2003), Advanced Trigonometry, Dover reprint, pp. 28–30 .
14. Siddons, A.W.; Hughes, R.T. (1929), Trigonometry, Cambridge Univ. Press, p. 203 .
15. ^ Grinberg, Darij, Circumscribed quadrilaterals revisited, 2008
16. ^ Yiu, Paul, Euclidean Geometry, , 1998, pp. 156–157.
17. Hoyt, John P. (1986), “Maximizing the Area of a Trapezium”, American Mathematical Monthly 93 (1): 54–56, doi:10.2307/2322549 .
18. “Art of Problem Solving”. artofproblemsolving.com. 2024年7月13日閲覧。
19. Hoyt, John P. (1984), “Quickies, Q694”, Mathematics Magazine 57 (4): 239, 242 .
20. Josefsson, Martin (2010), “On the inradius of a tangential quadrilateral”, Forum Geometricorum 10: 27–34, http://forumgeom.fau.edu/FG2010volume10/FG201005.pdf .
21. “An Inradii Relation in Inscriptible Quadrilateral”. www.cut-the-knot.org. 2024年7月13日閲覧。
22. ^ Josefsson, Martin (2011), “When is a Tangential Quadrilateral a Kite?”, Forum Geometricorum 11: 165–174, http://forumgeom.fau.edu/FG2011volume11/FG201117.pdf .
23. Josefsson, Martin (2011), “The Area of a Bicentric Quadrilateral”, Forum Geometricorum 11: 155–164, http://forumgeom.fau.edu/FG2011volume11/FG201116.pdf .
24. “Geometry classes, Problem 152. Circumscribed Quadrilateral, Diagonal, Chord, Proportion. iPad Apps. Math teacher Master Degree. College, SAT Prep. Elearning, Online math tutor, LMS.”. gogeometry.com. 2024年7月13日閲覧。
25. “ニュートンの定理とその証明”. 高校数学の美しい物語 (2021年3月7日). 2024年7月13日閲覧。
26. Chakerian, G. D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979.
27. ^ Josefsson, Martin (2010), “Characterizations of Bicentric Quadrilaterals”, Forum Geometricorum 10: 165–173, http://forumgeom.fau.edu/FG2010volume10/FG201019.pdf .
28. Myakishev, Alexei (2006), “On Two Remarkable Lines Related to a Quadrilateral”, Forum Geometricorum 6: 289–295, http://forumgeom.fau.edu/FG2006volume6/FG200634.pdf .
29. Dergiades, Nikolaos; Christodoulou, Dimitris M. (2017), “The two incenters of an arbitrary convex quadrilateral”, Forum Geometricorum 17: 245–254, http://forumgeom.fau.edu/FG2017volume17/FG201727.pdf .
30. Andreescu, Titu; Feng, Zuming (2005), 103 Trigonometry Problems From the Training of the USA IMO Team, Birkhäuser, pp. 176–177 .
31. “Art of Problem Solving (2011)”. artofproblemsolving.com. 2024年7月13日閲覧。
32. Barton, Helen (1926), “On a circle attached to a collapsible four-bar”, American Mathematical Monthly 33 (9): 462–465, doi:10.2307/2299611, JSTOR 2299611, https://jstor.org/stable/2299611 .
33. “When A Quadrilateral Is Inscriptible?”. www.cut-the-knot.org. 2024年7月13日閲覧。
34. Chao, Wu Wei; Simeonov, Plamen (2000), “When quadrilaterals have inscribed circles (solution to problem 10698)”, American Mathematical Monthly 107 (7): 657–658, doi:10.2307/2589133 .
35. ^ Vaynshtejn, I.; Vasilyev, N.; Senderov, V. (1995), “(Solution to problem) M1495”, Kvant (6): 27–28. 
36. Josefsson, Martin (2012), “Characterizations of Orthodiagonal Quadrilaterals”, Forum Geometricorum 12: 13–25, http://forumgeom.fau.edu/FG2012volume12/FG201202.pdf .
37. Hoehn, Larry (2011), “A new formula concerning the diagonals and sides of a quadrilateral”, Forum Geometricorum 11: 211–212, http://forumgeom.fau.edu/FG2011volume11/FG201122.pdf .
38. De Villiers, Michael (2011), “Equiangular cyclic and equilateral circumscribed polygons”, Mathematical Gazette 95 (March): 102–107 .
39. Hess, Albrecht (2014), “On a circle containing the incenters of tangential quadrilaterals”, Forum Geometricorum 14: 389–396, http://forumgeom.fau.edu/FG2014volume14/FG201437.pdf .
40. Josefsson, Martin (2014), “The diagonal point triangle revisited”, Forum Geometricorum 14: 381–385, http://forumgeom.fau.edu/FG2014volume14/FG201435.pdf .

外部リンク

• Weisstein, Eric W. "Tangential Quadrilateral". mathworld.wolfram.com (英語).