内接多角形 P の外接円 C および外心 O 初等幾何学 における多角形 の外接円 (がいせつえん、英 : circumscribed circle , circumcircle 頂点 を通る円 をいう。外接円の中心 を外心 (circumcenter ) といい、その半径を外接半径 (circumradius ) という。
外接円を持つ多角形は、円内接多角形 (inscribed polygon ), cyclic polygon (輪状多角形) あるいは、そのすべての頂点が同一円周上にある(つまり、共円 である)ことにより共円多角形 (concyclic polygon )などと呼ばれる。任意の正 単純多角形 や任意の等脚台形 、任意の三角形 、任意の長方形 は共円多角形の例となる。
よく似た概念の一つに最小包含円 (英語版 ) minimum bounding circle ) があり、これはその多角形を完全に含む最小の円をいう。(多角形のすべての頂点が同一円周上にある必要はないことより)必ずしも任意の多角形に外接円が存在するとは限らないが、任意の多角形は最小包含円をただ一つ持つ(それを線形時間 で構成するアルゴリズムがある)。多角形が外接円を持つ場合であっても、外接円と最小包含円が一致するとは限らない。例えば鈍角三角形 の最小包含円は最長辺を直径とする円で、これは最長辺の対角の頂点を通らない。
三角形において、ある頂点と、その対辺の垂直二等分線 の延長線上にある外接円(円周)との交点(対辺からみて三角形の外側の方)を結ぶ直線は、 その頂点の内角を二等分する直線となっている。(図中に緑の直線で示される。それらの交点は当該三角形の内接円 の中心となっている。) すべての三角形には外接円が存在する。三角形の外心は、3つの辺 の垂直二等分線 が交わる点である。
航海において、三角形の外接円は方位磁針 が使用できない状況で六分儀 を利用して位置を割り出すのに使用されることがある。
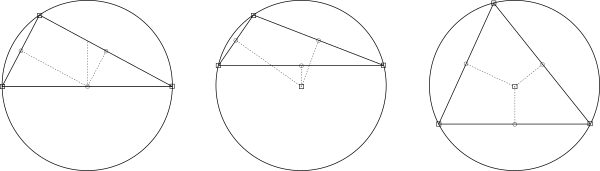
鋭角三角形 の外心は三角形の内部にあり、鈍角三角形 の外心は三角形の外部にある。直角三角形 の外心は斜辺 の中点 である。
外接円の直径 は、辺の長さとその辺に対する頂点の角度から求めることができる。これを正弦定理 という。
三角形の外心はその三角形の重心 ・垂心 と同じ直線上にある。この直線をオイラー線 という。三角形の九点円 の半径は、外接円の半径の半分である。
直交座標系 における外接円の式は行列式 を用いて以下のように表すことができる。
det
|
v
2
v
x
v
y
1
A
2
A
x
A
y
1
B
2
B
x
B
y
1
C
2
C
x
C
y
1
|
=
0
{\displaystyle \det {\begin{vmatrix}v^{2}&v_{x}&v_{y}&1\\A^{2}&A_{x}&A_{y}&1\\B^{2}&B_{x}&B_{y}&1\\C^{2}&C_{x}&C_{y}&1\end{vmatrix}}=0}
ここで、A , B , C は各頂点を表す。この式を満たす v の集合が外接円となる(A 2 = A x 2 + A y 2 とする)。
外心を三線座標 で表すと、
(
cos
(
α
)
,
cos
(
β
)
,
cos
(
γ
)
)
{\displaystyle \left(\cos(\alpha ),\cos(\beta ),\cos(\gamma )\right)}
[ 2] :19 。ここで、α,β,γ は3つの角の大きさとする。重心座標 で表すと、
(
sin
(
2
α
)
,
sin
(
2
β
)
,
sin
(
2
γ
)
)
{\displaystyle \left(\sin(2\alpha ),\sin(2\beta ),\sin(2\gamma )\right)}
(
a
2
(
−
a
2
+
b
2
+
c
2
)
,
b
2
(
a
2
−
b
2
+
c
2
)
,
c
2
(
a
2
+
b
2
−
c
2
)
)
{\displaystyle \left(a^{2}(-a^{2}+b^{2}+c^{2}),\;b^{2}(a^{2}-b^{2}+c^{2}),\;c^{2}(a^{2}+b^{2}-c^{2})\right)}
[ 3]
a
,
b
,
c
{\displaystyle a,b,c}
各頂点の位置ベクトルを
A
,
B
,
C
{\displaystyle A,B,C}
a
,
b
,
c
{\displaystyle a,b,c}
U
{\displaystyle U}
U
=
a
2
(
b
2
+
c
2
−
a
2
)
A
+
b
2
(
c
2
+
a
2
−
b
2
)
B
+
c
2
(
a
2
+
b
2
−
c
2
)
C
a
2
(
b
2
+
c
2
−
a
2
)
+
b
2
(
c
2
+
a
2
−
b
2
)
+
c
2
(
a
2
+
b
2
−
c
2
)
.
{\displaystyle U={\frac {a^{2}(b^{2}+c^{2}-a^{2})A+b^{2}(c^{2}+a^{2}-b^{2})B+c^{2}(a^{2}+b^{2}-c^{2})C}{a^{2}(b^{2}+c^{2}-a^{2})+b^{2}(c^{2}+a^{2}-b^{2})+c^{2}(a^{2}+b^{2}-c^{2})}}.}
この式の分母は、三角形の面積を
S
{\displaystyle S}
16
S
2
{\displaystyle 16S^{2}}
外接円の半径は以下のような式で表される。
R
=
a
b
c
4
s
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
=
a
b
c
4
r
s
=
r
cos
A
+
cos
B
+
cos
C
−
1
{\displaystyle {\begin{aligned}R&={\frac {abc}{4{\sqrt {s(s-a)(s-b)(s-c)}}}}\\&={\frac {abc}{4rs}}\\&={\frac {r}{\cos A+\cos B+\cos C-1}}\end{aligned}}}
ここで、a,b,c は3辺の長さ、A,B,C は3つの角の大きさ、r は内接円 の半径、s は半周長 を意味する。
円に内接する四角形 外接円を持つ四辺形 四角形が特定の条件—例えば対角が補角 (互いに加えて180° あるいはπ ラジアン)となること—を満たすとき、円を外接させることができる。
これを満たす代表的な四角形として、長方形 ・等脚台形 があげられる。
外接円の半径は
R
=
1
4
(
a
c
+
b
d
)
(
a
d
+
b
c
)
(
a
b
+
c
d
)
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
{\displaystyle R={\frac {1}{4}}{\sqrt {\frac {(ac+bd)(ad+bc)(ab+cd)}{(s-a)(s-b)(s-c)(s-d)}}}}
で表すことができる(ブラーマグプタの公式 )。s は半周長 である。
4つの辺の長さを a, b, c, d 、対角線の長さを p, q とすると、ac + bd = pq が成り立つ(トレミーの定理 )。
外接円と内接円 の両方が存在する四角形を双心四角形 という。
共円奇数角形の全ての角の角度が等しくなるための必要十分条件は、それが正多角形となることである。共円偶数角形の全ての角の角度が等しくなるための必要十分条件は、辺の長さが交互に等しい(つまり、各辺に対しそれに隣接する二つの辺同士の長さが互いに等しい[ 注釈 1] [ 4]
辺の長さと面積がすべて有理数 となるような共円五角形 はロビンスの五角形 (英語版 ) [ 5]
偶数 n に対する任意の共円 n -角形について、その角を交互に二つの組に分けるとき、それぞれの組に属する角の和をとればそれらは互いに等しい(「奇数番目の角の和」=「偶数番目の角の和」)。このことは n = 4n -角形の交互の角の和にそれぞれ加えられるが、それら和が互いに等しいことは変わらない)。
一つの n -角形 X が円 C に内接し、別の n 角形 Y が先の n -角形 X の各頂点で接する ように円 C に外接 しているものとする。このとき円 C 上の任意の点 P から多角形 X の各辺に引いた垂線の長さの総乗は P から多角形 Y の各辺に引いた垂線の長さの総乗に等しい[ 6] :p. 72 。
^ どこかの辺を1番目として時計回りに順に番号を振るならば、1, 3, 5, … 番目が互いに等しい一組で、2, 4, 6, … 番目が互いに等しいもう一組
^ Whitworth, William Allen. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions , Forgotten Books, 2012 (orig. Deighton, Bell, and Co., 1866). http://www.forgottenbooks.com/search?q=Trilinear+coordinates&t=books
^ Weisstein, Eric W. "barycentric coordinates" . mathworld.wolfram.com (英語). ^ De Villiers, Michael. "Equiangular cyclic and equilateral circumscribed polygons," Mathematical Gazette
^
Buchholz, Ralph H.; MacDougall, James A. (2008), “Cyclic polygons with rational sides and area” , Journal of Number Theory 128 (1): 17–48, doi :10.1016/j.jnt.2007.05.005 , MR 2382768 , http://docserver.carma.newcastle.edu.au/785/
^ Johnson, Roger A., Advanced Euclidean Geometry , Dover, 2007 (orig. 1929).
Megiddo, N. (1983). “Linear-time algorithms for linear programming in R 3 and related problems”. SIAM Journal on Computing 12 (4): 759–776. doi :10.1137/0212052 .