ハイパーグラフ

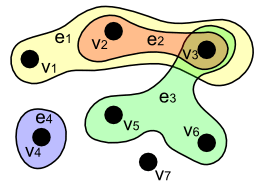
ハイパーグラフの例: ${\displaystyle X=\{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6},v_{7}\}}$, ${\displaystyle E=\{e_{1},e_{2},e_{3},e_{4}\}}$ ${\displaystyle =\{\{v_{1},v_{2},v_{3}\},\{v_{2},v_{3}\},}$ ${\displaystyle \{v_{3},v_{5},v_{6}\},\{v_{4}\}\}}$.

ハイパーグラフ（英: Hypergraph）とは、数学におけるグラフを一般化（拡張）したもので、エッジ（枝）が任意個数のノード（頂点）を連結できる。形式的には ${\displaystyle (X,E)}$ という対で表され、${\displaystyle X}$ はノードあるいは頂点と呼ばれる要素の集合、${\displaystyle E}$ はハイパーエッジ（hyperedge）と呼ばれる ${\displaystyle X}$ の空集合でない部分集合の集合である。したがって、${\displaystyle E}$ は ${\displaystyle {\mathcal {P}}(X)\setminus \{\emptyset \}}$ の部分集合である。ただし、${\displaystyle {\mathcal {P}}(X)}$ は ${\displaystyle X}$ の冪集合を表す。通常のグラフのエッジは2つのノードの対で表されるが、ハイパーエッジは任意のノードの集合で表され、任意個のノードを含む。

グラフとは異なり、ハイパーグラフは紙上に図示するのが困難である。そのため、グラフ理論のような図解をされることは少なく、集合論の用語で表される傾向がある。

概要

グラフ理論の多くの定理はハイパーグラフでも成り立つ。典型例としてラムゼーの定理がある。グラフの対称性に関する研究もハイパーグラフに拡張して適用可能である。ハイパーグラフが準同型であるとは、あるハイパーグラフの頂点集合から別のそれへの写像があり、1つのエッジがもう一方のエッジに対応することを意味する。ハイパーグラフが同型であるとは、逆向きにも準同型である場合をいう。ハイパーグラフが自己同型であるとは、頂点集合がラベルを付け直した頂点集合と準同型であることをいう。ハイパーグラフの自己同型の集合 H (= (X, E)) は、合成について群となり、ハイパーグラフの自己同型群と呼ばれ Aut(H) で表される。ハイパーグラフの集まりは、射としてのハイパーグラフ準同型の集まりからなる圏である。

ハイパーグラフ H = (X, E) の「横断（transversal）」または「ヒッティングセット（hitting set）」${\displaystyle T\subseteq X}$ とは、どのエッジとも、積集合が空ではない集合のことである。すなわち、Tと各エッジの間に共通なノードが必ず存在する。横断 T は、その真部分集合として横断と呼べるものがない場合に「最小」であるという。H の「横断ハイパーグラフ」は (X, F) で表されるハイパーグラフであり、F は H の全最小横断からなる。横断ハイパーグラフの計算は、機械学習などの計算機科学分野で応用されており、ゲーム理論、データベースのインデックス付け、充足可能性問題、最適化などと関連する。

各エッジの濃度（元の個数）が k であるようなハイパーグラフを「k一様（k-uniform）」または「kハイパーグラフ（k-hypergraph）」と呼ぶ。グラフは2一様なハイパーグラフである。頂点 v の次数 d(v) とは、その頂点が属するエッジの個数である。全ての頂点の次数が k であるハイパーグラフを「k正則（k-regular）」であるという。

ここで、${\displaystyle V=\{v_{1},v_{2},~\ldots ,~v_{n}\}}$ と ${\displaystyle E=\{e_{1},e_{2},~\ldots ,~e_{m}\}}$ があるとする。全てのハイパーグラフには ${\displaystyle n\times m}$ の「接続行列」${\displaystyle A=(a_{ij})}$ があり、以下が成り立つ。

${\displaystyle a_{ij}=\left\{{\begin{matrix}1&\mathrm {if} ~v_{i}\in e_{j}\\0&\mathrm {otherwise} \end{matrix}}\right.}$

接続行列の転置行列 ${\displaystyle A^{t}}$ により定義されるハイパーグラフ ${\displaystyle H^{*}=(V^{*},E^{*})}$ を ${\displaystyle H}$ の「双対（dual）」であるといい、${\displaystyle V^{*}}$ は m 個の元からなる集合、${\displaystyle E^{*}}$ は n 個の ${\displaystyle V^{*}}$ の部分集合からなる集合である。${\displaystyle v_{j}^{*}\in V^{*}}$ と ${\displaystyle e_{i}^{*}\in E^{*}}$ について ${\displaystyle a_{ij}=1}$ であるときのみ ${\displaystyle ~v_{j}^{*}\in e_{i}^{*}}$ である。一様なハイパーグラフの双対は、正則であり、逆も成り立つ。双対を考えることで新たな発見があることが多い。

ハイパーグラフの彩色

ハイパーグラフの彩色は次のように定義される。${\displaystyle H=(V,E)}$ というハイパーグラフは ${\displaystyle \Vert V\Vert =n}$ であるとする。${\displaystyle C=\{c_{1},c_{2},\ldots ,c_{n}\}}$ が ${\displaystyle H}$ の妥当な彩色であるとは、全ての ${\displaystyle e\in E,\vert e\vert >1}$ について任意の頂点 ${\displaystyle v_{i},v_{j}\in e}$ で ${\displaystyle c_{i}\neq c_{j}}$ となる場合のみを指す。

関連項目

• 素集合
• 集合の分割
• 有限交叉性
• 頂点被覆

この記事は、クリエイティブ・コモンズ・ライセンス 表示-継承 3.0 非移植のもと提供されているオンライン数学辞典『PlanetMath』の項目hypergraphの本文を含む