|
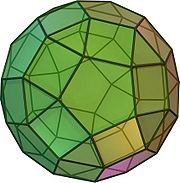
Rombicosidodecaedro
In geometria solida il rombicosidodecaedro (o piccolo rombicosidodecaedro) è uno dei tredici poliedri archimedei. Ha 62 facce, di cui 12 pentagonali, 30 quadrate e 20 triangolari, 120 spigoli e 60 vertici, in ciascuno dei quali concorrono un pentagono, due quadrati e un triangolo. Area e volumeL'area A ed il volume V di un rombicosidodecaedro i cui spigoli hanno lunghezza a sono le seguenti: DualitàIl poliedro duale del rombicosidodecaedro è l'esacontaedro deltoidale (o esacontaedro trapezoidale). SimmetrieIl gruppo delle simmetrie del rombicosidodecaedro ha 120 elementi; il gruppo delle simmetrie che preservano l'orientamento è il gruppo icosaedrale . Sono gli stessi gruppi di simmetria dell'icosaedro, del dodecaedro e dell'icosidodecaedro.
Altri solidiIl rombicosidodecaedro può essere ottenuto sia dall'icosaedro che dal dodecaedro tramite espansione, ovvero allontanando dal centro le facce del solido e creando nuove facce per ogni spigolo o vertice di partenza.. Il rombicosidodecaedro può essere ottenuto anche troncando al contempo tanto le cuspidi quanto gli spigoli dell'icosaedro o, equivalentemente, del dodecaedro. Le venti facce triangolari e le dodici facce pentagonali del rombicosidodecaedro giacciono sui piani delle facce di un icosaedro e di un dodecaedro, rispettivamente. Le trenta facce quadrate, invece, giacciono sugli stessi piani delle facce di un triacontaedro rombico, poliedro duale dell'icosidodecaedro. La troncatura delle trenta cuspidi dell'icosidodecaedro origina un poliedro simile al rombicosidodecaedro, ma con facce non regolari.  Solidi di JohnsonAl rombicosidodecaedro sono correlati alcuni solidi di Johnson, poliedri aventi poligoni regolari per facce. Tagliando una cupola pentagonale, ad esempio, si ottiene un rombicosidodecaedro diminuito; la cupola può venire nuovamente incollata, ma se si allineano quadrati con quadrati e triangoli con pentagoni si ottiene un solido diverso da quello di partenza: il rombicosidodecaedro girato. La stessa operazione può essere effettuata su più cupole, a patto che esse non abbiano elementi comuni. Agendo su due cupole si possono ottenere due tipi di rombicosidodecaedro bigirato: il rombicosidodecaedro parabigirato qualora le due cupole siano opposte e il romicosidodecaedro metabigirato altrimenti. Ruotando tre cupole si ottiene invece il rombicosidodecaedro trigirato.
Bibliografia
Voci correlateAltri progetti
Collegamenti esterni
|
|||||||||||||||||||||||||||||||||||||||||||||||||