ro Bipiramid%C4%83 octogonal%C4%83

Descriere
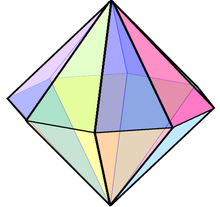
Bipiramidă octogonală

Tip	bipiramidă
Fețe	16 triunghiuri isoscele
Laturi (muchii)	24
Vârfuri	10
χ	2
Configurația feței	V4.4.8
Simbol Schläfli	{ } + {8}
Diagramă Coxeter
Grup de simetrie	D_8h, [8,2], (*228), ordin 32
Grup de rotație	D₈, [8,2]⁺, (228), ordin 16
Poliedru dual	prismă octogonală
Proprietăți	convexă, tranzitivă pe fețe^[1]

În geometrie o bipiramidă octogonală este un poliedru format prin unirea a două piramide octogonale prin bazele lor.^[2]^[3] O bipiramidă octogonală are 16 fețe triunghiulare, 24 de laturi (muchii) și 10 vârfuri.

Deși este tranzitivă pe fețe,^[1] nu este un poliedru platonic deoarece în unele vârfuri se întâlnesc câte patru fețe, iar în altele câte opt. Nu este nici poliedru Johnson deoarece fețele sale nu pot fi triunghiuri echilaterale; într-un spațiu tridimensional 8 triunghiuri echilaterale pot avea un vârf comun doar într-un spațiu hiperbolic.

Este una dintr-o mulțime infinită de bipiramide. Având 16 fețe, este un hexadecaedru.

Bipiramida octogonală are un plan de simetrie (orizontal în figura din dreapta) unde bazele celor două piramide sunt unite. Secțiunea în acest plan este un octogon. De asemenea, există opt plane de simetrie care trec prin cele două apexuri, situate la unghiuri de 22,5° unul față de celălalt și sunt perpendiculare pe planul orizontal. Secțiunile din aceste plane sunt romburi.

Formule pentru bipiramida regulată dreaptă

Pentru o bipiramidă octogonală regulată cu latura $a$ și semiînălțimea $h$ (jumătate din distanța dintre apexuri) aria $A$ este dată de formula:^[4]^[5]

A=8a{\sqrt {{\frac {3+2{\sqrt {2}}}{4}}a^{2}+h^{2}}}

Pentru $a$ = 1 și $h$ = 1 aria este ≈ 12,5401289.

Formula volumului $V$ este:^[4]^[5]

V={\frac {4}{3}}({\sqrt {2}}+1)\,a^{2}h

Pentru $a$ = 1 și $h$ = 1 volumul este ≈ 3,2189514.

Pavare sferică

Poate fi văzută ca o pavare a unei sfere, fețele reprezentând și domeniile fundamentale ale simetriei diedrale [4,2], *422.

Poliedre înrudite

Bipiramide n-gonale (simetrice) drepte „regulate”:
Numele bipiramidei	Bipiramidă digonală	Bipiramidă triunghiulară (v. J₁₂)	Bipiramidă tetragonală (v. O)	Bipiramidă pentagonală (v. J₁₃)	Bipiramidă hexagonală	Bipiramidă heptagonală	Bipiramidă octogonală	Bipiramidă eneagonală	Bipiramidă decagonală	...	Bipiramidă apeirogonală
Imagine										...
Pavare sferică										Pavare plană
Config. feței	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Diagramă Coxeter										...

Variante de pavări omnitrunchiate cu simetrie n42: 4.8.2n*
Simetrie *n42 [n,3]	Sferice		Euclidiană	Hiperbolice compacte				Paracomp.
Simetrie *n42 [n,3]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Figuri omnitrunchiate	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Duale omnitrunchiate	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞