|
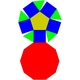
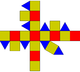
Poliedru JohnsonGirobicupola pătrată alungită, (J37), este un poliedru Johnson Octaedrul stelat nu este un poliedru Johnson deoarece nu este convex Acest poliedru cu 24 de fețe pătrate nu este un poliedru Johnson deoarece nu este strict convex (are unghiuri diedre de 180°) În geometrie, un poliedru Johnson este un poliedru strict convex ale cărui fețe sunt poligoane regulate. Nu există condiția ca toate fețele să fie același poligon sau că aceleași poligoane să se întâlnească în jurul fiecărui vârf. Un exemplu de poliedru Johnson este piramida pătrată echilaterală, J1, care are o față pătrată și 4 fețe triunghiulare. Unii autori cer ca poliedrul să nu fie uniform, adică să nu fie poliedru platonic, poliedru arhimedic, prismă uniformă sau antiprismă uniformă, pe care nu le consideră „poliedre Johnson”. Ca la orice poliedru strict convex, cel puțin trei fețe se întâlnesc în fiecare vârf, iar suma unghiurilor lor din dreptul unui vârf este mai mică de 360°. Deoarece un poligon regulat are unghiuri de cel puțin 60 de grade, rezultă că cel mult cinci fețe se întâlnesc în orice vârf. Piramida pentagonală (J2) este un exemplu care are un vârf de gradul 5. Deși nu există nicio restricție evidentă că un anumit poligon regulat nu ar putea fi o față a unui poliedru Johnson, se pare că fețele poliedrelor Johnson care nu sunt uniforme (adică nu sunt un poliedru platonic, arhimedic, prismă sau antiprismă uniforme) au întotdeauna 3, 4, 5, 6, 8 sau 10 laturi. În 1966, Norman Johnson a publicat o listă care include toate cele 92 de poliedre Johnson (excluzând cele 5 poliedre platonice, cele 13 poliedre arhimedice și infinit de multele prisme și antiprisme uniforme) și le-a dat numele și numerele lor. El nu a demonstrat că există doar 92, dar a conjecturat că nu există altele. În 1967 Victor Zalgaller a demonstrat că lista lui Johnson era completă.[1] Dintre poliedrele Johnson, girobicupola pătrată alungită (J 37 ), numită și pseudorombicuboctaedru,[2] este unică prin faptul că este uniformă local la nivel de vârf: în fiecare vârf se întâlnesc 4 fețe, iar dispunerea lor este întotdeauna aceeași: 3 pătrate și 1 triunghi. Totuși, ea nu este tranzitivă pe vârfuri, deoarece are izometrie diferită în vârfuri diferite, făcându-l mai degrabă un poliedru Johnson decât un poliedru arhimedic. DenumiriDenumirile poliedrelor Johnson se formează pe baza unei formule descriptive flexibile și precise, astfel încât multe poliedre pot fi denumite în moduri diferite fără a compromite acuratețea lor ca descriere. Majoritatea poliedrelor Johnson pot fi construite din primele câteva piramide, cupole și rotonde, împreună cu poliedrele platonice și arhimedice, prisme și antiprisme. În limba română începutul numelui unui anumit poliedru va conține aceste noțiuni. De acolo, o serie de prefixe și sufixe sunt atașate cuvântului pentru a indica adăugiri, rotații și transformări:
Ultimele trei operații — augmentare, diminuare și girare — pot fi efectuate de mai multe ori la anumite poliedre mari. Bi- și Tri- indică o operație dublă, respectiv triplă. De exemplu, un poliedru bigirat are două cupole rotite, iar un poliedru tridiminuat are trei piramide sau cupole îndepărtate. La anumite poliedre mari se face distincția între poliedrele la care fețele modificate sunt paralele și poliedrele în care fețele modificate sunt oblice. Para- indică primul caz, că poliedrul respectiv are fețele paralele modificate, iar Meta- indică al doilea caz, că poliedrul respectiv are fețele oblice modificate. De exemplu, un poliedru parabiaugmentat a avut două fețe paralele augmentate, iar un poliedru metabigirat a avut două fețe oblice rotite. Ultimele câteva poliedre Johnson au nume bazate pe anumite complexe poligonale din care sunt asamblate. Aceste nume sunt definite de Johnson[3] în modul următor:
EnumerarePiramide, cupole și rotondePrimele 6 poliedre Johnson sunt piramide, cupole sau rotonde cu cel mult 5 fețe laterale. Piramidele și cupolele cu 6 sau mai multe fețe laterale sunt coplanare și, prin urmare, nu sunt poliedre Johnson. PiramidePrimele două poliedre Johnson, J1 și J2, sunt piramide. Piramida triunghiulară este tetraedrul regulat, deci nu este un poliedru Johnson. J1 și J2 reprezintă părți ale poliedrelor regulate.
Cupole și rotondeUrmătoarele patru poliedre Johnson sunt trei cupole și o rotondă. Ele sunt părți ale poliedrelor uniforme.
Piramide modificatePoliedrele Johnson 7–17 sunt derivate din piramide. Piramide alungite și giroalungiteÎn piramida triunghiulară giroalungită, trei perechi de triunghiuri adiacente sunt coplanare și formează câte un romb nepătrat, deci nu este un poliedru Johnson.
BipiramideBipiramida pătrată este octaedrul regulat, în timp ce bipiramida pentagonală giroalungită este icosaedrul regulat, deci nu sunt solide Johnson. În bipiramida triunghiulară giroalungită șase perechi de triunghiuri adiacente sunt coplanare și formează romburi nepătrate, deci, de asemenea, nu este un solid Johnson.
Cupole și rotonde modificatePoliedrele Johnson 18–48 derivă din cupole și rotonde. Cupole și rotonde alungite și giroalungite
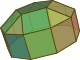
BicupoleGirobicupola triunghiulară este un poliedru arhimedic (în acest caz cuboctaedrul), deci nu este un poliedru Johnson.
Cupole-rotonde și birotondeGirobirotonda pentagonală este un poliedru arhimedic (în acest caz icosidodecaedrul), deci nu este un poliedru Johnson.
Bicupole alungiteOrtobicupola pătrată alungită este un poliedru arhimedic (în acest caz rombicuboctaedrul), deci nu este un poliedru Johnson.
Cupole-rotonde și birotonde alungite
Bicupole giroalungite, cupole-rotonde și birotondeAceste poliedre Johnson au două forme chirale.
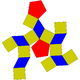
Prisme augmentatePoliedrele Johnson 49–57 sunt construite prin augmentarea fețelor laterale ale prismelor cu piramide pătrate.
Poliedre platonice modificatePoliedrele Johnson 58–64 sunt construite prin augmentarea sau diminuarea poliedrelor platonice. Dodecaedre augmentate
Icosaedre diminuate și diminuate–augmentate
Poliedre arhimedice modificatePoliedrele Johnson 65–83 sunt construite prin augmentarea, diminuarea sau girarea poliedrelor arhimedice. Poliedre arhimedice augmentate
Rombicosidodecaedre diminuate girate
J37 ar apărea și aici ca duplicat (este un rombicuboctaedru girat). Alte poliedre arhimedice diminuate și girateAlte poliedre arhimedice pot fi girate și diminuate, dar toate au ca rezultat poliedrele enumerate anterior.
Poliedre elementarePoliedrele Johnson 84–92 nu sunt derivate din manipulările „tăiat și lipit” ale poliedrelor uniforme. Antiprisme snubAntiprismele snub pot fi construite prin alternarea antiprismelor trunchiate. Girobianticupolele sunt o altă construcție pentru antiprismele snub. Doar antiprismele snub cu cel mult 4 fețe pot fi construite din poligoane regulate. Antiprisma triunghiulară snub este icosaedrul regulat, deci nu este un poliedru Johnson.
Altele
Clasificarea după tipul fețelorPoliedre Johnson cu fețe triunghiulareCinci poliedre Johnson sunt deltaedre, având toate fețele triunghiuri echilaterale: Poliedre Johnson cu fețe triunghiulare și pătrateDouăzeci și patru de poliedre Johnson au doar fețe triunghiulare și pătrate: Poliedre Johnson cu fețe triunghiulare și pentagonaleUnsprezece poliedre Johnson au doar fețe triunghiulare și pentagonale: Poliedre Johnson cu fețe triunghiulare, pătrate și pentagonaleDouăzeci de poliedre Johnson au doar fețe triunghiulare, pătrate și pentagonale: Poliedre Johnson cu fețe triunghiulare, pătrate și hexagonaleOpt poliedre Johnson au doar fețe triunghiulare, pătrate și hexagonale: Poliedre Johnson cu fețe triunghiulare, pătrate și octogonaleCinci poliedre Johnson au doar fețe triunghiulare, pătrate și octogonale: Poliedre Johnson cu fețe triunghiulare, pentagonale și decagonaleDouă poliedre Johnson au doar fețe triunghiulare, pătrate și decagonale: Poliedre Johnson cu fețe triunghiulare, pătrate, pentagonale și hexagonaleUn singur poliedru Johnson are fețe triunghiulare, pătrate pentagonale și hexagonale: Poliedre Johnson cu fețe triunghiulare, pătrate, pentagonale și decagonaleȘaisprezece poliedre Johnson au doar fețe triunghiulare, pătrate pentagonale și decagonale: Poliedre Johnson inscriptibile25 de poliedre Johnson au vârfurile pe suprafața unei sfere: 1–6,11,19,27,34,37,62,63,72–83. Toate acestea provin din câte un poliedru regulat sau uniform prin girare, diminuare sau disecție.[4]
Note
Bibliografie
Vezi șiLegături externe
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia