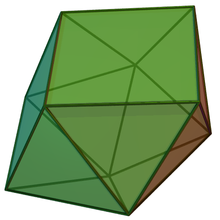
În geometrie sfenocoroana este unul dintre poliedrele Johnson (J 86 ). Este unul dintre poliedrele elementare Johnson care nu se pot obține prin „tăiere și lipire” ale poliedrelor platonice sau arhimedice . Având 14 fețe , este un tetradecaedru .
Johnson folosește prefixul sfeno- pentru a se referi la un complex asemănător unei pene format din două lunule pătrat cu triunghiuri echilaterale atașate pe laturile opuse). De asemenea, sufixul -coroană se referă la un complex în formă de coroană, format din 8 triunghiuri echilaterale. Unirea ambelor complexe produce sfenocoroana.[ 1]
Coordonate carteziene
Fie k ≈ 0,85273 cea mai mică rădăcină pozitivă a polinomului de gradul patru:
60
x
4
−
48
x
3
−
100
x
2
+
56
x
+
23.
{\displaystyle 60x^{4}-48x^{3}-100x^{2}+56x+23.}
Atunci, coordonatele carteziene ale unei sfenocoroane cu lungimea laturilor egală cu 2 sunt date de reuniunea orbitelor punctelor
(
0
,
1
,
2
1
−
k
2
)
,
(
2
k
,
1
,
0
)
,
(
0
,
1
+
3
−
4
k
2
1
−
k
2
,
1
−
2
k
2
1
−
k
2
)
,
(
1
,
0
,
−
2
+
4
k
−
4
k
2
)
{\displaystyle \left(0,1,2{\sqrt {1-k^{2}}}\right),\,(2k,1,0),\left(0,1+{\frac {\sqrt {3-4k^{2}}}{\sqrt {1-k^{2}}}},{\frac {1-2k^{2}}{\sqrt {1-k^{2}}}}\right),\,\left(1,0,-{\sqrt {2+4k-4k^{2}}}\right)}
sub acțiunea grupului de simetrie generat de reflexiile față de planele xz și yz .[ 2]
Aria suprafeței unei sfenocoroane cu laturile de lungime a se poate calcula cu relația:[ 3]
A
=
(
2
+
3
3
)
a
2
≈
7
,
196152
a
2
,
{\displaystyle A=\left(2+3{\sqrt {3}}\right)a^{2}\approx 7,196152\,a^{2},}
iar volumul cu:[ 4]
V
=
1
2
1
+
3
3
2
+
13
+
3
6
a
3
≈
1
,
515352
a
3
.
{\displaystyle V={\frac {1}{2}}{\sqrt {1+3{\sqrt {\frac {3}{2}}}+{\sqrt {13+3{\sqrt {6}}}}}}\,a^{3}\approx 1,515352\,a^{3}.}
Diverse
Ca figură a vârfului a marii antiprisme Sfenocoroana este figura vârfului antiprismoidelor duble n -gonaleizogonale , unde n este un număr impar mai mare ca 1, inclusiv marea antiprismă . De notat că aceste antiprismoide au mai degrabă fețe trapezoidale , nu pătrate.
Note
^ en Johnson, Norman W. (1966 ), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics , 18 : 169–200, doi :10.4153/cjm-1966-021-8 , MR 0185507 , Zbl 0132.14603 ^ en Timofeenko, A. V. (2009 ). „The non-Platonic and non-Archimedean noncomposite polyhedra”. Journal of Mathematical Science . 162 (5): 718. doi :10.1007/s10958-009-9655-0 . ^ en Wolfram Research, Inc. (2020 ). „Wolfram|Alpha Knowledgebase”. Champaign, IL. PolyhedronData[{"Johnson", 86}, "SurfaceArea"] ^ en Wolfram Research, Inc. (2020 ). „Wolfram|Alpha Knowledgebase”. Champaign, IL. PolyhedronData[{"Johnson", 86}, "Volume"]
Piramide, cupole și rotonde modificate
Piramide modificate Bipiramide Cupole modificate Bicupole șiRotonde modificate Cupolerotonde