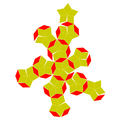
菱形九十面體是一種由90個菱形組成的凸多面體,屬於環帶多面體[2][3],是截半截角二十面體的對偶多面體,由90個面、180條邊和92個頂點所組成[1],並具有二十面體群對稱性。[4][1]
組成菱形九十面體的菱形有兩種,一種較寬、另一種較窄[5],其中,較寬的菱形有60個、較窄的菱形有30個,構成的方式有3個菱形的公共頂點、5個菱形的公共頂點和6個菱形的公共頂點。[1]
性質
菱形九十面體由90個面、180條邊和92個頂點所組成。[1]在其90個面中,有60個較寬的菱形和30個較窄的菱形[6]。在其92個頂點中,有60個頂點是3個菱形的公共頂點、12個頂點是5個菱形的公共頂點和20個頂點是6個菱形的公共頂點。[1]在對稱性上,菱形九十面體共有12個具有5倍對稱性的頂點,位於5個較寬之菱形的公共頂點、20個具有3倍對稱性的頂點,位於6個寬窄交替之菱形的公共頂點上、30個具有2倍對稱性的頂點,位於較窄菱形面的面心和15個鏡像平面。剩下的60個頂點是3個菱形的公共頂點則不是對稱點。[4]
構造
菱形九十面體可以由不均勻的截角二十面體在所有面上加上角錐,並調整錐高直到加入之角錐的側面與鄰面加入之角錐的側面共面或二面角為零為止來構造,並且確保兩種錐體(加入到截角二十面體所有面上的錐體會有五角錐和六角錐兩種)的側邊邊長相等。這種構造方式在康威多面體表示法中記為j,而截角二十面體在康威多面體表示法中記為tI[7],則菱形九十面體在康威多面體表示法中可以表示為jtI。如果構造的過程並未強制讓兩種錐體側邊邊長相等,僅受二十面體對稱性的限制,則所形成之立體中的寬菱形會變成箏形。
在康威多面體表示法中,其可以表示為jtI或dakD[8]。
面的組成
菱形九十面體由兩種菱形組成。其中有60個較寬的菱形和30個較窄的菱形。若菱形九十面體的邊長為單位長,則較寬的菱形寬度為:[1]

較寬的菱形長度為:[1]

較寬的菱形的對角線比為1比2的平方根[9],兩個角分別為r = arccos(1/3) = 70.528779°和R = arccos(-1/3) = 109.471221°。[10][4]
而較窄的菱形寬度為:[1]

較窄的菱形長度為:[1]

較窄的菱形的對角線比為1比黃金比例的平方[9],約為1:2.6180339887;兩個角分別為r' =  = 41.810315°和R' =
= 41.810315°和R' =  = 138.189685°。[10][4]
= 138.189685°。[10][4]
二面角
菱形九十面體有兩種二面角,分別為較窄菱形面與較寬菱形面的二面角,以及較寬菱形面與較寬菱形面的二面角。其中,較窄菱形面與較寬菱形面的二面角約為157.761度:[1]

較寬菱形面與較寬菱形面的二面角約為164.4775度:[1]

尺寸
若菱形九十面體的邊長為單位長,則其體積 和表面積
和表面積 為:[1]
為:[1]
 [1]
[1] [11]
[11]
菱形九十面體的頂點頂並未共球,因此不存在外接球,而其三種頂點分別共球,分別為三階頂點(3個菱形的公共頂點)共球、五階頂點(5個菱形的公共頂點)共球和六階頂點(6個菱形的公共頂點)共球。這些球面的半徑為:[1]
- 三階頂點(3個菱形的公共頂點)共球的球半徑為:[1]

- 五階頂點(5個菱形的公共頂點)共球的球半徑為:[1]

- 六階頂點(6個菱形的公共頂點)共球的球半徑為:[1]

參見
參考文獻
- ^ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 David I. McCooey. Other Solids: Rhombic Enneacontahedron. [2022-08-09]. (原始内容存档于2022-08-09).
- ^ Weisstein, Eric W. (编). Rhombic Enneacontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Robert Webb. Rhombic Enneacontahedron. software3d.com. [2022-08-09]. (原始内容存档于2022-08-09).
- ^ 4.0 4.1 4.2 4.3 George W. Hart. A color-matching dissection of the rhombic enneacontahedron. Symmetry Culture Sci. 2000, 11: 183–199.
- ^ Soma, Takashi and Watanabe, Yasunari. Animation of Some Truncated Polyhedrons. FORMA-TOKYO (Citeseer). 2000, 15 (1): 67–73.
- ^ Jim McNeill. The Rhombic Enneacontahedron and relations. rchidpalms.com. [2022-08-09]. (原始内容存档于2021-12-27).
- ^ Zefiro, Livio. Vertex-and edge-truncation of the Platonic and Archimedean solids leading to vertex-transitive polyhedra. Visual Mathematics (Mathematical Institute SASA). 2011, (50) [2022-08-09]. (原始内容存档于2022-12-07).
- ^ PolyHédronisme. [2022-08-09]. (原始内容存档于2022-03-31).
- ^ 9.0 9.1 Lambert M. Surhone, Mariam T. Tennoe, Susan F. Henssonow. Rhombic Enneacontahedron. Betascript Publishing. 2010-08-18. ISBN 978-613-2-31373-7.
- ^ 10.0 10.1 Richard Klitzing. rhombic enneacontahedron. bendwavy.org. [2022-08-09]. (原始内容存档于2022-08-09).
- ^ Wolfram, Stephen. "rhombic enneacontahedron". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
外部連結