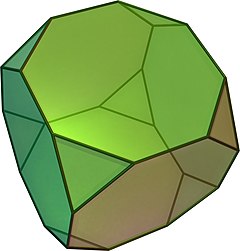
在幾何學 中,截角立方体 是一種十四面體 ,由八個正三角形 與六個正八邊形 組成,具有14個面 、24個頂點 以及36條邊 。是一種阿基米德立體 [ 1] 半正多面體 。其對偶多面體 為三角化八面體 。
截角立方體是一種適當截角 的立方體 。截角時確定了截面的邊與沒截到的長度等長,因此會形成正八邊形 。過度截角到最後會變成截半立方體 。
截角立方體的對偶多面體 是三角化八面體 ,若截角立方體的邊長是2,則其對偶 的邊常會變成
2
+
2
{\displaystyle \scriptstyle {2+{\sqrt {2}}}}
一個邊長為2ξ、幾何中心 位於原點 的截角立方體,其頂點座標為:
(±ξ, ±1, ±1),
(±1, ±ξ, ±1),
(±1, ±1, ±ξ) 其中 ξ =
2
−
1
{\displaystyle \scriptstyle {{\sqrt {2}}-1}}
參數ξ的值可以在±1之間變化。值為1時產生一個立方體、值為0時是截半立方體 ,負值會變成自我相交 的八角星 面。
截角立方體的表面積為
2
(
6
+
6
2
+
3
)
a
2
{\displaystyle 2(6+6{\sqrt {2}}+{\sqrt {3}})a^{2}}
1
3
(
21
+
14
2
)
a
3
{\displaystyle {\frac {1}{3}}(21+14{\sqrt {2}})a^{3}}
a
{\displaystyle a}
[ 2]
表面積 =
A
=
2
(
6
+
6
2
+
3
)
a
2
≈
32.4346644
a
2
{\displaystyle A=2(6+6{\sqrt {2}}+{\sqrt {3}})a^{2}\approx 32.4346644a^{2}}
體積 =
V
=
1
3
(
21
+
14
2
)
a
3
≈
13.5996633
a
3
{\displaystyle V={\frac {1}{3}}(21+14{\sqrt {2}})a^{3}\approx 13.5996633a^{3}}
將立方體 進行截角操作 ,也就是將立方體的八個頂點 切去並在被切掉的地方建立八個正三角形 面即可得到一個截角立方體 。
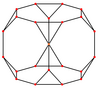
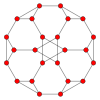
截角立方體具有五個特殊正交投影,可分為三大類:以頂點為中心、以邊緣為中心(稜)、以及以面為中心。以頂點為中心僅有一種,以邊緣(稜)為中心有兩種:以三角形-八邊形邊為中心和以八邊形-八邊形邊為中心;以面為中心也是兩種:以三角形面為中心以及以八邊形面為中心。最後兩個對應B2 和A2 考克斯特平面。
截角立方體的正交投影
建立方式
頂點
邊
邊
面
面
截角立方體
三角化八面體 (對偶多面體)
投影
[2]
[2]
[2]
[4]
[6]
一個被分解的截角立方體 截角立方體可以分割成一個中央立方體、周圍六個四角帳塔 跟角落八個正四面體。這種結構也可以在大斜方截半立方體堆砌中發現,其具有立方體、正四面體以及小斜方截半立方體的胞。
這種分解方式去除兩個四角帳塔 和中間的立方體 可以用來構造斯圖爾特環形所有正的 面,這種「被挖空的」立方體有16個三角形,正方形12,和4個八邊形[ 3] [ 4]
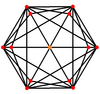
共有三種多面體與截角立方體有著相同的頂點排佈。他們分別為:
截角立方體是立方體經過截角變換 後的結果,與立方體相關的多面體還有:
半正正八面体家族多面体
对称性 : [4,3] , (*432)
[4,3]+ , (432)
[1+ ,4,3], (*332)
[4,3+ ], (3*2)
{4,3}
t0,1 {4,3}
t1 {4,3}
t1,2 {4,3}
{3,4}
t0,2 {4,3}
t0,1,2 {4,3}
s{4,3}
h{4,3}
h1,2 {4,3}
半正多面体的对偶
V4.4.4
V3.8.8
V3.4.3.4
V4.6.6
V3.3.3.3
V3.4.4.4
V4.6.8
V3.3.3.3.4
V3.3.3
V3.3.3.3.3
此多面體的拓撲結構屬於考克斯特對稱群[n,3]構成的一系列頂點配置為(3.2n.2n)和n.8.8的均勻截角多面體和鑲嵌家族的一部分。
截角立方體的面組成方式是一個正八邊形與正三角形交錯組成。同樣由正多邊形與正三角形交錯組成的多面體或鑲嵌圖包括:
如上所述,截角立方體的面組成方式是一個正八邊形與正三角形交錯組成。另外一種就是視為正八邊形與其他正多邊形交錯組成。具有此性質的多面體或鑲嵌圖包括:
截角立方體是將立方體每一個頂點切去,而立方體具有偶數個頂點(8個),且每個面的角數量也是偶數個(正方形有四個角)因此可以進行交錯截角 。交錯截角立方體是一個倒角四面體 。
截角立方體是截角 超方形 家族中的第二個成員,相關的多胞體 包括:
^ Cromwell, P. Polyhedra , CUP hbk (1997), pbk. (1999). Ch.2 p.79-86 Archimedean solids
^ Weisstein, Eric W. (编), Truncated cube , (Archimedean solid) , at MathWorld Wolfram Research, Inc. (英语) ^ B. M. Stewart, Adventures Among the Toroids (1970) ISBN 978-0-686-11936-4
^ 存档副本 . [2016-01-29 ] . (原始内容存档 于2016-02-04).
Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X Cromwell, P. Polyhedra , CUP hbk (1997), pbk. (1999). Ch.2 p.79-86 Archimedean solids
星號*表示該立體屬於
阿基米德立體 。
黃色和紅色為來自原像的面;藍色為截邊出現的正方形面;灰色為扭稜出現的三角形面。