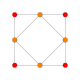
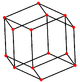
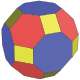
在幾何學 中,截半立方體 是一種十四面體 ,由八個三角形 與六個正方形 組成,具有14個面 、12個頂點 以及24條邊。是一種阿基米德立體 [ 1] 半正多面體 和擬正多面體 。其對偶多面體 為菱形十二面體 。
截半立方體 具有十二個結構相等的頂點 ,皆為兩個三角形與兩個正方形的公共頂點、24個結構相等的稜 ,相鄰面皆為三角形與正方形,兩面角 為反正割 負 根號三 [ 2] 度 ,因此同時具有點可遞和邊可遞的性質,因此是一種均勻多面體 、半正多面體 和擬正多面體 ,並且為阿基米德 發現的13種半正多面體 之一,因此也屬於阿基米德立體 。此外,由於截半立方體可以視為立方體 和其對偶多面體 正八面體 中三角形與正方形的組合,因此又是一種立方體 和其對偶多面體 正八面體 的立體混合物。
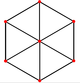
截半立方體形成的四個正六邊形,以顏色分隔 截半立方體 是立方體 透過截半變換 構造而成的多面體,簡而言之是用立方體由一條棱斬到另一條棱的中點(即斬去立方體的頂點)而成。因此其正方形面的數目和立方體的面都為6,其三角形面數目和立方體的頂點數目都為8,共有面14個。因為同樣種類的正多邊形面棱不相交,故可以計算其邊數乘以面的數目來得其棱的數目:3×8=4×6=24。
截半立方體 是立方體 透過截半變換 構造而成的多面體,也可以由對偶——正八面體 透過截半變換 構成[ 3] 截半八面體 。
截半立方體每六條棱可以成為一個正六邊形 ,共有四個獨立的六邊形。
一個邊長 為2的平方根 的截半立方體,其頂點座標位於(0, ±1, ±1)、(±1, 0, ±1)、(±1, ±1, 0)[ 4]
表面積
(
6
+
2
3
)
a
2
{\displaystyle (6+2{\sqrt {3}})~a^{2}}
5
3
2
a
3
{\displaystyle {5 \over 3}{\sqrt {2}}~a^{3}}
a
{\displaystyle a}
[ 2]
表面積 =
(
6
+
2
3
)
a
2
≈
9.4641
a
2
{\displaystyle (6+2{\sqrt {3}})~a^{2}\approx 9.4641~a^{2}}
體積 =
5
3
2
a
3
≈
2.3570
a
3
{\displaystyle {5 \over 3}{\sqrt {2}}~a^{3}\approx 2.3570~a^{3}}
截半立方體的作法有兩種,一種由立方體 出發,另外一種由正八面體出發,同樣都是透過截半變換 來構造。從立方體出發的方法為:將立方體 的八個頂點切到一半就可以得到一個截半立方體,而從正八面體出發的作法一樣是將頂點切到一半:將正八面體 的六個頂點切到一半就可以得到一個截半立方體。
截半立方體的康威多面體記號為aC或aO,由於截半變換 的性質,對偶後結伴得到相同結果,即 a = ad ,因此可以得到 aC (截半立方體) = adC = a(dC) = aO (截半八面體)。
另外也可以由編號3的詹森多面體 ,J3 ——三角帳塔 組成,兩個相反並交錯堆疊,稱為異相雙三角帳塔 ,而另外一種叫做同相雙三角帳塔 ,也是一種詹森多面體 ,編號J27 。
平行十四面體 (英語:Heptaparallelohedron ),在英語 中,Heptaparallelohedron指的是有七組平行面的多面體 ,Hepta-代表七 ,Parallelo-代表平行 ,類似的命名方式例如Parallelogram,指平行四邊形 。Heptaparallelohedron一詞巴克敏斯特·富勒 首次使用代表截半立方體 。
在Oh 對稱性中,可以稱為截半 立方體 截半八面體 (諾曼·約翰遜
在Td 對稱性中,可以稱為小斜方截半 四面體
在D3d 對稱性中,可以稱為異相雙三角帳塔 。
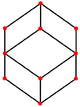
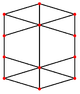
截半立方體的正交投影
正方形
正三角形
頂點
邊
歪斜
[4]
[6]
[2]
[2]
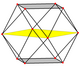
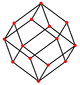
菱形十二面體為截半立方體的對偶
正四面体家族半正多面体
对称性 : [3,3] , (*332)
[3,3]+ , (332)
{3,3}
t0,1 {3,3}
t1 {3,3}
t1,2 {3,3}
t2 {3,3}
t0,2 {3,3}
t0,1,2 {3,3}
s{3,3}
半正多面体对偶
V3.3.3
V3.6.6
V3.3.3.3
V3.6.6
V3.3.3
V3.4.3.4
V4.6.6
V3.3.3.3.3
也可以由倒角立方体 經過特殊的切割方式而得。在切割成截半立方體之前可以得到一些不同的多面體,例如:
半正正八面体家族多面体
对称性 : [4,3] , (*432)
[4,3]+ , (432)
[1+ ,4,3], (*332)
[4,3+ ], (3*2)
{4,3}
t0,1 {4,3}
t1 {4,3}
t1,2 {4,3}
{3,4}
t0,2 {4,3}
t0,1,2 {4,3}
s{4,3}
h{4,3}
h1,2 {4,3}
半正多面体的对偶
V4.4.4
V3.8.8
V3.4.3.4
V4.6.6
V3.3.3.3
V3.4.4.4
V4.6.8
V3.3.3.3.4
V3.3.3
V3.3.3.3.3
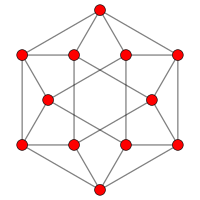
在圖論的數學領域中,與截半立方體相關的圖為截半立方體圖 ,是截半立方體之邊與頂點的圖 阿基米德圖 頂點 和24條稜,且是四次 阿基米德圖 [ 8]
正交投影
^ Cromwell, P. Polyhedra , CUP hbk (1997), pbk. (1999). Ch.2 p.79-86 Archimedean solids
^ 2.0 2.1 Weisstein, Eric W. (编), Cuboctahedron , (Archimedean solid) , at MathWorld Wolfram Research, Inc. (英语) ^ Ghyka, Matila. The geometry of art and life. [Nachdr.] New York: Dover Publications. 1977: 51 –56, 81–84. ISBN 9780486235424 ^ Weisstein, Eric W. Cuboctahedron. CRC Concise Encyclopedia of Mathematics. 2nd. Hoboken: CRC Press: 620–621. 2002. ISBN 9781420035223 ^ 珍.E.霍夫特(Jane E. Hoffelt). 我們住在同一個世界. 大穎【生活學習】. 胡洲賢 譯. 大穎. 2009. ISBN 9789866407758 我們住在同一個世界(培養孩子包容的世界觀)~獲第32次中小學生優良課外讀物推介 互联网档案馆 的存檔 ,存档日期2016-02-04. 戴美心地圖 [2016-1-27]^ 一般性地圖資料代碼 (页面存档备份 ,存于互联网档案馆 ) 國家圖書館 編目 第四頁 dg = 戴美克森氏投影 (dimaxion) 2001年10月^ Vector Equilibrium: R. Buckminster Fuller . [2016-01-27 ] . (原始内容存档 于2016-03-08). ^ Read, R. C.; Wilson, R. J., An Atlas of Graphs, Oxford University Press : 269, 1998
星號*表示該立體屬於
阿基米德立體 。
黃色和紅色為來自原像的面;藍色為截邊出現的正方形面;灰色為扭稜出現的三角形面。