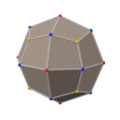
هœ¨ه¹¾ن½•ه¸ ن¸ï¼Œن؛”角ن؛Œهچپه››é¢é«” وک¯ن¸€ç¨®هچ،ه،”èکه¤ڑé¢é«” [ 1] ه°چهپ¶ه¤ڑé¢é«” ç‚؛و‰و£±ç«‹و–¹é«” [ 2] é¢ م€پ60ه€‹é‚ٹ ه’Œ38ه€‹é ‚é» [ 3]
هœ¨ç¤¦ç‰©ه¸ ن¸ï¼Œé€™ç¨®ه½¢ç‹€ هڈˆç¨±ç‚؛ن؛”角ن¸‰ه…«é¢é«” م€پè؛و—‹ن؛Œهچپه››é¢é«” (gyroid)[ 4] [ 5] [ 6] ن؛”角هپڈو–¹ن¸‰ه…«é¢é«” وˆ–هپڈèڈ±ن؛”角ن؛Œهچپه››é¢é«” [ 7] [ 8] 赤éٹ…礦 ——هŒ–ه¸وˆگن»½ç‚؛و°§هŒ–ن؛éٹ… (Cu2 O)çڑ„و°§هŒ–物礦物 هڈ¯ن»¥çµگو™¶وˆگن؛”角ن؛Œهچپه››é¢é«”[ 9]
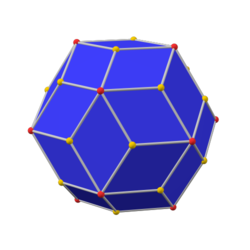
ن؛”角ن؛Œهچپه››é¢é«”وک¯ن¸€ه€‹و‰‹و€§ه¤ڑé¢é«” [ 10] ه¤ڑé¢é«” éڈ،ه°„ ن¹‹ه¾Œوœƒè·ںهژںوœ¬çڑ„ه‹ه½¢ç‹€ن¸چهگŒï¼Œç„،و³•è—‰ç”±و—‹è½‰ هچٹه‘¨ه†چه›هˆ°هژںوœ¬çڑ„ه½¢ç‹€[ 11] [ 12] [ 13] و‰‹و€§ éڈ،هƒڈ,ن¸”ه…¶é¢ م€پé ‚é» م€پé‚ٹ و•¸çڑ†ç›¸هگŒï¼Œه…±وœ‰24ه€‹é¢ م€پ60ه€‹é‚ٹ م€پ38ه€‹é ‚é» [ 3]
ن؛”角ن؛Œهچپه››é¢é«” çڑ„و—‹è½‰é€ڈ視هœ–
ن؛”角ن؛Œهچپه››é¢é«” çڑ„هڈ¦ن¸€ه€‹و‰‹و€§ éڈ،هƒڈçڑ„و—‹è½‰é€ڈ視هœ–
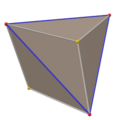
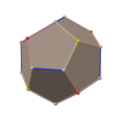
ن؛”角ن؛Œهچپه››é¢é«”çڑ„ه°چهپ¶ه¤ڑé¢é«” ç‚؛و‰و£±ç«‹و–¹é«” ,وڈ›هڈ¥è©±èھھهچ³é€™ه€‹ه¤ڑé¢é«”çڑ„é ‚é»هڈ¯ن»¥ه°چو‡‰هˆ°و‰و£±ç«‹و–¹é«”و¯ڈه€‹é¢çڑ„ه¹¾ن½•ن¸ه؟ƒم€پو‰و£±ç«‹و–¹é«”çڑ„و¯ڈه€‹é ‚é»هڈ¯ن»¥ه°چو‡‰هˆ°ن؛”角ن؛Œهچپه››é¢é«”çڑ„ه¹¾ن½•ن¸ه؟ƒ م€‚[ 14]
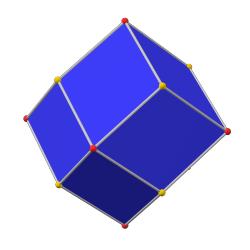
و§‹وˆگن؛”角ن؛Œهچپه››é¢é«”çڑ„ن؛”é‚ٹه½¢م€‚ ن؛”角ن؛Œهچپه››é¢é«”ç”±24ه€‹ه…¨ç‰çڑ„ه…·وœ‰éڈ،هƒڈه°چ稱و€§ن¹‹ن¸چç‰é‚ٹن؛”é‚ٹه½¢çµ„وˆگ[ 13] [ 12] ن¸‰و³¢é‚£ه¥‘ه¸¸و•¸ [ 15]
çںé‚ٹ
:
{\displaystyle :}
=
1
:
1
2
+
t
2
{\displaystyle =1:{\frac {1}{2}}+{\frac {t}{2}}}
ه…¶ن¸ï¼Œ
t
{\displaystyle t}
ن¸‰و³¢é‚£ه¥‘ه¸¸و•¸
1
+
19
+
3
33
3
+
19
−
3
33
3
3
=
1
+
4
cosh
(
1
3
cosh
−
1
(
2
+
3
8
)
)
3
≈
1.839286755214161
,
{\displaystyle {\frac {1+{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}}{3}}={\frac {1+4\cosh \left({\frac {1}{3}}\cosh ^{-1}\left(2+{\frac {3}{8}}\right)\right)}{3}}\approx 1.839286755214161,}
OEIS و•¸هˆ—A058265 )這ه€‹و•¸ç‚؛
x
3
−
x
2
−
x
−
1
=
0
{\displaystyle x^{3}-x^{2}-x-1=0}
[ 16]
這ه€‹ن¸چç‰é‚ٹن؛”é‚ٹه½¢ه…©ه€‹é•·é‚ٹ相鄰,ه…¶ه¤¾è§’ç‚؛ن؛Œو¸›هژ»ن¸‰و³¢é‚£ه¥‘ه¸¸و•¸çڑ„هڈچé¤که¼¦ ه€¼ï¼ˆ
arccos
(
2
−
t
)
{\displaystyle \arccos {\left(2-t\right)}}
هڈچé¤که¼¦ ه€¼ï¼ˆ
arccos
(
1
2
−
t
2
)
{\displaystyle \arccos {\left({\tfrac {1}{2}}-{\tfrac {t}{2}}\right)}}
[ 15]
è‹¥ه°چو‡‰çڑ„ه°چهپ¶ه¤ڑé¢é«”——و‰و£±ç«‹و–¹é«” é‚ٹé•·ç‚؛ه–®ن½چ長,ه‰‡ç›¸و‡‰çڑ„ن؛”角ن؛Œهچپه››é¢é«”é¢çڑ„çںé‚ٹé‚ٹé•·ç‚؛[ 13] [ 12]
b
=
6
(
4
−
2
(
13
+
3
33
)
3
−
2
(
13
−
3
33
)
3
)
6
≈
0.593465355971987310502
{\displaystyle b={\frac {\sqrt {6\left(4-{\sqrt[{3}]{2\left(13+3{\sqrt {33}}\right)}}-{\sqrt[{3}]{2\left(13-3{\sqrt {33}}\right)}}\right)}}{6}}\approx 0.593465355971987310502}
相و‡‰çڑ„ن؛”角ن؛Œهچپه››é¢é«”é¢çڑ„é•·é‚ٹé‚ٹé•·ç‚؛[ 13] [ 12]
a
=
3
(
4
+
19
+
3
33
3
+
19
−
3
33
3
)
6
≈
0.8425091624448604672504
{\displaystyle a={\frac {\sqrt {3\left(4+{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}\right)}}{6}}\approx 0.8425091624448604672504}
è‹¥ه°چو‡‰çڑ„ه°چهپ¶ه¤ڑé¢é«”——و‰و£±ç«‹و–¹é«” é‚ٹé•·ç‚؛ه–®ن½چ長,ه‰‡ç›¸و‡‰çڑ„ن؛”角ن؛Œهچپه››é¢é«”çڑ„é«”ç©چ與è،¨é¢ç©چç‚؛[ 10]
A
=
3
22
(
5
t
−
1
)
4
t
−
3
≈
19.299
94
V
=
11
(
t
−
4
)
2
(
20
t
−
37
)
≈
7.4474
{\displaystyle {\begin{aligned}A&=3{\sqrt {\frac {22(5t-1)}{4t-3}}}&&\approx 19.299\,94\\V&={\sqrt {\frac {11(t-4)}{2(20t-37)}}}&&\approx 7.4474\end{aligned}}}
而و ¹و“ڑ相و‡‰çڑ„é‚ٹé•·é—œن؟‚[ 13] [ 12]
A
=
24
a
2
(
2
+
3
t
)
1
+
2
t
1
−
t
1
+
t
=
12
b
2
(
2
+
3
t
)
(
1
−
2
t
2
)
1
−
t
2
≈
27.19
a
2
≈
54.8
b
3
{\displaystyle A={\frac {24a^{2}(2+3t)}{1+2t}}{\sqrt {\frac {1-t}{1+t}}}={\frac {12b^{2}(2+3t)}{(1-2t^{2})}}{\sqrt {1-t^{2}}}\approx 27.19a^{2}\approx 54.8b^{3}}
V
=
4
a
3
(
2
+
3
t
)
1
−
2
t
(
1
+
t
)
(
1
−
4
t
2
)
=
2
b
3
(
1
+
t
)
(
2
+
3
t
)
(
1
−
2
t
2
)
1
−
2
t
≈
12.45
a
3
≈
35.63
b
3
{\displaystyle V={\frac {4a^{3}(2+3t){\sqrt {1-2t}}}{(1+t)(1-4t^{2})}}={\frac {2b^{3}(1+t)(2+3t)}{(1-2t^{2}){\sqrt {1-2t}}}}\approx 12.45a^{3}\approx 35.63b^{3}}
ن؛”角ن؛Œهچپه››é¢é«”وœ‰ن¸‰ç¨®ه…·وœ‰ç‰¹و®ٹه°چ稱و€§çڑ„و£ن؛¤وٹ•ه½±ï¼Œهˆ†هˆ¥وک¯ن»¥ه؛¦ ç‚؛ن¸‰çڑ„é ‚é»ç‚؛ن¸ه؟ƒم€پن»¥ه؛¦ ç‚؛ه››çڑ„é ‚é»ç‚؛ن¸ه؟ƒن»¥هڈٹن»¥èˆ‡هپ´é‚ٹن¸é»ç‚؛ن¸ه؟ƒçڑ„و£ن؛¤وٹ•ه½±م€‚ه‰چه…©è€…ه°چ稱و€§ه°چهˆ†هˆ¥و‡‰و–¼A2 ه’ŒB2 çڑ„考ه…‹و–¯ç‰¹ه¹³é¢[ 17] [ 18]
و£ن؛¤وٹ•ه½±
وٹ•ه½±ن½چç½®
ه؛¦ ç‚؛ن¸‰çڑ„é ‚é»
ه؛¦ ç‚؛ه››çڑ„é ‚é»
هپ´é‚ٹن¸é»
وٹ•ه½±ه°چ稱و€§
[3]
[4]+
[2]
هœ–هƒڈ
ه°چهپ¶ه¤ڑé¢é«”
ن؛”角ن؛Œهچپه››é¢é«”وœ‰هڈ¦ه¤–ن¸€ç¨®هگŒو¨£و‰€وœ‰é¢ه…¨ç‰çڑ„è®ٹé«”م€‚這種è®ٹé«”ه…·وœ‰ه…«é¢é«”群çڑ„ه°چ稱و€§ï¼Œن¸”ه…·وœ‰3種ن¸چهگŒçڑ„é‚ٹé•·م€‚這種è®ٹé«”هڈ¯ن»¥é€ڈéپژهœ¨و‰و£±ç«‹و–¹é«” çڑ„6ه€‹و£و–¹ه½¢èˆ‡8ه€‹ن¸‰è§’ه½¢çڑ„é¢ن¸ٹهٹ ن¸ٹ角éŒگ至與鄰é¢ه…±é¢ن¾†و§‹é€ [ 19]
و‰و£±ç«‹و–¹é«” çڑ„é¢ن¸ٹهٹ ن¸ٹ角éŒگ至與鄰é¢ه…±é¢
ن؛”角ن؛Œهچپه››é¢é«”çڑ„و‹“و¨¸çµگو§‹ه±¬و–¼(432)çڑ„و—‹è½‰ه°چ稱و€§[ 20]
é—œو–¼çڑ„و‹“و¨¸çµگو§‹ه±¬و–¼(432)çڑ„و—‹è½‰ه°چ稱و€§çڑ„ن؛”角ن؛Œهچپه››é¢é«”[ 20]
ن؛”角ن؛Œهچپه››é¢é«”وک¯ç«‹و–¹é«”經éپژو‰و£±è®ٹوڈ›ه¾Œçڑ„ه°چهپ¶ه¤ڑé¢é«” [ 10]
ه°چ稱و€§ (*432) [4,3]+
[1+ ,4,3] = [3,3](*332)
[3+ ,4](3*2)
{4,3}
t{4,3}
r{4,3} 1,1 }
t{3,4} 1,1 }
{3,4} 1,1 }
rr{4,3} 2 {3,4}
tr{4,3}
c{4,3}
sr{4,3}
h{4,3} h2 {4,3} s{3,4} 1,1 }
ه°چهپ¶ه¤ڑé¢é«”
V43
V3.82
V(3.4)2
V4.62
V34
V3.43
V4.6.8
V4.62 /63
V34 .4
V33
V3.62
V35
هœ¨هœ–è«– çڑ„و•¸ه¸é کهںںن¸ï¼Œèˆ‡ن؛”角ن؛Œهچپه››é¢é«”相關çڑ„هœ–ç‚؛ن؛”角ن؛Œهچپه››é¢é«”هœ– ,وک¯ن؛”角ن؛Œهچپه››é¢é«”ن¹‹é‚ٹèˆ‡é ‚é»çڑ„هœ– ç¯€é» ه’Œ60و¢é‚ٹ組وˆگ[ 21] ه“ˆه¯†é،؟ه›¾ [ 22]
ن؛”角ن؛Œهچپه››é¢é«”هœ–وœ‰60و¢é‚ٹه’Œ38ه€‹é ‚é» ï¼Œه…¶ن¸ه؛¦ ç‚؛3çڑ„é ‚é»وœ‰32ه€‹ï¼›ه؛¦ ç‚؛4çڑ„é ‚é»وœ‰6ه€‹م€‚這ه€‹هœ–çڑ„ç›´ه¾‘وک¯7,هچٹه¾‘وک¯6[ 22] [ 23] ه¾ھç’° è·¯ه¾‘ن¸‹é ‚é»é–“وœ€ه¤§è·é›¢هڈھه°‘相è·6ه€‹é ‚é»ï¼Œوœ€é•·è·é›¢ن¸چ超éپژ7ه€‹é ‚é»[ 22] هœچé•· ç‚؛5,هچ³هœ¨é€™ه€‹هœ–ه…§وœ€ه°ڈçڑ„ه¾ھç’° è·¯ه¾‘ç‚؛5ه€‹é ‚é»[ 22]
و–½èژ±و ¼ه°”ه›¾ ن؛”角ن؛Œهچپه››é¢é«”هœ– çڑ„هڈ¦ن¸€ç¨®è،¨ç¤؛و³•
ن؛”角ن؛Œهچپه››é¢é«”هœ–çڑ„特ه¾µه¤ڑé …ه¼ڈ ç‚؛[ 22]
(
x
−
2
)
2
(
x
−
1
)
3
x
(
x
2
−
x
−
7
)
(
x
2
+
x
−
3
)
(
x
2
+
2
x
−
1
)
2
(
x
3
−
4
x
+
1
)
3
(
x
5
+
x
4
−
8
x
3
−
9
x
2
+
7
x
+
4
)
3
{\displaystyle (x-2)^{2}(x-1)^{3}x(x^{2}-x-7)(x^{2}+x-3)(x^{2}+2x-1)^{2}(x^{3}-4x+1)^{3}(x^{5}+x^{4}-8x^{3}-9x^{2}+7x+4)^{3}}
Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X
^ The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 287, pentagonal icosikaitetrahedron)^ Wenninger, Magnus , Dual Models, Cambridge University Press , 1983, ISBN 978-0-521-54325-5MR 730208 ^ 3.0 3.1 Pentagonal Icositetrahedron . polyhedra.org. [2020-08-01 ] . (هژںه§‹ه†…ه®¹ هکو،£ن؛ژ2008-07-14). ^ Promorphology of Crystals I . www.metafysica.nl. [2020-08-03 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2020-08-03). ^ Stephen A. Nelson. Crystal Form, Zones, Crystal Habit . 2011-01-11 [2020-08-03 ] . (هژںه§‹ه†…ه®¹ هکو،£ن؛ژ2013-09-01). ^ ن؛”角ن¸‰ه…«é¢é«”;è؛و—‹ن؛Œهچپه››é¢é«” gyroid . هœ‹ه®¶و•™è‚²ç ”究院 . [2020-08-01 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2020-08-24). ^ هپڈèڈ±ن؛”角ن؛Œهچپه››é¢é«” pentagonal icositetrahedron . هœ‹ه®¶و•™è‚²ç ”究院 . [2020-08-01 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2020-08-24). ^ ن¸ه·ه®ڈ 貫ه…¥هڈŒو™¶و¨،ه‹مپ®è£½ن½œ (PDF) . [2018-08-30 ] . (هژںه§‹ه†…ه®¹ (PDF) هکو،£ن؛ژ2018-08-31). ^ Hugo Steinhaus. Mathematical Snapshots (Dover Recreational Math) . Dover Publications. 2011ه¹´12وœˆ28و—¥: pp. 207, 209. ISBN 978-0486409146 ^ 10.0 10.1 10.2 Weisstein, Eric W. (ç¼–). Pentagonal Icositetrahedron . at MathWorld Wolfram Research, Inc. (英è¯ï¼‰ . ^ Coxeter, H. S. M. , Kaleidoscopes: Selected Writings , John Wiley and Sons: 282, 1995, ISBN 9780471010036 ^ 12.0 12.1 12.2 12.3 12.4 Catalan Solids: Pentagonal Icositetrahedron (dextro) . dmccooey.com. [2020-08-01 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2020-08-24). ^ 13.0 13.1 13.2 13.3 13.4 Catalan Solids: Pentagonal Icositetrahedron (laevo) . dmccooey.com. [2020-08-01 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2020-08-24). ^ Holden, A. Shapes, Space, and Symmetry . Dover Books on Mathematics. Dover Publications. 1991: p.55. ISBN 9780486268514LCCN 91020471 ^ 15.0 15.1 Pentagonal icositetrahedron . fillygons.ch. [2020-08-01 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2020-08-24). ^ Sloane, N.J.A. (ç¼–). Sequence A058265 (Decimal expansion of the tribonacci constant t, the real root of
x
3
−
x
2
−
x
−
1
{\displaystyle x^{3}-x^{2}-x-1}
. The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. ^ ç´„ç؟°آ·هڈ²ه¦ه¸ƒé‡Œه¥‡ Coxeter Planes . math.lsa.umich.edu. [2020-08-01 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2018-02-10) (英è¯ï¼‰ . ^ ç´„ç؟°آ·هڈ²ه¦ه¸ƒé‡Œه¥‡ More Coxeter Planes . math.lsa.umich.edu. [2020-08-01 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2017-08-21) (英è¯ï¼‰ . ^ Koca, Nazife and Koca, Mehmet. Regular and Irregular Chiral Polyhedra from Coxeter Diagrams via Quaternions. Symmetry. 2017-08, 9 : 148. doi:10.3390/sym9080148 ^ 20.0 20.1 Livio Zefiro, Maria Rosa Ardigo. What Became of the Controversial Fourteenth Archimedean Solid, the Pseudo Rhomb-Cuboctahedron? . Dip.Te.Ris, Universita' di Genova, Italy. [2020-08-24 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2020-07-31). ^ Hao, Jianqiang and Gong, Yunzhan and Sun, Jianzhi and Tan, Li. Use the K-Neighborhood Subgraphs to Compute Canonical Labelings of Graphs. Mathematics (Multidisciplinary Digital Publishing Institute). 2019, 7 (8): 690. ^ 22.0 22.1 22.2 22.3 22.4 Weisstein, Eric W. (ç¼–). Pentagonal Icositetrahedral Graph . at MathWorld Wolfram Research, Inc. (英è¯ï¼‰ . ^ Chartrand G., Johns G., Oellermann O.R. On Peripheral Vertices in Graphs. Bodendiek R., Henn R. (ç¼–). Topics in Combinatorics and Graph Theory. Physica-Verlag HD. 1990.












![{\displaystyle {\frac {1+{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}}{3}}={\frac {1+4\cosh \left({\frac {1}{3}}\cosh ^{-1}\left(2+{\frac {3}{8}}\right)\right)}{3}}\approx 1.839286755214161,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35d67dcf371181e0d9563c8328e2642102ddcce3)




![{\displaystyle b={\frac {\sqrt {6\left(4-{\sqrt[{3}]{2\left(13+3{\sqrt {33}}\right)}}-{\sqrt[{3}]{2\left(13-3{\sqrt {33}}\right)}}\right)}}{6}}\approx 0.593465355971987310502}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b65438f953d1db2cfd40bb40bf2a66ca3b9a971)
![{\displaystyle a={\frac {\sqrt {3\left(4+{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}\right)}}{6}}\approx 0.8425091624448604672504}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1129f13464cb168fe4aa39b33de7613e3983d9df)