在第三个平面(粉红色)中的两个平面(α,β,绿色)之间的角度以直角切割相交线 二面角 (英語:dihedral angle )是两个相交平面之间的夹角。在立体几何 中,它被定义为一条直线 和两个半平面的并集 ,这条直线是两个半平面的公共边 。在高维 中,二面角表示两个超平面 之间的夹角。[ 1]
在化学 中,二面角是分子中的两个分别由三个原子组成的平面之间的夹角,一共涉及四个原子,公共边是一个化学键 (两个原子),平面则由另两个原子分别与该化学键构成。
一条直线 和两个半平面的并集 组成的图形叫做二面角 ,这条直线叫做二面角的棱 ,这两个半平面叫做二面角的面 。
由直线
l
{\displaystyle l}
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
α
−
l
−
β
{\displaystyle \alpha -l-\beta }
2
∠
l
{\displaystyle ^{2}\angle l}
也可在直线
l
{\displaystyle l}
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
P
{\displaystyle P}
Q
{\displaystyle Q}
P
−
l
−
Q
{\displaystyle P-l-Q}
在 二面角
α
−
l
−
β
{\displaystyle \alpha -l-\beta }
l
{\displaystyle l}
O
{\displaystyle O}
O
{\displaystyle O}
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
O
A
{\displaystyle OA}
O
B
{\displaystyle OB}
l
{\displaystyle l}
O
A
{\displaystyle OA}
O
B
{\displaystyle OB}
∠
A
O
B
{\displaystyle \angle AOB}
二面角的平面角 。[ 2]
建立二面角的平面角 在非解析几何方法中,常通过建立二面角的平面角,通过求出平面角的大小,来求出二面角的大小:
∵
A
B
⊥
O
B
{\displaystyle \because AB\perp OB}
∴
O
B
{\displaystyle \therefore OB}
O
A
{\displaystyle OA}
β
{\displaystyle \beta }
射影 。
∵
O
A
⊥
l
,
O
B
⊥
l
{\displaystyle \because OA\perp l,OB\perp l}
∴
∠
A
O
B
{\displaystyle \therefore \angle AOB}
α
−
l
−
β
{\displaystyle \alpha -l-\beta }
若两个相交平面在笛卡尔坐标 中的方程分别为
a
1
x
+
b
1
y
+
c
1
z
+
d
1
=
0
{\displaystyle a_{1}x+b_{1}y+c_{1}z+d_{1}=0}
a
2
x
+
b
2
y
+
c
2
z
+
d
2
=
0
,
{\displaystyle a_{2}x+b_{2}y+c_{2}z+d_{2}=0\,\,,}
则它们之间的二面角
φ
{\displaystyle \varphi }
cos
φ
=
|
a
1
a
2
+
b
1
b
2
+
c
1
c
2
|
a
1
2
+
b
1
2
+
c
1
2
a
2
2
+
b
2
2
+
c
2
2
.
{\displaystyle \cos \varphi ={\frac {\left\vert a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}\right\vert }{{\sqrt {a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}}{\sqrt {a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}}}\,\,.}
另一种方法是计算两个平面的法向量 n A 和n B 之间的夹角:
cos
φ
=
|
n
A
⋅
n
B
|
|
n
A
|
|
n
B
|
,
{\displaystyle \cos \varphi ={\frac {\left\vert \mathbf {n} _{\mathrm {A} }\cdot \mathbf {n} _{\mathrm {B} }\right\vert }{|\mathbf {n} _{\mathrm {A} }||\mathbf {n} _{\mathrm {B} }|}}\,\,,}
其中n A • n B 是两个向量的点积 ,|n A | |n B |是两个向量的模 的乘积。[ 3]
任何平面也可以由位于该平面的两个非共线向量来描述;他们的叉积 是平面的法向量。因此,二面角可以由三个向量b 1 、b 2 和b 3 定义,形成两对非共线向量:[ 4]
φ
=
atan2
(
(
[
b
1
×
b
2
]
×
[
b
2
×
b
3
]
)
⋅
b
2
|
b
2
|
,
[
b
1
×
b
2
]
⋅
[
b
2
×
b
3
]
)
,
{\displaystyle \varphi =\operatorname {atan2} \left({\big (}[\mathbf {b} _{1}\times \mathbf {b} _{2}]\times [\mathbf {b} _{2}\times \mathbf {b} _{3}]{\big )}\cdot {\frac {\mathbf {b} _{2}}{|\mathbf {b} _{2}|}}\,\,,\,\,[\mathbf {b} _{1}\times \mathbf {b} _{2}]\cdot [\mathbf {b} _{2}\times \mathbf {b} _{3}]\right)\,\,,}
其中atan2 是二個參數的反正切函數 變體,一般而言,atan2(y, x) 等價於 atan(y/x)。
正丁烷的自由能图作为二面角的函数 在化学 中,扭转角 (英語:torsion angle )被定义为二面角的特定例子,描述了通过化学键 连接的分子的两个部分的几何关系。[ 5] [ 6]
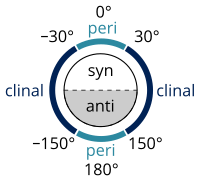
在立体化学 中,分子 中的每三个(非共线)原子都决定了一个平面。当两个这样的平面相交时,它们之间的角度便是二面角。二面角用于描述具体的分子构象 [ 7] syn (s,顺);在±90°和180°之间的为anti (a,反)。类似地,角度在30°和150°之间或-30°和-150°之间的被称为clinal (c,错),而在0°和±30°或±150°和180°之间的被称为periplanar (p,叠)。
这两种术语可以组合起来,以定义四个角度范围:0°至±30°为顺叠(sp);30°至90°和-30°至-90°为顺错(sc);90°至150°和-90°至-150°为反错(ac);±150°至180°为反叠(ap)。顺叠构象也被称为顺式(syn -或cis -)构象;反叠构象也被称为反式(anti -或trans -)构象;顺错构象也被称为邻位交叉 、間扭(gauche 或skew )构象。
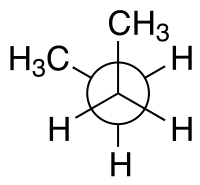
例如,对于正丁烷 ,可以用两个中心碳原子和任一个甲基碳原子来分别指定两个平面。本节开头(上图)所示的syn -构象具有60°的二面角,比180°二面角的anti -构象更不稳定。
对于大分子使用,建议使用符号T,C,G+ ,G- ,A+ 和A- 分别表示ap,sp,+sc,-sc,+ac和-ac。[ 5]
描述蛋白质,显示骨架二面角 拉氏图(也称为Ramachandran图或[φ ,ψ ]图),由G·N·Ramachandran、C·Ramakrishnan和V·Sasisekharan在1963年最初开发[ 8] 蛋白质结构 中能量(位阻)允许的氨基酸 残基的二面角ψ 与φ 的关系的方式。右图展示了骨架二面角φ 和ψ 的定义[ 9] φ 和φ' )。
在蛋白质 链中,三个二面角被定义为φ (phi),ψ (psi)和ω (omega),如图所示。肽键 的平面性通常使得ω 被限制为180°(典型trans 情况)或0°(罕见cis 情况)。trans 和cis 异构体的α-碳 之间的距离分别为大约3.8和2.9 Å。cis 异构体主要在Xaa-Pro 肽键(其中Xaa是任何氨基酸 )中观察到。
侧链二面角倾向于聚集在180°,60°和-60°附近,称为trans ,gauche+ 和gauche- 构象。某些侧链二面角的稳定性受到φ 和ψ 值的影响[ 10] ψ 接近-60°时,gauche+ 旋转异构体的侧链中的γ-碳 和下一个残基的氮之间就会有直接的位阻 相互作用[ 11]
在聚合物特别是蛋白质中,常常用内部坐标来描述主链,也即把二面角和键长按照顺序列表。但是,某些类型的计算化学 反而使用笛卡尔坐标 。在计算结构优化中,一些程序需要在迭代过程中在这些表示法之间来回转换,这项工作可能占用大部分计算时间。对于有很多迭代或长链的过程,它也可能引入累积的数值不准确性。虽然所有的转换算法会产生数学上相同的结果,但它们的运算速度和数字精度不同。[ 12] [需要非第一手來源]
每个多面体在每条边上都有一个二面角,用于描述以该边为公共边的两个面的关系。该二面角也被称为面角 ,其计算的是多面体的内角。面角0°意味着两个面法向量是反向平行的,而且两个面相互重叠,这意味着它是退化多面体的一部分。面角为180°意味着这些面是平行的,如在镶嵌中。在多面体的凹部,可以存在大于180°的面角,在基础数学二面角的取值范围上有争议目前认为取值为[0,180]。
边传递多面体中的每个二面角大小相同。这包括5个正多面体 ,4个星型正多面体,两个拟正多面体和两个拟正对偶多面体。
给定一个在共同顶点 P上相交且具有边AP、BP和CP的多面体的三个面,包含APC和BPC的面之间的二面角的余弦为:[ 13]
cos
φ
=
cos
(
∠
A
P
B
)
−
cos
(
∠
A
P
C
)
cos
(
∠
B
P
C
)
sin
(
∠
A
P
C
)
sin
(
∠
B
P
C
)
.
{\displaystyle \cos \varphi ={\frac {\cos(\angle \mathrm {APB} )-\cos(\angle \mathrm {APC} )\cos(\angle \mathrm {BPC} )}{\sin(\angle \mathrm {APC} )\sin(\angle \mathrm {BPC} )}}\,\,.}
^ Olshevsky, George, Dihedral angle Glossary for Hyperspace .
^ 2.3.2平面与平面垂直的判定. 普通高中课程标准实验教科书 数学2 必修 A版. 普通高中课程标准实验教科书 数学2 必修 A版: 68. ISBN 978-7-107-17706-4 ^ Angle Between Two Planes . TutorVista.com. [2018-07-06 ] . (原始内容存档 于2020-10-28). 页面存档备份 ,存于互联网档案馆 )^ Blondel, Arnaud; Karplus, Martin. New formulation for derivatives of torsion angles and improper torsion angles in molecular mechanics: Elimination of singularities . Journal of Computational Chemistry. 7 Dec 1998, 17 (9): 1132–1141 [2018-07-08 ] . doi:10.1002/(SICI)1096-987X(19960715)17:9<1132::AID-JCC5>3.0.CO;2-T 存档 于2018-02-03). 页面存档备份 ,存于互联网档案馆 )^ 5.0 5.1 國際純化學和應用化學聯合會 ,化學術語概略 Torsion angle "。doi :10.1351/goldbook.T06406 ^ 國際純化學和應用化學聯合會 ,化學術語概略 Dihedral angle "。doi :10.1351/goldbook.D01730 ^ Anslyn, Eric; Dennis Dougherty. Modern Physical Organic Chemistry. University Science. 2006: 95. ISBN 978-1891389313 ^ Ramachandran, G. N.; Ramakrishnan, C.; Sasisekharan, V. Stereochemistry of polypeptide chain configurations. Journal of Molecular Biology. 1963, 7 : 95–9. PMID 13990617 doi:10.1016/S0022-2836(63)80023-6 ^ Richardson, J. S. Anatomy and Taxonomy of Protein Structures. Advances in Protein Chemistry. Advances in Protein Chemistry. 1981, 34 : 167–339. ISBN 9780120342341PMID 7020376 doi:10.1016/S0065-3233(08)60520-3 ^ Dunbrack, RL Jr.; Karplus, M. Backbone-dependent rotamer library for proteins. Application to side-chain prediction.. Journal of Molecular Biology. 20 March 1993, 230 (2): 543–74. PMID 8464064 doi:10.1006/jmbi.1993.1170 ^ Dunbrack, RL Jr; Karplus, M. Conformational analysis of the backbone-dependent rotamer preferences of protein sidechains.. Nature Structural Biology. May 1994, 1 (5): 334–40. PMID 7664040 doi:10.1038/nsb0594-334 ^ Parsons, J.; Holmes, J. B.; Rojas, J. M.; Tsai, J.; Strauss, C. E., Practical conversion from torsion space to cartesian space for in silico protein synthesis, Journal of Computational Chemistry, 2005, 26 : 1063–1068, PMID 15898109 doi:10.1002/jcc.20237 ^ dihedral angle calculator polyhedron . www.had2know.com. [2015-10-25 ] . (原始内容 存档于2015-11-25). 页面存档备份 ,存于互联网档案馆 )

























![{\displaystyle \varphi =\operatorname {atan2} \left({\big (}[\mathbf {b} _{1}\times \mathbf {b} _{2}]\times [\mathbf {b} _{2}\times \mathbf {b} _{3}]{\big )}\cdot {\frac {\mathbf {b} _{2}}{|\mathbf {b} _{2}|}}\,\,,\,\,[\mathbf {b} _{1}\times \mathbf {b} _{2}]\cdot [\mathbf {b} _{2}\times \mathbf {b} _{3}]\right)\,\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f704b95fc0762659534b089d581fe952f6de7af)