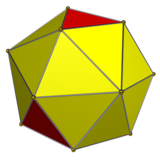
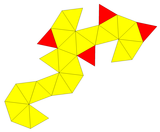
截角三角化四面體 (truncated triakis tetrahedron )或更精確地稱為截六階角三角化四面體 (order-6 truncated triakis tetrahedron )是一種凸 十六面體 ,由12個五邊形 和4個六邊形 所組成[ 1] 五邊形 ,每組有三個,並以四面體 的邊 和面 之關係排列,原屬於四面體 頂點的部分在此立體中則為六邊形 。
截角三角化四面體的旋轉模型 一些化學物質的晶格 之原子排列方式能構成截角三角化四面體。[ 2]
截六階角三角化四面體可以透過截去三角化四面體 的6個六階頂點(六面角)來構造,這個動作建立了4個正六邊形 ,並留下12個鏡像對稱的五邊形 。
三角化四面體 拓撲結構類似的等邊多面體 可以通過使用12個正五邊形、4個等邊但非平面六邊形來構造,每個頂點與內部的角度在108度和132度之間的交替。
由於其大部分的面十分接近正多邊形,因此也被歸類為擬詹森多面體 [ 3]
截角三角化四面體可以分成三種形式,一種是標準的截角 形式,這種形式有兩種邊長,短邊長與長邊長的比為
3
+
3
5
{\displaystyle {\frac {3+{\sqrt {3}}}{5}}}
[ 4]
3
(
5
+
3
)
22
{\displaystyle {\frac {3\left(5+{\sqrt {3}}\right)}{22}}}
[ 5] [ 註 2] 外接球 的形式,也就是所有頂點共球的形式,在這種形式中,短邊長與長邊長的比為
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
[ 6] [ 註 4]
標準的截角形式之截角三角化四面體,若其長邊長為單位長,則其體積 為:[ 4] [ 7] :483
111
2
+
50
6
20
≈
13.9726
{\displaystyle {\frac {111{\sqrt {2}}+50{\sqrt {6}}}{20}}\approx 13.9726}
五邊形面由1長邊和4短邊組成的截角三角化四面體,若其短邊長為單位長,則其體積為:[ 5]
125
2
+
39
6
18
≈
15.128155
{\displaystyle {\frac {125{\sqrt {2}}+39{\sqrt {6}}}{18}}\approx 15.128155}
存在外接球的形式之截角三角化四面體,若其外接球半徑為單位長,則其體積為:[ 6]
1288
3
729
≈
3.060194
{\displaystyle {\frac {1288{\sqrt {3}}}{729}}\approx 3.060194}
截三階角三角化四面體 三角化四面體一共有兩種頂點,分別為6階頂點和3階頂點;屬於擬詹森多面體的截角三角化四面體僅截去了6階頂點,因此又稱為截六階角三角化四面體。另一種截三階角三角化四面體則是截去3階頂點的截角三角化四面體,稱為截三階角三角化四面體(order-3 truncated triakis tetrahedron )。
截三階角三角化四面體的外觀為每個面疊上三角錐台 的四面體,由12個梯形和4個三角形組成,也是一種十六面體 。
其對偶多面體為三角化截角四面體 空間填充多面體 [ 8] [ 9]
三角化四面體一共有兩種頂點,分別為6階頂點和3階頂點;屬於擬詹森多面體的截角三角化四面體僅截去了6階頂點,因此又稱為截六階角三角化四面體。真正的截角三角化四面體是指將6階頂點和3階頂點全部截去的三角化四面體,截完後的結果是一個不規則的二十面體 。
六角化截角四面體的旋轉模型 截六階角三角化四面體的對偶多面體稱為六角化截角四面體,其可以透過在截角四面體的每個六邊形上疊上六角錐 構成。
六角化截角四面體無法成為詹森多面體,因為若要保持所有面都是正多邊形時,在截角四面體的每個六邊形上疊上的六角錐 之側面 會互相共面而成為非嚴格凸的多面體。
若截角四面體疊上的六角錐 之頂點正好位於其外接球,則當截角四面體的邊長為單位長時,六角錐 的側面三角形的腰長為:[ 10]
11
−
33
2
≈
1.146237
{\displaystyle {\frac {\sqrt {11-{\sqrt {33}}}}{2}}\approx 1.146237}
^ Wolfram, Stephen . " 3/(5-sqrt(3))" Wolfram Alpha : Computational Knowledge Engine, Wolfram Research (英语) . ^ 來源給出的結果為長邊長為
5
−
3
3
{\displaystyle {\frac {5-{\sqrt {3}}}{3}}}
[ 5]
5
−
3
3
{\displaystyle {\frac {5-{\sqrt {3}}}{3}}}
5
−
3
3
{\displaystyle {\frac {5-{\sqrt {3}}}{3}}}
3
(
5
+
3
)
22
{\displaystyle {\frac {3\left(5+{\sqrt {3}}\right)}{22}}}
[ 註 1]
^ Wolfram, Stephen . " (2*sqrt(6)/9)/(4*sqrt(2)/9)" Wolfram Alpha : Computational Knowledge Engine, Wolfram Research (英语) . ^ 來源給出的結果為長邊長為
4
2
9
{\displaystyle {\frac {4{\sqrt {2}}}{9}}}
2
6
9
{\displaystyle {\frac {2{\sqrt {6}}}{9}}}
[ 6]
2
6
9
:
4
2
9
{\displaystyle {\frac {2{\sqrt {6}}}{9}}:{\frac {4{\sqrt {2}}}{9}}}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
[ 註 3]
^ Lherbette, Michael and Redlingshöfer, Lisa and Brodsky, Frances M and Schaap, Iwan AT and Dannhauser, Philip N. The AP2 adaptor enhances clathrin coat stiffness . The FEBS journal (Wiley Online Library). 2019, 286 (20): 4074–4085 [2023-01-24 ] . (原始内容存档 于2023-01-24). ^ Morgan, Benjamin J. Mechanistic Origin of Superionic Lithium Diffusion in Anion-Disordered Li6PS5 X Argyrodites. Chemistry of Materials (ACS Publications). 2021, 33 (6): 2004–2018. ^ Johnson Solid Near Misses: Number 22 . [2013-03-07 ] . (原始内容存档 于2014-05-02). ^ 4.0 4.1 David I. McCooey. Truncated Catalan Solids: 6-Truncated Triakis Tetrahedron (canonical) . [2023-01-23 ] . (原始内容存档 于2023-01-24). ^ 5.0 5.1 5.2 David I. McCooey. Truncated Catalan Solids: 6-Truncated Triakis Tetrahedron (pentagon sides: 1 long, 4 short) . [2023-01-23 ] . (原始内容存档 于2023-01-24). ^ 6.0 6.1 6.2 David I. McCooey. Truncated Catalan Solids: 6-Truncated Triakis Tetrahedron (circumscribed) . [2023-01-23 ] . (原始内容存档 于2023-01-24). ^ Apolinar, E.S. Illustrated Glossary for School Mathematics . Efrain Soto Apolinar. 2023 [2023-01-24 ] . ISBN 9786072941311存档 于2023-01-17). ^ Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim. The Symmetries of Things. 2008: 332. ISBN 978-1568812205 ^ Grünbaum, B; Shephard, G. C. Tilings with Congruent Tiles . Bull. Amer. Math. Soc. 1980, 3 (3): 951–973 [2023-01-24 ] . doi:10.1090/s0273-0979-1980-14827-2 存档 于2016-03-03). ^ Richard Klitzing. hexakis truncated tetrahedron, hiktut . bendwavy.org. [2023-01-02 ] . (原始内容存档 于2023-01-24).