เกรเดียนต์

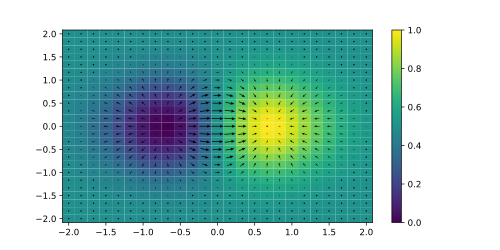
ในสองภาพข้างบนได้แสดงแทนฟังก์ชันสเกลาร์ด้วยสีดำและสีขาว สีดำแทนตำแหน่งที่ฟังก์ชันมีค่าสูงกว่า และเกรเดียนต์ที่แต่ละจุดแสดงโดยลูกศรสีฟ้า สังเกตว่าเกรเดียนต์ชี้ไปทิศทางที่ฟังก์ชันมีค่ามากขึ้น

ในแคลคูลัสเวกเตอร์ เกรเดียนต์ (อังกฤษ: gradient) คือการดำเนินการกับฟังก์ชันหลายตัวแปร ${\displaystyle f}$ ซึ่งหาอนุพันธ์ได้ซึ่งมีค่าเป็นสเกลาร์ ผลลัพธ์ที่ได้คือสนามเวกเตอร์ ${\displaystyle \nabla f}$ ที่ค่าที่แต่ละจุดจะชี้ไปในทิศทางที่ ${\displaystyle f}$ มีค่ามากขึ้นที่สุด[1] และขนาดของเวกเตอร์เท่ากับอัตราการเพิ่มขึ้นในทิศทางนั้น ๆ เรียกสนามเวกเตอร์นี้ว่า เกรเดียนต์ของ ${\displaystyle f}$สัญลักษณ์ ${\displaystyle \nabla }$ เรียกว่าสัญลักษณ์นาบลา (nabla) หรือ เดล (del)

เนื่องจากเกรเดียนต์ระบุทิศทางที่ฟังก์ชันมีค่าเพิ่มขึ้นมากที่สุด และทิศทางตรงกันข้ามของเกรเดียนต์ฟังก์ชันจะมีค่าน้อยที่สุด เกรเดียนต์จึงมีความสำคัญในวิชาการหาค่าเหมาะที่สุด เพื่อหาค่าที่น้อยที่สุดของฟังก์ชัน ${\displaystyle f}$ ด้วยขั้นตอนวิธีการเคลื่อนลงตามความชัน (gradient descent)

แนวคิดจูงใจของเกรเดียนต์

เกรเดียนต์ของฟังก์ชันสองมิติ f(x, y) = xe^−(x2 + y2) ถูกพล็อตโดยใช้ลูกศรเหนือค่าของฟังก์ชันซึ่งแสดงโดยใช้สี

พิจารณาห้องที่อุณหภูมิภายในกำหนดด้วยฟังก์ชันค่าสเกลาร์ ${\displaystyle T}$ นั่นคือที่จุด ${\displaystyle (x,y,z)}$ อุณหภูมิที่ตำแหน่งนั้นคือ ${\displaystyle T(x,y,z)}$ และเป็นอิสระจากเวลา

เกรเดียนต์ของ ${\displaystyle T}$ ที่จุด ${\displaystyle (x,y,z)}$ จะบอกทิศทางที่อุณหภูมิเพิ่มขึ้นเร็วที่สุดเมื่อเดินทางออกจากจุด ${\displaystyle (x,y,z)}$ และขนาดของเกรเดียนต์จะระบุอัตราเร็วที่อุณหภูมิเพิ่มขึ้นในทิศทางนั้น

พิจารณาพื้นผิวที่ความสูงจากระดับน้ำทะเลที่จุด ${\displaystyle (x,y)}$ กำหนดโดยฟังก์ชัน ${\displaystyle H(x,y)}$ เกรเดียนต์ของ ${\displaystyle H}$ ที่จุด ${\displaystyle (x,y)}$ จะเป็นเวกเตอร์ที่ชี้บอกทิศทางที่ชันมากที่สุดจากจุดนั้น และความชันจะเท่ากับขนาดของเวกเตอร์เกรเดียนต์

นอกจากนี้ เกรเดียนต์ยังสามารถใช้วัดอัตราการเปลี่ยนแปลงของฟังก์ชันค่าสเกลาร์ในทิศทางอื่นนอกเหนือไปจากทิศทางของเกรเดียนต์เอง โดยการหาผลคูณจุด สมมติว่าความชันสูงสุดที่จุด ๆ หนึ่งบนเนินเขาเท่ากับ 40% ถนนขึ้นเนินที่ทำมุมอื่น ๆ ย่อมจะมีความชันน้อยกว่า เราสามารถหาความชันได้โดยหาผลคูณจุดระหว่างเกรเดียนต์ที่จุดที่สนใจ และเวกเตอร์หน่วยที่ชี้ไปตามทิศทางของถนน

โดยทั่วไปกว่านั้น ถ้าฟังก์ชัน ${\displaystyle H}$ ที่ระบุความสูงของเนิน เป็นฟังก์ชันหาอนุพันธ์ได้ แล้วเกรเดียนต์ของ ${\displaystyle H}$ คูณสเกลาร์กับเวกเตอร์หน่วยจะเท่ากับความชันของเนินในทิศทางนั้น หรือก็คืออนุพันธ์ระบุทิศทางของ ${\displaystyle H}$ ในทิศทางของเวกเตอร์หน่วยนั้น

สัญลักษณ์ที่ใช้

เกรเดียนต์ของฟังก์ชัน ${\displaystyle f}$ ที่จุด ${\displaystyle a}$ นิยมเขียนแทนด้วย ${\displaystyle \nabla f(a)}$ แต่อาจจะมีสัญลักษณ์อื่น ๆ เช่น

• ${\displaystyle {\vec {\nabla }}f(a)}$ : เพื่อเจาะจงความเป็นเวกเตอร์ของเกรเดียนต์
• ${\displaystyle \operatorname {grad} f}$
• ${\displaystyle \partial _{i}f}$ and ${\displaystyle f_{i}}$ : โดยใช้สัญกรณ์ของไอน์ชไตน์ (Einstein notation) โดยดรรชนีที่ซ้ำให้ถือว่าถูกบวกอยู่ (i)

นิยาม

เกรเดียนต์ของฟังก์ชัน f(x,y) = −(cos^2x + cos^2y)^2 แสดงผ่านสนามเวกเตอร์ที่ถูกฉายลงบนระนาบด้านล่าง

เกรเดียนต์ ของฟังก์ชันสเกลาร์ ${\displaystyle f(x_{1},\dotsc ,x_{n})}$ เขียนแทนด้วย ${\displaystyle \nabla f}$ หรือ ${\displaystyle {\vec {\nabla }}f}$ นิยามให้เป็นสนามเวกเตอร์ซึ่งมีเพียงแบบเดียวที่ผลคูณจุดกับเวกเตอร์ ${\displaystyle \mathbf {v} }$ ที่จุด ${\displaystyle x}$ จะเท่ากับอนุพันธ์ระบุทิศทางของ ${\displaystyle f}$ ไปตาม ${\displaystyle \mathbf {v} }$[2] นั่นคือ $${\displaystyle {\big (}\nabla f(x){\big )}\cdot \mathbf {v} =D_{\mathbf {v} }f(x)}$$

เมื่อพจน์ทางขวามือคืออนุพันธ์ระบุทิศทางของฟังก์ชัน ${\displaystyle f}$ ในทางรูปนัยเราจะกล่าวว่าการหาอนุพันธ์เป็น ดูอัล ของเกรเดียนต์ มีวิธีการหาค่าของเกรเดียนต์หลายวิธีซึ่งเสนอไว้ด้านล่าง

สัญลักษณ์ ${\displaystyle \nabla }$ เรียกว่าตัวดำเนินการเชิงอนุพันธ์สำหรับเวกเตอร์

ขนาดและทิศทางของเกรเดียนต์ไม่ขึ้นกับระบบพิกัดที่ใช้[3][4]

ระบบพิกัดคาร์ทีเซียน

ในระบบพิกัดคาร์ทีเซียนสามมิติพร้อมกับเมตริกแบบยูคลิด เกรเดียนต์ถ้ามีค่าจะเป็นไปตามสมการ

$${\displaystyle \nabla f={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} +{\frac {\partial f}{\partial z}}\mathbf {k} }$$

เมื่อ i, j, k เป็นเวกเตอร์หนึ่งหน่วยมาตรฐานในทิศทางของระบบพิกัด x, y และ z ตามลำดับ ตัวอย่างเช่น เกรเดียนต์ของฟังก์ชัน $${\displaystyle f(x,y,z)=2x+3y^{2}-\sin(z)}$$ คือ $${\displaystyle \nabla f(x,y,z)=2\mathbf {i} +6y\mathbf {j} -\cos(z)\mathbf {k} }$$ หรือเขียนแทนด้วย$${\displaystyle \nabla f(x,y,z)={\begin{bmatrix}2\\6y\\-\cos z\end{bmatrix}}}$$

ในบางการใช้งานนิยมเขียนเกรเดียนต์เป็นเวกเตอร์แถวหรือเวกเตอร์หลัก

อ้างอิง

1. * Bachman (2007, p. 77)
   • Downing (2010, pp. 316–317)
   • Kreyszig (1972, p. 309)
   • McGraw-Hill (2007, p. 196)
   • Moise (1967, p. 684)
   • Protter & Morrey (1970, p. 715)
   • Swokowski et al. (1994, pp. 1036, 1038–1039)
2. Garling, D. J. H. (2013). A course in mathematical analysis. Cambridge: Cambridge University Press. p. 486. ISBN 978-1-107-03203-3.
3. Kreyszig (1972, pp. 308–309)
4. Stoker (1969, p. 292)

บรรณานุกรม

• Bachman, David (2007), Advanced Calculus Demystified, New York: McGraw-Hill, ISBN 978-0-07-148121-2
• Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Company, ISBN 0-395-14017-X
• Downing, Douglas, Ph.D. (2010), Barron's E-Z Calculus, New York: Barron's, ISBN 978-0-7641-4461-5
• Dubrovin, B. A.; Fomenko, A. T.; Novikov, S. P. (1991). Modern Geometry—Methods and Applications: Part I: The Geometry of Surfaces, Transformation Groups, and Fields. Graduate Texts in Mathematics (2nd ed.). Springer. ISBN 978-0-387-97663-1.
• Harper, Charlie (1976), Introduction to Mathematical Physics, New Jersey: Prentice-Hall, ISBN 0-13-487538-9
• Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3rd ed.), New York: Wiley, ISBN 0-471-50728-8
• "McGraw Hill Encyclopedia of Science & Technology". McGraw-Hill Encyclopedia of Science & Technology (10th ed.). New York: McGraw-Hill. 2007. ISBN 978-0-07-144143-8.
• Moise, Edwin E. (1967), Calculus: Complete, Reading: Addison-Wesley
• Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
• Schey, H. M. (1992). Div, Grad, Curl, and All That (2nd ed.). W. W. Norton. ISBN 0-393-96251-2. OCLC 25048561.
• Stoker, J. J. (1969), Differential Geometry, New York: Wiley, ISBN 0-471-82825-4
• Swokowski, Earl W.; Olinick, Michael; Pence, Dennis; Cole, Jeffery A. (1994), Calculus (6th ed.), Boston: PWS Publishing Company, ISBN 0-534-93624-5
• Arens, T.; Hettlich, F.; Karpfinger, C.; Kockelkorn, U.; Lichtenegger, K.; Stachel, H. (2022), Mathematik (5th ed.), Springer Spektrum Berlin, ISBN 978-3-662-64388-4