–Ę–ĺ—á–Ķ—á–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ
–Ę–ĺ—á–Ķ—á–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ ‚ÄĒ –≥—Ä—É–Ņ–Ņ–į –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ, –Ĺ–Ķ –Ņ–Ķ—Ä–Ķ–ľ–Ķ—Č–į—é—Č–į—Ź –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā, –ł–Ľ–ł –≥—Ä—É–Ņ–Ņ–į –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ —Ā—Ą–Ķ—Ä—č. –ď—Ä—É–Ņ–Ņ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–ĺ–Ļ –ĺ—Ä—ā–ĺ–≥–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č O(3), –≥—Ä—É–Ņ–Ņ—č –≤—Ā–Ķ—Ö –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ, –ĺ—Ā—ā–į–≤–Ľ—Ź—é—Č–ł—Ö –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –Ĺ–Ķ–Ņ–ĺ–ī–≤–ł–∂–Ĺ—č–ľ, –ł–Ľ–ł, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –≥—Ä—É–Ņ–Ņ—č –ĺ—Ä—ā–ĺ–≥–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č—Ö –ľ–į—ā—Ä–ł—Ü. O(3) —Ā–į–ľ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–ĺ–Ļ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č[–į–Ĺ–≥–Ľ.] E(3) –ī–≤–ł–∂–Ķ–Ĺ–ł–Ļ 3-–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į. –ď—Ä—É–Ņ–Ņ—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ĺ–Ī—ä–Ķ–ļ—ā–ĺ–≤ —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–į–ľ–ł –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł. –°–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –į–Ĺ–į–Ľ–ł–∑ –≥—Ä—É–Ņ–Ņ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –į–Ĺ–į–Ľ–ł–∑–ĺ–ľ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č—Ö —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ. –í—Ā–Ķ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ –ĺ–Ī—ä–Ķ–ļ—ā–į –ł–ľ–Ķ—é—ā –ĺ–ī–Ĺ—É –ł–Ľ–ł –Ī–ĺ–Ľ–Ķ–Ķ —Ą–ł–ļ—Ā–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ (–Ĺ–Ķ –ľ–Ķ–Ĺ—Ź—é—Č–ł—Ö –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ł —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł). –ú—č –≤—č–Ī–ł—Ä–į–Ķ–ľ –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –ĺ–ī–Ĺ–ĺ–Ļ –ł–∑ —ā–į–ļ–ł—Ö —ā–ĺ—á–Ķ–ļ. –ď—Ä—É–Ņ–Ņ–į —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ –ĺ–Ī—ä–Ķ–ļ—ā–į –ł–Ĺ–ĺ–≥–ī–į –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ļ–į–ļ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –Ķ–≥–ĺ –≥—Ä—É–Ņ–Ņ–Ķ –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –ł–Ľ–ł —Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–Ķ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł, –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—é –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ł –≥—Ä—É–Ņ–Ņ—č –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ SO(3) —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į. –ď—Ä—É–Ņ–Ņ–į –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –ĺ–Ī—ä–Ķ–ļ—ā–į —Ā–ĺ–≤–Ņ–į–ī–į–Ķ—ā —Ā –Ķ–≥–ĺ –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —ā–ĺ–≥–ī–į –ł —ā–ĺ–Ľ—Ć–ļ–ĺ —ā–ĺ–≥–ī–į, –ļ–ĺ–≥–ī–į –ĺ–Ī—ä–Ķ–ļ—ā —Ö–ł—Ä–į–Ľ–Ķ–Ĺ. –Ę–ĺ—á–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ –ł–Ĺ—ā–Ķ–Ĺ—Ā–ł–≤–Ĺ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā—Ā—Ź –≤ —Ö–ł–ľ–ł–ł, –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–Ĺ–ĺ –Ņ—Ä–ł –ĺ–Ņ–ł—Ā–į–Ĺ–ł–ł —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ –ľ–ĺ–Ľ–Ķ–ļ—É–Ľ—č –ł –ľ–ĺ–Ľ–Ķ–ļ—É–Ľ—Ź—Ä–Ĺ—č—Ö –ĺ—Ä–Ī–ł—ā–į–Ľ–Ķ–Ļ, –ĺ–Ī—Ä–į–∑—É—é—Č–ł—Ö –ļ–ĺ–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ—č–Ķ —Ā–≤—Ź–∑–ł, –ł –≤ —ć—ā–ĺ–ľ –ļ–ĺ–Ĺ—ā–Ķ–ļ—Ā—ā–Ķ —ć—ā–ł –≥—Ä—É–Ņ–Ņ—č –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź –ľ–ĺ–Ľ–Ķ–ļ—É–Ľ—Ź—Ä–Ĺ—č–ľ–ł —ā–ĺ—á–Ķ—á–Ĺ—č–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł[–į–Ĺ–≥–Ľ.]. –ö–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–ľ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ–ľ —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ, –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–ľ –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ—č—Ö –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–Ķ–Ļ, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—Č–ł—Ö—Ā—Ź –≤ –ĺ–ī–Ĺ–ĺ–Ļ —ā–ĺ—á–ļ–Ķ. –ď—Ä—É–Ņ–Ņ–į –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į —Ä–į–Ĺ–≥–į n –ł–ľ–Ķ–Ķ—ā n –∑–Ķ—Ä–ļ–į–Ľ –ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī–ł–į–≥—Ä–į–ľ–ľ–ĺ–Ļ –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į ‚ÄĒ –Ē—č–Ĺ–ļ–ł–Ĺ–į. –Ě–ĺ—ā–į—Ü–ł—Ź –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į[–į–Ĺ–≥–Ľ.] –Ņ—Ä–Ķ–ī–ĺ—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ļ–ĺ–Ī–ĺ—á–Ĺ—É—é –∑–į–Ņ–ł—Ā—Ć, —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ—É—é –ī–ł–į–≥—Ä–į–ľ–ľ–Ķ –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į —Ā —Ā–ł–ľ–≤–ĺ–Ľ–į–ľ–ł —Ä–į–∑–ľ–Ķ—ā–ļ–ł –ī–Ľ—Ź –≤—Ä–į—Č–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –ł –ī—Ä—É–≥–ł—Ö —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ. –°—ā—Ä—É–ļ—ā—É—Ä–į –≥—Ä—É–Ņ–Ņ—čSO(3) —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–ĺ–Ļ E+(3)[–į–Ĺ–≥–Ľ.], –ļ–ĺ—ā–ĺ—Ä–į—Ź —Ā–ĺ—Ā—ā–ĺ–ł—ā –ł–∑ –Ņ—Ä—Ź–ľ—č—Ö –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ, —ā.–Ķ. –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ, —Ā–ĺ—Ö—Ä–į–Ĺ—Ź—é—Č–ł—Ö –ĺ—Ä–ł–Ķ–Ĺ—ā–į—Ü–ł—é. –ě–Ĺ–į —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł —ć—ā–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č, –ĺ—Ā—ā–į–≤–Ľ—Ź—é—Č–ł–Ķ –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –Ī–Ķ–∑ –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź. O(3) —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ—Ä—Ź–ľ—č–ľ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ–ľ SO(3) –ł –≥—Ä—É–Ņ–Ņ—č, –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ:
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ł–ľ–Ķ–Ķ—ā—Ā—Ź 1-–≤-1 —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ľ–Ķ–∂–ī—É –≤—Ā–Ķ–ľ–ł –Ņ—Ä—Ź–ľ—č–ľ–ł –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł—Ź–ľ–ł –ł –Ĺ–Ķ–Ņ—Ä—Ź–ľ—č–ľ–ł –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł—Ź–ľ–ł, –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ—č–ľ–ł —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ. –ė–ľ–Ķ–Ķ—ā—Ā—Ź —ā–į–ļ–∂–Ķ 1-–≤-1 —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ľ–Ķ–∂–ī—É –≤—Ā–Ķ–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł –Ņ—Ä—Ź–ľ—č—Ö –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ H –≤ O(3) –ł –≤—Ā–Ķ–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł K –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ –≤ O(3), —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–ł—Ö —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ—É—é –ł–Ĺ–≤–Ķ—Ä—Ā–ł—é:
–Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ķ—Ā–Ľ–ł H —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–ĺ–Ļ C2, —ā–ĺ K —Ä–į–≤–Ĺ–ĺ C2h. –ē—Ā–Ľ–ł –∂–Ķ H —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–ĺ–Ļ C3, —ā–ĺ K —Ä–į–≤–Ĺ–ĺ S6. (–°–ľ–ĺ—ā—Ä–ł—ā–Ķ –Ĺ–ł–∂–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —ć—ā–ł—Ö –≥—Ä—É–Ņ–Ņ.) –ē—Ā–Ľ–ł –≥—Ä—É–Ņ–Ņ–į –Ņ—Ä—Ź–ľ—č—Ö –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ H –ł–ľ–Ķ–Ķ—ā –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ—É L —Ā –ł–Ĺ–ī–Ķ–ļ—Ā–ĺ–ľ 2, —ā–ĺ, –ļ—Ä–ĺ–ľ–Ķ –≥—Ä—É–Ņ–Ņ—č, —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–Ķ–Ļ —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ—É—é —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é, –Ķ—Ā—ā—Ć –Ķ—Č—Ď —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–į—Ź –≥—Ä—É–Ņ–Ņ–į, —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–į—Ź –Ĺ–Ķ–Ņ—Ä—Ź–ľ—č–Ķ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł, –Ĺ–ĺ –Ĺ–Ķ —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–ł–Ķ —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł:
–≥–ī–Ķ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł—Ź ( A, I ) –ĺ—ā–ĺ–∂–ī–Ķ—Ā—ā–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ā A. –ü—Ä–ł–ľ–Ķ—Ä–ĺ–ľ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć C4 –ī–Ľ—Ź H –ł S4 –ī–Ľ—Ź M. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, M –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź –ł–∑ H —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ –ł–∑ H \ L. –≠—ā–į –≥—Ä—É–Ņ–Ņ–į M —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ, –ł–∑–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ–Ļ H. –ě–Ī—Ä–į—ā–Ĺ–ĺ, –ī–Ľ—Ź –≤—Ā–Ķ—Ö –≥—Ä—É–Ņ–Ņ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł, —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–ł—Ö –Ĺ–Ķ–Ņ—Ä—Ź–ľ—č–Ķ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł, –Ĺ–ĺ –Ĺ–Ķ —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–ł–Ķ —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł, –ľ—č –ľ–ĺ–∂–Ķ–ľ –Ņ–ĺ–Ľ—É—á–ł—ā—Ć –≥—Ä—É–Ņ–Ņ—É –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –Ņ—É—ā—Ď–ľ –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ļ –Ĺ–Ķ–Ņ—Ä—Ź–ľ—č–ľ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł—Ź–ľ. –í –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ —Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–į—Ź –≥—Ä—É–Ņ–Ņ–į –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –Ņ–ĺ—Ä—Ź–ī–ļ–į k Ck (–≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –Ĺ–į —É–≥–ĺ–Ľ 180¬į/ k) –ī–Ľ—Ź –Ľ—é–Ī—č—Ö –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —Ü–Ķ–Ľ—č—Ö k —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–ĺ–Ļ O(2,R) –ł SO(2,R). –°–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–Ļ –ĺ—Ā–ł —Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–į—Ź –≥—Ä—É–Ņ–Ņ–į –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –Ņ–ĺ—Ä—Ź–ī–ļ–į k –≤–ĺ–ļ—Ä—É–≥ –ĺ—Ā–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–ĺ–Ļ –≤—Ā–Ķ—Ö –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –≤–ĺ–ļ—Ä—É–≥ –ĺ—Ā–ł. –ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –Ľ—é–Ī–į—Ź –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–į —Ā –ł–Ĺ–ī–Ķ–ļ—Ā–ĺ–ľ –ī–≤–į –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–į, –≥—Ä—É–Ņ–Ņ–į –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ (Cn) —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ –ļ–į–ļ –≤ –≥—Ä—É–Ņ–Ņ–Ķ, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–Ļ –ī–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–ł–Ķ–ľ –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ—č—Ö —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–Ķ–Ļ, —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–ł—Ö –ĺ—Ā–ł (Cnv), —ā–į–ļ –ł –≤ –≥—Ä—É–Ņ–Ņ–Ķ, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–Ļ –ī–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–ł–Ķ–ľ –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ—č—Ö —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–Ķ–Ļ, –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č—Ö –ĺ—Ā—Ź–ľ (Cnh). –Ę—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ—č–Ķ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł, –ĺ—Ā—ā–į–≤–Ľ—Ź—é—Č–ł–Ķ –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –Ĺ–Ķ–Ņ–ĺ–ī–≤–ł–∂–Ĺ—č–ľ–ė–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į R3, –ĺ—Ā—ā–į–≤–Ľ—Ź—é—Č–ł–Ķ –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –Ĺ–Ķ–Ņ–ĺ–ī–≤–ł–∂–Ĺ—č–ľ –ł –ĺ–Ī—Ä–į–∑—É—é—Č–ł–Ķ –≥—Ä—É–Ņ–Ņ—É O(3,R), –ľ–ĺ–∂–Ĺ–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć –Ĺ–į –≥—Ä—É–Ņ–Ņ—č —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
4-—Ź –ł 5-—Ź –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł, –≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, –į –≤ –Ī–ĺ–Ľ–Ķ–Ķ —ą–ł—Ä–ĺ–ļ–ĺ–ľ —Ā–ľ—č—Ā–Ľ–Ķ –ł 6-—Ź, –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź –Ĺ–Ķ—Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–ľ–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź–ľ–ł[–į–Ĺ–≥–Ľ.]. –°–ĺ–Ņ—Ä—Ź–∂—Ď–Ĺ–Ĺ–ĺ—Ā—ā—Ć–ē—Ā–Ľ–ł —Ā—Ä–į–≤–Ĺ–ł–≤–į—é—ā—Ā—Ź —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ī–≤—É—Ö –ĺ–Ī—ä–Ķ–ļ—ā–ĺ–≤, —ā–ĺ –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –ī–Ľ—Ź –ļ–į–∂–ī–ĺ–≥–ĺ –ĺ–Ī—ä–Ķ–ļ—ā–į –≤—č–Ī–ł—Ä–į–Ķ—ā—Ā—Ź –ĺ—ā–ī–Ķ–Ľ—Ć–Ĺ–ĺ, —ā.–Ķ. –ĺ–Ĺ–ł –Ĺ–Ķ –ĺ–Ī—Ź–∑–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ī—É–ī—É—ā –ł–ľ–Ķ–Ķ—ā –ĺ–ī–ł–Ĺ –ł —ā–ĺ—ā –∂–Ķ —Ü–Ķ–Ĺ—ā—Ä. –Ď–ĺ–Ľ–Ķ–Ķ —ā–ĺ–≥–ĺ, —Ā—á–ł—ā–į–Ķ—ā—Ā—Ź, —á—ā–ĺ –ĺ–Ī—ä–Ķ–ļ—ā—č –ł–ľ–Ķ—é—ā —ā–ĺ—ā –∂–Ķ —ā–ł–Ņ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł, –Ķ—Ā–Ľ–ł –ł—Ö –≥—Ä—É–Ņ–Ņ—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ā–ĺ–Ņ—Ä—Ź–∂—Ď–Ĺ–Ĺ—č–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł –≥—Ä—É–Ņ–Ņ—č O(3) (–ī–≤–Ķ –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ—č H1 –ł H2 –≥—Ä—É–Ņ–Ņ—č G —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ—č, –Ķ—Ā–Ľ–ł —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā g ‚ąą G, —ā–į–ļ–ĺ–Ļ, —á—ā–ĺ H1 = g‚ąí1H2g ). –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ī–≤–į —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ—č—Ö –ĺ–Ī—ä–Ķ–ļ—ā–į –ł–ľ–Ķ—é—ā —ā–ĺ—ā –∂–Ķ —ā–ł–Ņ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł, –Ķ—Ā–Ľ–ł
–í —Ā–Ľ—É—á–į–Ķ–ľ –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ł—Ö –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–Ķ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ł/–ł–Ľ–ł –ĺ—Ā–Ķ–Ļ –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –ī–≤–Ķ –≥—Ä—É–Ņ–Ņ—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ł–ľ–Ķ—é—ā —ā–ĺ—ā –∂–Ķ —ā–ł–Ņ —ā–ĺ–≥–ī–į, –ł —ā–ĺ–Ľ—Ć–ļ–ĺ —ā–ĺ–≥–ī–į, –ļ–ĺ–≥–ī–į –ł–ľ–Ķ–Ķ—ā—Ā—Ź –≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ, –ĺ—ā–ĺ–Ī—Ä–į–∂–į—é—Č–Ķ–Ķ –Ņ–ĺ–Ľ–Ĺ—É—é —Ā—ā—Ä—É–ļ—ā—É—Ä—É –Ņ–Ķ—Ä–≤–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –≤–ĺ –≤—ā–ĺ—Ä—É—é. (–§–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł, –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ī–ĺ–Ľ–Ķ–Ķ —á–Ķ–ľ –ĺ–ī–Ĺ–ĺ –≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ, –Ĺ–ĺ –Ĺ–Ķ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ). –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā —ā–į–ļ–∂–Ķ –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ–ĺ–Ķ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł–Ķ —Ā—ā—Ä—É–ļ—ā—É—Ä—č, –Ĺ–ĺ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā–ł –≤ —ć—ā–ĺ–ľ –Ĺ–Ķ—ā, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —Ā—ā—Ä—É–ļ—ā—É—Ä–į —Ā–į–ľ–į –Ņ–ĺ —Ā–Ķ–Ī–Ķ –į—Ö–ł—Ä–į–Ľ—Ć–Ĺ–į. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ķ—Ā–Ľ–ł –≥—Ä—É–Ņ–Ņ–į —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā –ĺ—Ā—Ć –Ņ–ĺ—Ä—Ź–ī–ļ–į 3, –ĺ–Ĺ–į —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –≤ –ī–≤—É—Ö –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ—č—Ö –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź—Ö (—Ā—ā—Ä—É–ļ—ā—É—Ä–į —Ö–ł—Ä–į–Ľ—Ć–Ĺ–į –ī–Ľ—Ź 11 –Ņ–į—Ä –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł—Ö –≥—Ä—É–Ņ–Ņ —Ā –≤–ł–Ĺ—ā–ĺ–≤–ĺ–Ļ –ĺ—Ā—Ć—é). –Ď–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł–°—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, "—Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–į—Ź –≥—Ä—É–Ņ–Ņ–į" (–Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–į–≥–į–Ķ—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–į, –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–Ĺ–į—Ź –ĺ–ī–Ĺ–ł–ľ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–ľ ‚Äď –Ĺ–Ķ –Ņ—É—ā–į—ā—Ć —Ā –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —Ā –ļ—Ä—É—á–Ķ–Ĺ–ł–Ķ–ľ), –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–Ĺ–į—Ź –≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ–ľ –Ĺ–į –ł—Ä—Ä–į—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č–Ļ —É–≥–ĺ–Ľ –≤–ĺ–ļ—Ä—É–≥ –ĺ—Ā–ł. –ú—č –ľ–ĺ–∂–Ķ–ľ —Ā–ĺ–∑–ī–į—ā—Ć –Ĺ–Ķ—Ü–ł–ļ–Ľ–ł—á–Ĺ—č–Ķ –į–Ī–Ķ–Ľ–Ķ–≤—č –≥—Ä—É–Ņ–Ņ—č –Ņ—É—ā—Ď–ľ –ī–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–ł—Ź –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –ļ—Ä—É—á–Ķ–Ĺ–ł–Ļ –≤–ĺ–ļ—Ä—É–≥ —ā–ĺ–Ļ –∂–Ķ –ĺ—Ā–ł. –°—É—Č–Ķ—Ā—ā–≤—É—é—ā —ā–į–ļ–∂–Ķ –Ĺ–Ķ–į–Ī–Ķ–Ľ–Ķ–≤—č –≥—Ä—É–Ņ–Ņ—č, –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–Ĺ—č–Ķ –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź–ľ–ł –≤–ĺ–ļ—Ä—É–≥ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö –ĺ—Ā–Ķ–Ļ. –ě–Ĺ–ł –ĺ–Ī—č—á–Ĺ–ĺ (–≤ –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ) —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ā–≤–ĺ–Ī–ĺ–ī–Ĺ—č–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł. –ě–Ĺ–ł –Ī—É–ī—É—ā –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–ľ–ł, –Ķ—Ā–Ľ–ł –Ĺ–Ķ –≤—č–Ī—Ä–į—ā—Ć –≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ. –í—Ā–Ķ —É–Ņ–ĺ–ľ—Ź–Ĺ—É—ā—č–Ķ –ī–ĺ —ć—ā–ĺ–≥–ĺ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –Ĺ–Ķ —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –∑–į–ľ–ļ–Ĺ—É—ā—č–ľ–ł –ļ–į–ļ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł–Ķ –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ—č –≥—Ä—É–Ņ–Ņ—č O(3).  –ü–ĺ–Ľ–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į O(3) —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł. SO(3) —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–Ķ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ. –Ē—Ä—É–≥–ł–Ķ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł —Ā–ĺ—Ā—ā–ĺ—Ź—ā –ł–∑ –≤—Ā–Ķ—Ö –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –≤–ĺ–ļ—Ä—É–≥ –ĺ—Ā–ł, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā, –ł –ł–∑ —ā–į–ļ–ĺ–≥–ĺ –∂–Ķ –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź —Ā –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–Ķ–Ļ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–ł—Ö —á–Ķ—Ä–Ķ–∑ —ć—ā—É –ĺ—Ā—Ć –ł/–ł–Ľ–ł –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –ł –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–ĺ–Ļ –ĺ—Ā–ł. –≠—ā–ł –≥—Ä—É–Ņ–Ņ—č —Ā –∑–Ķ—Ä–ļ–į–Ľ–į–ľ–ł, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–ł–ľ–ł —á–Ķ—Ä–Ķ–∑ –ĺ—Ā—Ć, —Ā –ł–Ľ–ł –Ī–Ķ–∑ –∑–Ķ—Ä–ļ–į–Ľ–į, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–≥–ĺ —á–Ķ—Ä–Ķ–∑ –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –ł –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–ĺ–≥–ĺ –ĺ—Ā–ł, —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–į–ľ–ł —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ī–Ľ—Ź –ī–≤—É—Ö —ā–ł–Ņ–ĺ–≤ —Ü–ł–Ľ–ł–Ĺ–ī—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł[–į–Ĺ–≥–Ľ.]. –ě—ā–ľ–Ķ—ā–ł–ľ, —á—ā–ĺ –Ľ—é–Ī–ĺ–Ļ —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ –ĺ–Ī—ä–Ķ–ļ—ā, –ł–ľ–Ķ—é—Č–ł–Ļ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ –≤—Ä–į—Č–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł, –Ī—É–ī–Ķ—ā —ā–į–ļ–∂–Ķ –ł–ľ–Ķ—ā—Ć –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ—č–Ķ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–Ķ–Ļ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–ł—Ö —á–Ķ—Ä–Ķ–∑ –ĺ—Ā—Ć. –ö–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł–°–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –≤ 3-–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ, –ĺ—Ā—ā–į–≤–Ľ—Ź—é—Č–ł–Ķ –Ĺ–į –ľ–Ķ—Ā—ā–Ķ –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā, –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—ā—Ā—Ź —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź–ľ–ł –Ĺ–į —Ā—Ą–Ķ—Ä–Ķ —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ –Ĺ–į—á–į–Ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā. –Ē–Ľ—Ź –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ—č—Ö —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ —Ā–ľ. —ā–į–ļ–∂–Ķ –ď—Ä—É–Ņ–Ņ—č —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł. –° —ā–ĺ—á–Ĺ–ĺ—Ā—ā—Ć—é –ī–ĺ —Ā–ĺ–Ņ—Ä—Ź–∂—Ď–Ĺ–Ĺ–ĺ—Ā—ā–ł –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ—č—Ö —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ —Ā–ĺ—Ā—ā–ĺ–ł—ā –ł–∑:
–Ě–į–Ī–ĺ—Ä —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ —Ā—Ö–ĺ–ī–Ķ–Ĺ —Ā –ī–ł—Ā–ļ—Ä–Ķ—ā–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ –Ņ–Ķ—Ä–Ķ–Ĺ–ĺ—Ā–į ‚ÄĒ 27 –ł–∑ 7 –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö —Ā–Ķ—Ä–ł–Ļ –ł 5 –ł–∑ 7 –ĺ—Ā—ā–į–≤—ą–ł—Ö—Ā—Ź, –≤—Ā–Ķ–≥–ĺ 32 —ā–į–ļ –Ĺ–į–∑—č–≤–į–Ķ–ľ—č—Ö –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ł—á–Ķ—Ā–ļ–ł—Ö —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ. –°–ľ. —ā–į–ļ–∂–Ķ –Ę–Ķ–ĺ—Ä–Ķ–ľ–į –ĺ –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł—Ö –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł—Ź—Ö[–į–Ĺ–≥–Ľ.]. –°–Ķ–ľ—Ć –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö —Ā–Ķ—Ä–ł–Ļ –≥—Ä—É–Ņ–Ņ –ĺ—Ā–Ķ–≤–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł–Ď–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ —Ā–Ķ—Ä–ł–ł –Ņ—Ä–ł–∑–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł—Ö –≥—Ä—É–Ņ–Ņ –ł–ľ–Ķ—é—ā –ł–Ĺ–ī–Ķ–ļ—Ā n, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ľ—é–Ī—č–ľ –Ĺ–į—ā—É—Ä–į–Ľ—Ć–Ĺ—č–ľ —á–ł—Ā–Ľ–ĺ–ľ. –í –ļ–į–∂–ī–ĺ–Ļ —Ā–Ķ—Ä–ł–ł n-—Ź –≥—Ä—É–Ņ–Ņ–į —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā –≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ –Ņ–ĺ—Ä—Ź–ī–ļ–į n –≤–ĺ–ļ—Ä—É–≥ –ĺ—Ā–ł, —ā.–Ķ. –≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ –Ĺ–į —É–≥–ĺ–Ľ 360¬į/n. –°–Ľ—É—á–į–Ļ n=1 —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É–Ķ—ā –ĺ—ā—Ā—É—ā—Ā—ā–≤–ł—é –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź. –°—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā —á–Ķ—ā—č—Ä–Ķ —Ā–Ķ—Ä–ł–ł –Ī–Ķ–∑ –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –ĺ—Ā–Ķ–Ļ –≤—Ä–į—Č–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł (—Ā–ľ. —Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł[–į–Ĺ–≥–Ľ.]) –ł —ā—Ä–ł —Ā –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł –ĺ—Ā—Ź–ľ–ł —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –Ņ–ĺ—Ä—Ź–ī–ļ–į 2 (—Ā–ľ. –ī–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ–į—Ź —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź). –ė—Ö –ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ–Ĺ–ł–ľ–į—ā—Ć –ļ–į–ļ —ā–ĺ—á–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –≤ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł[–į–Ĺ–≥–Ľ.], —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–Ĺ—č–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ—č–ľ–ł –ĺ—Ā—Ź–ľ–ł –ł –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź–ľ–ł –≤ –Ĺ–ł—Ö. –ě–Ĺ–ł —Ā–≤—Ź–∑–į–Ĺ—č —Ā –≥—Ä—É–Ņ–Ņ–į–ľ–ł –Ī–ĺ—Ä–ī—é—Ä–į [1] –ł –ľ–ĺ–≥—É—ā —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć—Ā—Ź –ļ–į–ļ –Ī–ĺ—Ä–ī—é—Ä–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č, –Ņ–ĺ–≤—ā–ĺ—Ä—Ź—é—Č–ł–Ķ—Ā—Ź n —Ä–į–∑ –≤–ĺ–ļ—Ä—É–≥ —Ü–ł–Ľ–ł–Ĺ–ī—Ä–į. –í —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ —ā–į–Ī–Ľ–ł—Ü–Ķ –ī–į–Ĺ—č –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ –≤–ł–ī—č –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ –ī–Ľ—Ź —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ: —Ā–ł–ľ–≤–ĺ–Ľ–ł–ļ–į –ď–Ķ—Ä–ľ–į–Ĺ–į ‚ÄĒ –ú–ĺ–≥–Ķ–Ĺ–į (–ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –≤ –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł–ł), —Ā–ł–ľ–≤–ĺ–Ľ—č –®—Ď–Ĺ—Ą–Ľ–ł—Ā–į (–ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –ī–Ľ—Ź –ĺ–Ņ–ł—Ā–į–Ĺ–ł—Ź –ľ–ĺ–Ľ–Ķ–ļ—É–Ľ—Ź—Ä–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł), –ĺ—Ä–Ī–ł—Ą–ĺ–Ľ–ī–Ĺ–į—Ź –Ĺ–ĺ—ā–į—Ü–ł—Ź[–į–Ĺ–≥–Ľ.] –ł –Ĺ–ĺ—ā–į—Ü–ł—Ź –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į[–į–Ĺ–≥–Ľ.]. –ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł–Ķ —ā—Ä–ł –Ĺ–Ķ —ā–ĺ–Ľ—Ć–ļ–ĺ —É–ī–ĺ–Ī–Ĺ—č –ī–Ľ—Ź –Ņ–ĺ–Ĺ–ł–ľ–į–Ĺ–ł—Ź —Ā–≤–ĺ–Ļ—Ā—ā–≤ —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ, –Ĺ–ĺ —ā–į–ļ–∂–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—ā –Ņ–ĺ—Ä—Ź–ī–ĺ–ļ –≥—Ä—É–Ņ–Ņ—č. –≠—ā–ĺ —É–Ĺ–ł—Ą–ł—Ü–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č–Ķ –∑–į–Ņ–ł—Ā–ł, –Ņ—Ä–ł–ľ–Ķ–Ĺ–ł–ľ—č–Ķ –ļ –≥—Ä—É–Ņ–Ņ–į–ľ –ĺ–Ī–ĺ–Ķ–≤ –ł –≥—Ä—É–Ņ–Ņ–į–ľ –Ī–ĺ—Ä–ī—é—Ä–ĺ–≤. –Ē–Ľ—Ź –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł—Ö –≥—Ä—É–Ņ–Ņ n –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź–ľ–ł 1, 2, 3, 4 –ł 6. –ē—Ā–Ľ–ł —É–ī–į–Ľ–ł—ā—Ć –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ķ –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł—Ź, –Ņ–ĺ–Ľ—É—á–ł–ľ –≥—Ä—É–Ņ–Ņ—č –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –Ĺ–į—ā—É—Ä–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —á–ł—Ā–Ľ–į. –°–Ķ—Ä–ł–ł:
–Ē–Ľ—Ź –Ĺ–Ķ—á—Ď—ā–Ĺ—č—Ö n –ľ—č –ł–ľ–Ķ–Ķ–ľ Z2n = Zn √ó Z2 –ł Dih2n = Dihn √ó Z2. –ü–ĺ–Ĺ—Ź—ā–ł–Ķ –≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ—Ć–Ĺ–į—Ź (h) –ł –≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ–į—Ź (v), –į —ā–į–ļ–∂–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ķ (–Ĺ–ł–∂–Ĺ–ł–Ķ) –ł–Ĺ–ī–Ķ–ļ—Ā—č, –ĺ—ā–Ĺ–ĺ—Ā—Ź—ā—Ā—Ź –ļ –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ—č–ľ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ź–ľ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č –ĺ—Ā–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź (–≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ—č) –ł–Ľ–ł –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č –ĺ—Ā–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź (–≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ—Ć–Ĺ—č). –ü—Ä–ĺ—Ā—ā–Ķ–Ļ—ą–ł–Ķ –Ĺ–Ķ—ā—Ä–ł–≤–ł–į–Ľ—Ć–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –ł–ľ–Ķ—é—ā –ł–Ĺ–≤–ĺ–Ľ—é—Ü–ł–ĺ–Ĺ–Ĺ—É—é —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é (–į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į Z2):
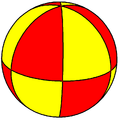
 –í—ā–ĺ—Ä–į—Ź –ł–∑ —ć—ā–ł—Ö –≥—Ä—É–Ņ–Ņ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–Ķ—Ä–≤–ĺ–Ļ –ł–∑ –≥—Ä—É–Ņ–Ņ —Ā –ĺ–ī–Ĺ–ĺ–Ļ –ĺ—Ā—Ć—é (—Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–ł—Ö –≥—Ä—É–Ņ–Ņ) Cn –Ņ–ĺ—Ä—Ź–ī–ļ–į n (–Ņ—Ä–ł–ľ–Ķ–Ĺ–ł–ľ—č—Ö —ā–į–ļ–∂–Ķ –ł –≤ –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ), –ļ–ĺ—ā–ĺ—Ä—č–Ķ –Ņ–ĺ—Ä–ĺ–∂–ī–į—é—ā—Ā—Ź –ĺ–ī–Ĺ–ł–ľ –≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ–ľ –Ĺ–į —É–≥–ĺ–Ľ 360¬į/n. –í –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ –ľ–ĺ–∂–Ĺ–ĺ –ī–ĺ–Ī–į–≤–ł—ā—Ć –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ—É—é –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ć, –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—É—é –ĺ—Ā–ł, —á—ā–ĺ –ī–į—Ď—ā –≥—Ä—É–Ņ–Ņ—É Cnh –Ņ–ĺ—Ä—Ź–ī–ļ–į 2n, –ł–Ľ–ł –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ n –∑–Ķ—Ä–ļ–į–Ľ, —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–ł—Ö –ĺ—Ā—Ć, —á—ā–ĺ –ī–į—Ď—ā –≥—Ä—É–Ņ–Ņ—É Cnv, —ā–į–ļ–∂–Ķ –Ņ–ĺ—Ä—Ź–ī–ļ–į 2n. –ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ—Ź—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ–ł—Ä–į–ľ–ł–ī—č —Ā n —Ā—ā–ĺ—Ä–ĺ–Ĺ–į–ľ–ł. –Ę–ł–Ņ–ł—á–Ĺ—č–Ļ –ĺ–Ī—ä–Ķ–ļ—ā —Ā –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł Cn –ł–Ľ–ł Dn ‚ÄĒ –Ņ—Ä–ĺ–Ņ–Ķ–Ľ–Ľ–Ķ—Ä. –ē—Ā–Ľ–ł –ī–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ—č –ł –≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ—č–Ķ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź, –ł –≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ—Ć–Ĺ—č–Ķ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł, –ł—Ö –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –ī–į—é—ā n –ĺ—Ā–Ķ–Ļ –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –Ĺ–į 180¬į, —ā–į–ļ —á—ā–ĺ –≥—Ä—É–Ņ–Ņ–į –Ī–ĺ–Ľ—Ć—ą–Ķ –Ĺ–Ķ –ĺ–ī–Ĺ–ĺ–ĺ—Ā–Ĺ–į—Ź. –≠—ā–į –Ĺ–ĺ–≤–į—Ź –≥—Ä—É–Ņ–Ņ–į –Ņ–ĺ—Ä—Ź–ī–ļ–į 4n –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź Dnh. –ē—Ď –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ—č –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ ‚ÄĒ –ī–ł—ć–ī—Ä–ł—á–Ķ—Ā–ļ–į—Ź –≥—Ä—É–Ņ–Ņ–į Dn –Ņ–ĺ—Ä—Ź–ī–ļ–į 2n, –ļ–ĺ—ā–ĺ—Ä–į—Ź, –≤—Ā—Ď –∂–Ķ, –ł–ľ–Ķ–Ķ—ā –ĺ—Ā–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –Ņ–ĺ—Ä—Ź–ī–ļ–į 2, –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č–Ķ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ–Ļ –ĺ—Ā–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź, –Ĺ–ĺ –Ĺ–Ķ –ł–ľ–Ķ–Ķ—ā –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–Ķ–Ļ –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź. –ó–į–ľ–Ķ—ā–ł–ľ, —á—ā–ĺ –≤ 2D Dn –≤–ļ–Ľ—é—á–į–Ķ—ā –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ľ–ĺ–∂–Ĺ–ĺ –≤–ł–ī–Ķ—ā—Ć –ļ–į–ļ –Ņ–Ķ—Ä–Ķ–ļ–ł–ī—č–≤–į–Ĺ–ł–Ķ —á–Ķ—Ä–Ķ–∑ –Ņ–Ľ–ĺ—Ā–ļ–ł–Ķ –ĺ–Ī—ä–Ķ–ļ—ā—č –Ī–Ķ–∑ —Ä–į–∑–Ľ–ł—á–Ķ–Ĺ–ł—Ź –Ľ–ł—Ü–Ķ–≤–ĺ–Ļ –ł –ĺ–Ī—Ä–į—ā–Ĺ–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ, –Ĺ–ĺ –≤ 3D –ī–≤–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —Ä–į–∑–Ľ–ł—á–į—é—ā—Ā—Ź ‚ÄĒ –≥—Ä—É–Ņ–Ņ–į —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā ¬ę–Ņ–Ķ—Ä–Ķ–ļ–ł–ī—č–≤–į–Ĺ–ł–Ķ —á–Ķ—Ä–Ķ–∑¬Ľ, –Ĺ–ĺ –Ĺ–Ķ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź. –ė–ľ–Ķ–Ķ—ā—Ā—Ź –Ķ—Č—Ď –ĺ–ī–Ĺ–į –≥—Ä—É–Ņ–Ņ–į –≤ —ć—ā–ĺ–ľ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–Ķ, –Ĺ–į–∑—č–≤–į–Ķ–ľ–į—Ź Dnd (–ł–Ľ–ł Dnv), –ļ–ĺ—ā–ĺ—Ä–į—Ź –ł–ľ–Ķ–Ķ—ā –≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ—č–Ķ –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ—č–Ķ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł, —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–ł–Ķ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—É—é –ĺ—Ā—Ć –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź, –Ĺ–ĺ –≤–ľ–Ķ—Ā—ā–ĺ –≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –∑–Ķ—Ä–ļ–į–Ľ–į –ĺ–Ĺ–į –ł–ľ–Ķ–Ķ—ā –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł—é, –ļ–ĺ—ā–ĺ—Ä–į—Ź –ļ–ĺ–ľ–Ī–ł–Ĺ–ł—Ä—É–Ķ—ā –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –ł –≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ –Ĺ–į —É–≥–ĺ–Ľ 180¬į/n. Dnh —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–Ļ (n+2)-—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–Ļ –Ņ—Ä–ł–∑–ľ—č –ł –ī–Ľ—Ź –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–Ļ (2n)-—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–Ļ –Ī–ł–Ņ–ł—Ä–į–ľ–ī—č. Dnd —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ī–Ľ—Ź –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–Ļ (n+2)-—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–Ļ –į–Ĺ—ā–ł—Ä–Ņ—Ä–ł–∑–ľ—č, –į —ā–į–ļ–∂–Ķ –ī–Ľ—Ź –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ (2n)-—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–≥–ĺ —ā—Ä–į–Ņ–Ķ—Ü–ĺ—ć–ī—Ä–į. Dn —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —á–į—Ā—ā–ł—á–Ĺ–ĺ –Ņ–ĺ–≤—Ď—Ä–Ĺ—É—ā–ĺ–Ļ –Ņ—Ä–ł–∑–ľ—č. –ď—Ä—É–Ņ–Ņ—č D2 –ł D2h –∑–į–ľ–Ķ—á–į—ā–Ķ–Ľ—Ć–Ĺ—č —ā–Ķ–ľ, —á—ā–ĺ –≤ –Ĺ–ł—Ö –Ĺ–Ķ—ā —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö –ĺ—Ā–Ķ–Ļ –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź. –ė–ľ–Ķ–Ķ—ā—Ā—Ź —ā—Ä–ł –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č–Ķ –ĺ—Ā–ł –Ņ–ĺ—Ä—Ź–ī–ļ–į 2 [2]. D2 —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–ĺ–Ļ –Ņ–ĺ–Ľ–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ—č—Ö —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ (—Ā–ľ. –Ĺ–ł–∂–Ķ), –į D2h —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–ĺ–Ļ –Ņ–ĺ–Ľ–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ—č—Ö —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ Th –ł Oh. D2 –ľ–ĺ–∂–Ĺ–ĺ –ĺ–Ī–Ĺ–į—Ä—É–∂–ł—ā—Ć –≤ –≥–ĺ–ľ–ĺ—ā–Ķ—ā—Ä–į–ľ–Ķ—Ä–į—Ö, —ā–į–ļ–ł—Ö –ļ–į–ļ –ļ–ĺ–Ĺ–ļ–į–Ĺ–į–≤–į–Ľ–ł–Ĺ –ź, –≤ —ā–Ķ—ā—Ä–į—ć–ī—Ä–į–Ľ—Ć–Ĺ—č—Ö –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č—Ö —Ā–ĺ–Ķ–ī–ł–Ĺ–Ķ–Ĺ–ł—Ź—Ö —Ā —á–Ķ—ā—č—Ä—Ć–ľ—Ź –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤—č–ľ–ł —Ö–ł—Ä–į–Ľ—Ć–Ĺ—č–ľ–ł –Ľ–ł–≥–į–Ĺ–ī–į–ľ–ł[–į–Ĺ–≥–Ľ.], –ł–Ľ–ł –≤ –ľ–ĺ–Ľ–Ķ–ļ—É–Ľ–į—Ö, —ā–į–ļ–ł—Ö –ļ–į–ļ —ā–Ķ—ā—Ä–į–ļ–ł—Ā (—Ö–Ľ–ĺ—Ä—Ą—ā–ĺ—Ä–ľ–Ķ—ā–ł–Ľ)–ľ–Ķ—ā–į–Ĺ, –Ķ—Ā–Ľ–ł –≤—Ā–Ķ —Ö–Ľ–ĺ—Ä—Ą—ā–ĺ—Ä–ľ–Ķ—ā–ł–Ľ–ĺ–≤—č–Ķ –≥—Ä—É–Ņ–Ņ—č –ł–ľ–Ķ—é—ā –ĺ–ī–Ĺ—É –ł —ā—É –∂–Ķ —Ö–ł—Ä–į–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć. –≠–Ľ–Ķ–ľ–Ķ–Ĺ—ā—č D2 –Ĺ–į—Ö–ĺ–ī—Ź—ā—Ā—Ź –≤ 1-–ļ-2 —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–ł —Ā –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź–ľ–ł, –∑–į–ī–į–Ĺ–Ĺ—č–ľ–ł –ĺ–Ī—Ä–į—ā–ł–ľ—č–ľ–ł —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ–ł –ļ–≤–į—ā–Ķ—Ä–Ĺ–ł–ĺ–Ĺ–ĺ–≤ –õ–ł–Ņ—ą–ł—Ü–į. –ď—Ä—É–Ņ–Ņ–į Sn –Ņ–ĺ—Ä–ĺ–∂–ī–į–Ķ—ā—Ā—Ź –ļ–ĺ–ľ–Ī–ł–Ĺ–į—Ü–ł–Ķ–Ļ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź –≤ –≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –Ĺ–į —É–≥–ĺ–Ľ 360¬į/n. –Ē–Ľ—Ź –Ĺ–Ķ—á—Ď—ā–Ĺ—č—Ö n –≥—Ä—É–Ņ–Ņ–į —Ā–ĺ–≤–Ņ–į–ī–į–Ķ—ā —Ā –≥—Ä—É–Ņ–Ņ–ĺ–Ļ, –Ņ–ĺ—Ä–ĺ–∂–ī—Ď–Ĺ–Ĺ–ĺ–Ļ –ī–≤—É–ľ—Ź –ĺ—ā–ī–Ķ–Ľ—Ć–Ĺ—č–ľ–ł Cnh –Ņ–ĺ—Ä—Ź–ī–ļ–į 2n, –į –Ņ–ĺ—ā–ĺ–ľ—É –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ Sn –Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ—č–ľ. –Ē–Ľ—Ź —á—Ď—ā–Ĺ—č—Ö n, –ĺ–ī–Ĺ–į–ļ–ĺ, –ĺ–Ĺ–ł —Ä–į–∑–Ľ–ł—á–Ĺ—č –ł –ł–ľ–Ķ—é—ā –Ņ–ĺ—Ä—Ź–ī–ļ–ł n. –ü–ĺ–ī–ĺ–Ī–Ĺ–ĺ Dnd –≥—Ä—É–Ņ–Ņ–į —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –Ĺ–Ķ—Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–Ĺ—č—Ö –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ[–į–Ĺ–≥–Ľ.], –Ĺ–ĺ –Ĺ–Ķ —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł—Ö –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ. –í—Ā–Ķ –≥—Ä—É–Ņ–Ņ—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –≤ 7 –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö —Ā–Ķ—Ä–ł—Ź—Ö —Ä–į–∑–Ľ–ł—á–Ĺ—č, –∑–į –ł—Ā–ļ–Ľ—é—á–Ķ–Ĺ–ł–Ķ–ľ —Ā–Ľ–Ķ–ī—É—é—Č–ł—Ö —á–Ķ—ā—č—Ä—Ď—Ö —Ä–į–≤–Ĺ—č—Ö –Ņ–į—Ä:
S2 ‚ÄĒ —ć—ā–ĺ –≥—Ä—É–Ņ–Ņ–į –Ņ–ĺ—Ä—Ź–ī–ļ–į 2 —Ā –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ —ā–ĺ—á–ļ–ł (Ci ) –ó–ī–Ķ—Ā—Ć "–†–į–≤–Ĺ—č–Ļ" –ĺ–∑–Ĺ–į—á–į–Ķ—ā —ā–ĺ—ā –∂–Ķ —Ā–į–ľ—č–Ļ —Ā —ā–ĺ—á–Ĺ–ĺ—Ā—ā—Ć—é –ī–ĺ —Ā–ĺ–Ņ—Ä—Ź–∂—Ď–Ĺ–Ĺ–ĺ—Ā—ā–ł –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ. –≠—ā–ĺ —Ā—ā—Ä–ĺ–∂–Ķ, —á–Ķ–ľ ¬ę—Ā —ā–ĺ—á–Ĺ–ĺ—Ā—ā—Ć—é –ī–ĺ –į–Ľ–≥–Ķ–Ī—Ä–į–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ł–∑–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ–į¬Ľ. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā —ā—Ä–ł —Ä–į–∑–Ľ–ł—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –Ņ–ĺ—Ä—Ź–ī–ļ–į –ī–≤–į –≤ –Ņ–Ķ—Ä–≤–ĺ–ľ —Ā–ľ—č—Ā–Ľ–Ķ, –Ĺ–ĺ —ā–ĺ–Ľ—Ć–ļ–ĺ –ĺ–ī–Ĺ–į –≤–ĺ –≤—ā–ĺ—Ä–ĺ–ľ. –ü–ĺ–ī–ĺ–Ī–Ĺ—č–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –≥—Ä—É–Ņ–Ņ–į S2n –į–Ľ–≥–Ķ–Ī—Ä–į–ł—á–Ķ—Ā–ļ–ł –ł–∑–ĺ–ľ–ĺ—Ä—Ą–Ĺ–į Z2n. –ď—Ä—É–Ņ–Ņ—č –ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
–ü—Ä–ł–Ĺ–ł–ľ–į—Ź n —Ä–į–≤–Ĺ—č–ľ ‚ąě, –Ņ–ĺ–Ľ—É—á–ł–ľ –≥—Ä—É–Ņ–Ņ—É —Ā –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č–ľ–ł –ĺ—Ā–Ķ–≤—č–ľ–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź–ľ–ł:
–°–Ķ–ľ—Ć –ĺ—Ā—ā–į–≤—ą–ł—Ö—Ā—Ź —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ–ě—Ā—ā–į–≤—ą–ł–Ķ—Ā—Ź —ā–ĺ—á–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –ł–ľ–Ķ—é—ā –ĺ—á–Ķ–Ĺ—Ć –≤—č—Ā–ĺ–ļ—É—é –ł–Ľ–ł –Ņ–ĺ–Ľ–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ—É—é —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –ĺ–Ĺ–ł –ł–ľ–Ķ—é—ā –Ī–ĺ–Ľ–Ķ–Ķ –ĺ–ī–Ĺ–ĺ–Ļ –ĺ—Ā–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –Ņ–ĺ—Ä—Ź–ī–ļ–į, –Ī–ĺ–Ľ—Ć—ą–Ķ–≥–ĺ 2. –ó–ī–Ķ—Ā—Ć Cn –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā –ĺ—Ā—Ć –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –Ĺ–į 360¬į/n, –į Sn –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā –ĺ—Ā—Ć –Ĺ–Ķ—Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –Ĺ–į —ā–ĺ—ā –∂–Ķ —É–≥–ĺ–Ľ. –í —Ā—ā–ĺ–Ľ–Ī—Ü–Ķ –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ —É–ļ–į–∑–į–Ĺ—č –ĺ—Ä–Ī–ł—Ą–ĺ–Ľ–ī–Ĺ–į—Ź –Ĺ–ĺ—ā–į—Ü–ł—Ź[–į–Ĺ–≥–Ľ.] (–≤ –ļ—Ä—É–≥–Ľ—č—Ö —Ā–ļ–ĺ–Ī–ļ–į—Ö), –Ĺ–ĺ—ā–į—Ü–ł—Ź –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į[–į–Ĺ–≥–Ľ.] (–ī–ł–į–≥—Ä–į–ľ–ľ–į –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į), –Ņ–ĺ–Ľ–Ĺ–į—Ź —Ā–ł–ľ–≤–ĺ–Ľ–ł–ļ–į –ď–Ķ—Ä–ľ–į–Ĺ–į ‚ÄĒ –ú–ĺ–≥–Ķ–Ĺ–į –ł —Ā–ĺ–ļ—Ä–į—Č–Ķ–Ĺ–Ĺ–į—Ź —Ą–ĺ—Ä–ľ–į, –Ķ—Ā–Ľ–ł –ĺ–Ĺ–į –ĺ—ā–Ľ–ł—á–Ĺ–į. –°–Ņ–ł—Ā–ĺ–ļ –ļ—Ä—É–Ņ–Ņ:
–Ě–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł, —Ā–≤—Ź–∑–į–Ĺ–Ĺ—č–ľ–ł —Ā —ć—ā–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ, —Ź–≤–Ľ—Ź—é—ā—Ā—Ź:
–ö–į–ļ –∑–į–ľ–Ķ—á–Ķ–Ĺ–ĺ –≤—č—ą–Ķ –ī–Ľ—Ź –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ, –Ľ—é–Ī–ĺ–Ļ —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ –ĺ–Ī—ä–Ķ–ļ—ā, –ł–ľ–Ķ—é—Č–ł–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é K, –Ī—É–ī–Ķ—ā –ł–ľ–Ķ—ā—Ć –ł —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é Kh. –°–≤—Ź–∑—Ć –ľ–Ķ–∂–ī—É –ĺ—Ä–Ī–ł—Ą–ĺ–Ľ–ī–Ĺ–ĺ–Ļ –Ĺ–ĺ—ā–į—Ü–ł–Ķ–Ļ –ł –Ņ–ĺ—Ä—Ź–ī–ļ–ĺ–ľ–ü–ĺ—Ä—Ź–ī–ĺ–ļ –Ľ—é–Ī–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č —Ä–į–≤–Ķ–Ĺ 2, –ī–Ķ–Ľ—Ď–Ĺ–Ĺ–ĺ–Ķ –Ĺ–į –ĺ—Ä–Ī–ł—Ą–ĺ–Ľ–ī–Ĺ—É—é —ć–Ļ–Ľ–Ķ—Ä–ĺ–≤—É —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ—É. –ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ—Ź—Ź —Ä–į–≤–Ĺ–į 2 –ľ–ł–Ĺ—É—Ā —Ā—É–ľ–ľ–į –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –≤—č—á–ł—Ā–Ľ—Ź—é—ā—Ā—Ź –Ņ–ĺ —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –Ņ—Ä–į–≤–ł–Ľ–į–ľ:
–≠—ā–ĺ –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ł–ľ–Ķ–Ĺ–ł—ā—Ć —ā–į–ļ–∂–Ķ –ī–Ľ—Ź –≥—Ä—É–Ņ–Ņ –ĺ–Ī–ĺ–Ķ–≤ –ł –≥—Ä—É–Ņ–Ņ –Ī–ĺ—Ä–ī—é—Ä–ĺ–≤ ‚ÄĒ –ī–Ľ—Ź –Ĺ–ł—Ö —Ā—É–ľ–ľ–į —Ä–į–≤–Ĺ–į 2, —á—ā–ĺ –ī–į—Ď—ā –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–Ļ –Ņ–ĺ—Ä—Ź–ī–ĺ–ļ. –°–ľ. –ĺ—Ä–Ī–ł—Ą–ĺ–Ľ–ī–Ĺ–į—Ź —ć–Ļ–Ľ–Ķ—Ä–ĺ–≤–į —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–į[–į–Ĺ–≥–Ľ.]. –ď—Ä—É–Ņ–Ņ—č –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł–Ļ –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į–Ę–ĺ—á–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł–Ļ –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź —ā–į–ļ–∂–Ķ –≥—Ä—É–Ņ–Ņ–į–ľ–ł –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į –ł –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –∑–į–ī–į–Ĺ—č –ī–ł–į–≥—Ä–į–ľ–ľ–į–ľ–ł –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į ‚ÄĒ –Ē—č–Ĺ–ļ–ł–Ĺ–į, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā –Ĺ–į–Ī–ĺ—Ä –∑–Ķ—Ä–ļ–į–Ľ, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—Č–ł—Ö—Ā—Ź –≤ –ĺ–ī–Ĺ–ĺ–Ļ —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ —ā–ĺ—á–ļ–Ķ, –ł –ĺ–≥—Ä–į–Ĺ–ł—á–ł–≤–į—é—Č–ł—Ö –ī–ĺ–ľ–Ķ–Ĺ–Ĺ—É—é –ĺ–Ī–Ľ–į—Ā—ā—Ć –≤ –≤–ł–ī–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł —Ā—Ą–Ķ—Ä—č. –ď—Ä—É–Ņ–Ņ—č –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į —Ā –ľ–Ķ–Ĺ–Ķ–Ķ —á–Ķ–ľ 3 –ĺ–Ī—Ä–į–∑—É—é—Č–ł–ľ–ł –ł–ľ–Ķ—é—ā –≤—č—Ä–ĺ–∂–ī–Ķ–Ĺ–Ĺ—č–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ –ī–ĺ–ľ–Ķ–Ĺ—č, —ā–į–ļ–ł–Ķ –ļ–į–ļ –Ľ—É–Ĺ–ĺ—á–ļ–į[–į–Ĺ–≥–Ľ.] –ł–Ľ–ł –Ņ–ĺ–Ľ—É—Ā—Ą–Ķ—Ä–į. –í –Ĺ–ĺ—ā–į—Ü–ł–ł –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į[–į–Ĺ–≥–Ľ.] —ā–į–ļ–ł–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —ā–Ķ—ā—Ä–į—ć–ī—Ä–į–Ľ—Ć–Ĺ–į—Ź —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź [3,3], –ĺ–ļ—ā–į—ć–ī—Ä–į–Ľ—Ć–Ĺ–į—Ź —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź[–į–Ĺ–≥–Ľ.] [4,3], –ł–ļ–ĺ—Ā–į—ć–ī—Ä–į–Ľ—Ć–Ĺ–į—Ź —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź [5,3] –ł –ī–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ–į—Ź —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź[–į–Ĺ–≥–Ľ.] [p,2]. –ß–ł—Ā–Ľ–ĺ –∑–Ķ—Ä–ļ–į–Ľ –≤ –Ĺ–Ķ–Ņ—Ä–ł–≤–ĺ–ī–ł–ľ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–Ķ —Ä–į–≤–Ĺ–ĺ nh/2, –≥–ī–Ķ h ‚ÄĒ —á–ł—Ā–Ľ–ĺ –ö–ĺ–ļ—Ā—ā–Ķ—Ä–į –≥—Ä—É–Ņ–Ņ—č, n ‚ÄĒ —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć (3) [3].
–ď—Ä—É–Ņ–Ņ—č –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ–ď—Ä—É–Ņ–Ņ–į–ľ–ł –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ, —ā.–Ķ. –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–ľ–ł –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–į–ľ–ł SO(3), —Ź–≤–Ľ—Ź—é—ā—Ā—Ź: —Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–ł–Ķ –≥—Ä—É–Ņ–Ņ—č Cn (–≥—Ä—É–Ņ–Ņ—č –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ł—Ö –Ņ–ł—Ä–į–ľ–ł–ī), –ī–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č Dn (–≥—Ä—É–Ņ–Ņ—č –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č—Ö –Ņ—Ä–ł–∑–ľ –ł–Ľ–ł –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ł—Ö –Ī–ł–Ņ–ł—Ä–į–ľ–ł–ī) –ł –≥—Ä—É–Ņ–Ņ—č –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ T, O –ł I –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā–Ķ—ā—Ä–į—ć–ī—Ä–į, –ĺ–ļ—ā–į—ć–ī—Ä–į/–ļ—É–Ī–į –ł –ł–ļ–ĺ—Ā–į—ć–ī—Ä–į/–ī–ĺ–ī–Ķ–ļ–į—ć–ī—Ä–į. –í —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, –ī–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č D3, D4 –ł —ā.–ī. —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–į–ľ–ł –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ł—Ö –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č—Ö –ľ–Ĺ–ĺ–≥–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤, –≤–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—č—Ö –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ, –ł —ā–į–ļ–ł–Ķ —Ą–ł–≥—É—Ä—č –ľ–ĺ–∂–Ĺ–ĺ —Ā—á–ł—ā–į—ā—Ć –≤—č—Ä–ĺ–∂–ī–Ķ–Ĺ–Ĺ—č–ľ–ł –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č–ľ–ł –Ņ—Ä–ł–∑–ľ–į–ľ–ł. –ü–ĺ—ć—ā–ĺ–ľ—É –ĺ–Ĺ–ł –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź –ī–ł—ć–ī—Ä–į–ľ–ł (–Ņ–ĺ-–≥—Ä–Ķ—á–Ķ—Ā–ļ–ł: —ā–Ķ–Ľ–ĺ —Ā –ī–≤—É–ľ—Ź –≥—Ä–į–Ĺ—Ź–ľ–ł), —á—ā–ĺ –ł –ĺ–Ī—ä—Ź—Ā–Ĺ—Ź–Ķ—ā –Ĺ–į–∑–≤–į–Ĺ–ł–Ķ –ī–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į.
–ď—Ä—É–Ņ–Ņ–į –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –ĺ–Ī—ä–Ķ–ļ—ā–į —Ä–į–≤–Ĺ–į –Ķ–≥–ĺ –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–Ķ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —ā–ĺ–≥–ī–į –ł —ā–ĺ–Ľ—Ć–ļ–ĺ —ā–ĺ–≥–ī–į, –ļ–ĺ–≥–ī–į –ĺ–Ī—ä–Ķ–ļ—ā —Ö–ł—Ä–į–Ľ–Ķ–Ĺ. –°–Ņ–ł—Ā–ĺ–ļ –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –Ņ–ĺ –ł—Ö –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź–ľ –®—Ď–Ĺ—Ą–Ľ–ł—Ā–į, –Ĺ–ĺ—ā–į—Ü–ł–ł –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į[–į–Ĺ–≥–Ľ.], (–ĺ—Ä–Ī–ł—Ą–ĺ–Ľ–ī–Ĺ–ĺ–Ļ –Ĺ–ĺ—ā–į—Ü–ł–ł[–į–Ĺ–≥–Ľ.]):
–°–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –≥—Ä—É–Ņ–Ņ –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ –ł –ī—Ä—É–≥–ł—Ö –≥—Ä—É–Ņ–Ņ–°–Ľ–Ķ–ī—É—é—Č–ł–Ķ –≥—Ä—É–Ņ–Ņ—č —Ā–ĺ–ī–Ķ—Ä–∂–į—ā —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ—É—é —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é:
–ö–į–ļ –ĺ–Ī—ä—Ź—Ā–Ĺ–Ķ–Ĺ–ĺ –≤—č—ą–Ķ, –ł–ľ–Ķ–Ķ—ā—Ā—Ź 1-–≤-1 —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ľ–Ķ–∂–ī—É —ć—ā–ł–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł –ł –≤—Ā–Ķ–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ:
–Ē—Ä—É–≥–ł–Ķ –≥—Ä—É–Ņ–Ņ—č —Ā–ĺ–ī–Ķ—Ä–∂–į—ā –ļ–ĺ—Ā–≤–Ķ–Ĺ–Ĺ—č–Ķ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł, –Ĺ–ĺ –Ĺ–Ķ —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ—É—é —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é:
–í—Ā–Ķ –ĺ–Ĺ–ł —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—ā –≥—Ä—É–Ņ–Ņ–Ķ –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ H –ł –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–Ķ L —Ā –ł–Ĺ–ī–Ķ–ļ—Ā–ĺ–ľ 2 –≤ —ā–ĺ–ľ —Ā–ľ—č—Ā–Ľ–Ķ, —á—ā–ĺ –ĺ–Ĺ–ł –Ņ–ĺ–Ľ—É—á–į—é—ā—Ā—Ź –ł–∑ H –Ņ—É—ā—Ď–ľ –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł—Ź –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ –≤ H \ L, –ļ–į–ļ –ĺ–Ī—ä—Ź—Ā–Ĺ–Ķ–Ĺ–ĺ –≤—č—ą–Ķ:
–ú–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ—č–Ķ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł–°—É—Č–Ķ—Ā—ā–≤—É—é—ā –ī–≤–Ķ –ī–ł—Ā–ļ—Ä–Ķ—ā–Ĺ—č–Ķ —ā–ĺ—á–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č —Ā–ĺ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ, —á—ā–ĺ –Ĺ–ł–ļ–į–ļ–į—Ź –ī–ł—Ā–ļ—Ä–Ķ—ā–Ĺ–į—Ź —ā–ĺ—á–Ķ—á–Ĺ–į—Ź –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–į –Ĺ–Ķ –ł–ľ–Ķ–Ķ—ā –ł—Ö –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ —Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ—č ‚ÄĒ Oh –ł Ih. –ė—Ö –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą–į—Ź –ĺ–Ī—Č–į—Ź –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–į ‚ÄĒ Th. –Ē–≤–Ķ –≥—Ä—É–Ņ–Ņ—č –Ņ–ĺ–Ľ—É—á–į—é—ā—Ā—Ź –ł–∑ –Ĺ–Ķ—Ď –Ņ—É—ā—Ď–ľ –∑–į–ľ–Ķ–Ĺ—č –≤—Ä–į—Č–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –Ņ–ĺ—Ä—Ź–ī–ļ–į 2 –Ĺ–į —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é –Ņ–ĺ—Ä—Ź–ī–ļ–į 4 –ł –ī–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–ł–Ķ–ľ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –Ņ–ĺ—Ä—Ź–ī–ļ–į 5 —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ę–į–ļ–∂–Ķ –ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ–Ľ—É—á–ł—ā—Ć –ī–≤–Ķ –≥—Ä—É–Ņ–Ņ—č –Ņ—É—ā—Ď–ľ –ī–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–ł—Ź –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ—č—Ö –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–Ķ–Ļ –≤ Th. –°—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –ī–≤–Ķ –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ķ —ā–ĺ—á–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č —Ā–ĺ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ, —á—ā–ĺ –Ĺ–ł–ļ–į–ļ–į—Ź –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–į—Ź —ā–ĺ—á–Ķ—á–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į –Ĺ–Ķ —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā –ł—Ö –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ —Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ—č ‚ÄĒ Oh –ł D6h. –ė—Ö –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ—č–Ķ –ĺ–Ī—Č–ł–Ķ –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ—č, –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ĺ—ā –ĺ—Ä–ł–Ķ–Ĺ—ā–į—Ü–ł–ł, ‚ÄĒ D3d –ł D2h. –£–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–ł–Ķ –≥—Ä—É–Ņ–Ņ –Ņ–ĺ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ĺ–ľ—É —ā–ł–Ņ—É –≥—Ä—É–Ņ–Ņ—č–Ē–į–Ľ–Ķ–Ķ –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ—č–Ķ –≤—č—ą–Ķ –≥—Ä—É–Ņ–Ņ—č —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ—č –Ņ–ĺ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ĺ–ľ—É —ā–ł–Ņ—É –≥—Ä—É–Ņ–Ņ—č. –Ě–į–ł–ľ–Ķ–Ĺ—Ć—ą–ł–Ķ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č, –Ĺ–Ķ —Ź–≤–Ľ—Ź—é—Č–ł–Ķ—Ā—Ź –≥—Ä—É–Ņ–Ņ–į–ľ–ł —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ ‚ÄĒ –≥—Ä—É–Ņ–Ņ–į –ļ–≤–į—ā–Ķ—Ä–Ĺ–ł–ĺ–Ĺ–ĺ–≤ (–Ņ–ĺ—Ä—Ź–ī–ļ–į 8), Z3 √ó Z3 (–Ņ–ĺ—Ä—Ź–ī–ļ–į 9), –ī–ł—Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–į—Ź –≥—Ä—É–Ņ–Ņ–į Dic3 (–Ņ–ĺ—Ä—Ź–ī–ļ–į 12) –ł 10 –ł–∑ 14 –≥—Ä—É–Ņ–Ņ –Ņ–ĺ—Ä—Ź–ī–ļ–į 16. –°—ā–ĺ–Ľ–Ī–Ķ—Ü "–ß–ł—Ā–Ľ–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤ –Ņ–ĺ—Ä—Ź–ī–ļ–į 2" –≤ –Ņ–ĺ—Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ —ā–į–Ī–Ľ–ł—Ü–Ķ –Ņ–ĺ–ļ–į–∑—č–≤–į–Ķ—ā –ĺ–Ī—Č–Ķ–Ķ —á–ł—Ā–Ľ–ĺ –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł —ā–ł–Ņ–į C2, Ci, Cs. –≠—ā–ĺ –ĺ–Ī—Č–Ķ–Ķ —á–ł—Ā–Ľ–ĺ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ–ī–Ĺ–ĺ–Ļ –ł–∑ —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ, –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź—é—Č–ł—Ö —Ä–į–∑–Ľ–ł—á–ł—ā—Ć –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ—č–Ķ —ā–ł–Ņ—č –≥—Ä—É–Ņ–Ņ, –≤ —ā–ĺ –≤—Ä–Ķ–ľ—Ź –ļ–į–ļ –ł—Ö —ā–ł–Ņ –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–ł –Ņ–ĺ–ľ–ĺ–≥–į–Ķ—ā —Ä–į–∑–Ľ–ł—á–ł—ā—Ć –≥—Ä—É–Ņ–Ņ—č –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ —ā–ĺ–Ļ –∂–Ķ —Ā–į–ľ–ĺ–Ļ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č. –°—Ä–Ķ–ī–ł –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č—Ö –ł–∑–ĺ–ľ–Ķ—ā—Ä–ł–Ļ –≥—Ä—É–Ņ–Ņ –į —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ľ–Ĺ–ĺ–≥–ĺ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ—č—Ö —ā–ł–Ņ–ĺ–≤ –≥—Ä—É–Ņ–Ņ —Ā 0, 1 –ł 3 —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ–ł –Ņ–ĺ—Ä—Ź–ī–ļ–į 2, —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –ī–≤–Ķ –≥—Ä—É–Ņ–Ņ—č —Ā 2n + 1 —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ–ł –Ņ–ĺ—Ä—Ź–ī–ļ–į 2 –ł —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā —ā—Ä–ł –≥—Ä—É–Ņ–Ņ—č —Ā 2n + 3 —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ–ł –Ņ–ĺ—Ä—Ź–ī–ļ–į 2 (–ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ n ‚Č• 2 ). –Ě–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —á—Ď—ā–Ĺ–ĺ–≥–ĺ —á–ł—Ā–Ľ–į —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤ –Ņ–ĺ—Ä—Ź–ī–ļ–į 2.
–ď—Ä—É–Ņ–Ņ—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ, —Ź–≤–Ľ—Ź—é—Č–ł–Ķ—Ā—Ź —Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–ł–ľ–ł –ļ–į–ļ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č–ď—Ä—É–Ņ–Ņ–į —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –Ņ–ĺ—Ä—Ź–ī–ļ–į n ‚ÄĒ —ć—ā–ĺ Cn. –ē—Ď —ā–ł–Ņ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č ‚ÄĒ —Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–į—Ź –≥—Ä—É–Ņ–Ņ–į Zn, –ļ–ĺ—ā–ĺ—Ä–į—Ź –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā—Ā—Ź —ā–į–ļ–∂–Ķ –ļ–į–ļ Cn. –ě–ī–Ĺ–į–ļ–ĺ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ķ—Č—Ď –ī–≤–į –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö —Ä—Ź–ī–į –≥—Ä—É–Ņ–Ņ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —Ā —ā–ł–Ņ–į–ľ–ł –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ:
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤—č–ī–Ķ–Ľ—Ź—Ź –∂–ł—Ä–Ĺ—č–ľ —ą—Ä–ł—Ą—ā–ĺ–ľ 10 –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł—Ö —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ, –ī–Ľ—Ź –ļ–ĺ—ā–ĺ—Ä—č—Ö –Ņ—Ä–ł–ľ–Ķ–Ĺ–ł–ľ–į –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ķ –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł—Ź[–į–Ĺ–≥–Ľ.], –ľ—č –ł–ľ–Ķ–Ķ–ľ:
–ł —ā.–ī. –ď—Ä—É–Ņ–Ņ—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ, –ī–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ—č–Ķ –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ–í –ī–≤—É—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ –ī–ł—ć–ī—Ä–ł—á–Ķ—Ā–ļ–į—Ź –≥—Ä—É–Ņ–Ņ–į Dn –≤–ļ–Ľ—é—á–į–Ķ—ā –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ľ–ĺ–∂–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–į–ļ –Ņ–Ķ—Ä–Ķ–≤–ĺ—Ä–į—á–ł–≤–į–Ĺ–ł–Ķ –ĺ–Ī—ä–Ķ–ļ—ā–į –Ī–Ķ–∑ —Ä–į–∑–Ľ–ł—á–Ķ–Ĺ–ł—Ź –Ľ–ł—Ü–Ķ–≤–ĺ–Ļ –ł –ĺ–Ī—Ä–į—ā–Ĺ–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č. –ě–ī–Ĺ–į–ļ–ĺ –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ –ī–≤–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —Ä–į–∑–Ľ–ł—á–Ĺ—č ‚ÄĒ –≥—Ä—É–Ņ–Ņ–į —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —Ā –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ–ľ Dn —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā n –ĺ—Ā–Ķ–Ļ –Ņ–ĺ—Ä—Ź–ī–ļ–į 2, –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č—Ö –ļ –ĺ—Ā—Ź–ľ –Ņ–ĺ—Ä—Ź–ī–ļ–į n, –į –Ĺ–Ķ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź. Dn —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–ĺ–Ļ –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ n-—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–Ļ –Ņ—Ä–ł–∑–ľ—č —Ā –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č–ľ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ, n-—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–Ļ –Ī–ł–Ņ–ł—Ä–į–ľ–ł–ī—č —Ā –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č–ľ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ, –į —ā–į–ļ–∂–Ķ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–Ļ n-—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–Ļ –į–Ĺ—ā–ł–Ņ—Ä–ł–∑–ľ—č –ł –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ n-—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–≥–ĺ —ā—Ä–į–Ņ–Ķ—Ü–ĺ—ć–ī—Ä–į. –ď—Ä—É–Ņ–Ņ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–į–ļ–∂–Ķ –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —ā–į–ļ–ł—Ö –ĺ–Ī—ä–Ķ–ļ—ā–ĺ–≤, –Ķ—Ā–Ľ–ł —Ā–ī–Ķ–Ľ–į—ā—Ć –ł—Ö —Ö–ł—Ä–į–Ľ—Ć–Ĺ—č–ľ–ł –Ņ—É—ā—Ď–ľ —Ä–į–∑–ľ–Ķ—ā–ļ–ł –≥—Ä–į–Ĺ–Ķ–Ļ –ł–Ľ–ł –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –ľ–ĺ–ī–ł—Ą–ł–ļ–į—Ü–ł–ł —Ą–ł–≥—É—Ä—č. –ź–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī–ł—ć–ī—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ Dihn, –ļ–ĺ—ā–ĺ—Ä–į—Ź –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā—Ā—Ź —ā–į–ļ–∂–Ķ —Ā–ł–ľ–≤–ĺ–Ľ–ĺ–ľ Dn. –ě–ī–Ĺ–į–ļ–ĺ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ķ—Č—Ď —ā—Ä–ł –≥—Ä—É–Ņ–Ņ—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —Ā —ā–ĺ–Ļ –∂–Ķ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ:
–ó–į–ľ–Ķ—ā—Ć—ā–Ķ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ:
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤—č–ī–Ķ–Ľ—Ź—Ź 12 –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł—Ö –≥—Ä—É–Ņ–Ņ –∂–ł—Ä–Ĺ—č–ľ —ą—Ä–ł—Ą—ā–ĺ–ľ –ł –∑–į–Ņ–ł—Ā—č–≤–į—Ź D1d –ļ–į–ļ —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā C2h, –ľ—č –ł–ľ–Ķ–Ķ–ľ:
–ł —ā.–ī. –Ē—Ä—É–≥–ĺ–ĶC2n,h –Ņ–ĺ—Ä—Ź–ī–ļ–į 4n —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —ā–ł–Ņ–į Z2n √ó Z2. –Ē–Ľ—Ź n = 1 –ľ—č –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ Dih2, –≥—Ä—É–Ņ–Ņ—É, —É–∂–Ķ –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ—É—é –≤—č—ą–Ķ, —ā–į–ļ —á—ā–ĺ n ‚Č• 2. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤—č–ī–Ķ–Ľ—Ź—Ź 2 —Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ķ —ā–ĺ—á–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –∂–ł—Ä–Ĺ—č–ľ —ą—Ä–ł—Ą—ā–ĺ–ľ, –ľ—č –ł–ľ–Ķ–Ķ–ľ:
–ł —ā.–ī. Dnh –Ņ–ĺ—Ä—Ź–ī–ļ–į 4n —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —ā–ł–Ņ–į Dihn √ó Z2. –Ē–Ľ—Ź –Ĺ–Ķ—á—Ď—ā–Ĺ—č—Ö n –≥—Ä—É–Ņ–Ņ–į —É–∂–Ķ –ĺ–Ņ–ł—Ā–į–Ĺ–į –≤—č—ą–Ķ, —ā–į–ļ —á—ā–ĺ –ľ—č –∑–ī–Ķ—Ā—Ć –ł–ľ–Ķ–Ķ–ľ D2nh –Ņ–ĺ—Ä—Ź–ī–ļ–į 8n, –ļ–ĺ—ā–ĺ—Ä–į—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —ā–ł–Ņ–į Dih2n √ó Z2 (n‚Č•1). –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤—č–ī–Ķ–Ľ—Ź—Ź 3 –ī–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ—č–Ķ –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ķ —ā–ĺ—á–Ķ—á–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č –∂–ł—Ä–Ĺ—č–ľ —ą—Ä–ł—Ą—ā–ĺ–ľ, –ľ—č –ł–ľ–Ķ–Ķ–ľ:
–ł —ā.–ī. –ě—Ā—ā–į—ą–ł–Ķ—Ā—Ź —Ā–Ķ–ľ—Ć –≥—Ä—É–Ņ–Ņ, –≥–ī–Ķ 5 –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł—Ö —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ –≤—č–ī–Ķ–Ľ–Ķ–Ĺ—č –∂–ł—Ä–Ĺ—č–ľ —ą—Ä–ł—Ą—ā–ĺ–ľ:
–Ě–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č–Ķ –ī–ł—Ā–ļ—Ä–Ķ—ā–Ĺ—č–Ķ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł–ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –ĺ–Ī–∑–ĺ—Ä —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ł—Ā—á–Ķ—Ä–Ņ—č–≤–į—é—Č–ł–ľ, –ĺ–Ĺ –Ņ–ĺ–ļ–į–∑—č–≤–į–Ķ—ā –Ĺ–Ķ—Ź–≤–Ĺ–ĺ, –ļ–į–ļ–ł–Ķ —Ā–Ľ—É—á–į–ł –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –ī–ł—Ā–ļ—Ä–Ķ—ā–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä:
–ė —ā.–ī.. –Ď–ł–Ĺ–į—Ä–Ĺ—č–Ķ –Ņ–ĺ–Ľ–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č–ě—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ Spin(3) ‚Üí SO(3) —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī–≤–ĺ–Ļ–Ĺ—č–ľ –Ņ–ĺ–ļ—Ä—č—ā–ł–Ķ–ľ –≥—Ä—É–Ņ–Ņ—č –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ —Ā–Ņ–ł–Ĺ–ĺ—Ä–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ. (–≠—ā–ĺ –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ķ —Ā–≤—Ź–∑–Ĺ–ĺ–Ķ –Ņ–ĺ–ļ—Ä—č—ā–ł–Ķ SO(3), –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É Spin(3) –ĺ–ī–Ĺ–ĺ—Ā–≤—Ź–∑–Ĺ–į.) –ü–ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ĺ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–ł[–į–Ĺ–≥–Ľ.] —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ď–į–Ľ—É–į –ľ–Ķ–∂–ī—É –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–į–ľ–ł Spin(3) –ł –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–į–ľ–ł SO(3) (—ā–ĺ—á–Ķ—á–Ĺ—č–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź) ‚ÄĒ –ĺ–Ī—Ä–į–∑ –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ—č –≥—Ä—É–Ņ–Ņ—č Spin(3) —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–ĺ—á–Ķ—á–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ, –į –Ņ—Ä–ĺ–ĺ–Ī—Ä–į–∑ —ā–ĺ—á–Ķ—á–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č Spin(3). –ü—Ä–ĺ–ĺ–Ī—Ä–į–∑ –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–Ļ —ā–ĺ—á–Ķ—á–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ī–ł–Ĺ–į—Ä–Ĺ–ĺ–Ļ –Ņ–ĺ–Ľ–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ, –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā—Ā—Ź –ļ–į–ļ <l,n,m>, –ł –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —ā–Ķ–ľ –∂–Ķ –ł–ľ–Ķ–Ĺ–Ķ–ľ, —á—ā–ĺ –ł —ā–ĺ—á–Ķ—á–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į, –Ĺ–ĺ —Ā –ī–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–ł–Ķ–ľ –Ī–ł–Ĺ–į—Ä–Ĺ–į—Ź, –Ņ—Ä–ł —ć—ā–ĺ–ľ –Ņ–ĺ—Ä—Ź–ī–ĺ–ļ –≥—Ä—É–Ņ–Ņ—č —É–ī–≤–į–ł–≤–į–Ķ—ā—Ā—Ź –Ņ–ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—é –ļ —Ā–≤—Ź–∑–į–Ĺ–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–Ķ –ľ–Ĺ–ĺ–≥–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į (l,m,n). –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ņ—Ä–ĺ–ĺ–Ī—Ä–į–∑–ĺ–ľ –ł–ļ–ĺ—Ā–į—ć–ī—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č[–į–Ĺ–≥–Ľ.] (2,3,5) —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ī–ł–Ĺ–į—Ä–Ĺ–į—Ź –ł–ļ–ĺ—Ā–į—ć–ī—Ä–į–Ľ—Ć–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į, <2,3,5>. –Ď–ł–Ĺ–į—Ä–Ĺ—č–Ķ –Ņ–ĺ–Ľ–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č:
–ď—Ä—É–Ņ–Ņ—č —Ā–ł—Ā—ā–Ķ–ľ–į—ā–ł–∑–ł—Ä–ĺ–≤–į–Ĺ—č —Ā–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—Ü–ł–ł ADE[–į–Ĺ–≥–Ľ.] –ł —Ą–į–ļ—ā–ĺ—Ä–≥—Ä—É–Ņ–Ņ–ĺ–Ļ C2 –Ņ–ĺ –ī–Ķ–Ļ—Ā—ā–≤–ł—é –Ī–ł–Ĺ–į—Ä–Ĺ–ĺ–Ļ –Ņ–ĺ–Ľ–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č –ł–ľ–Ķ–Ķ—ā —Ā–ł–Ĺ–≥—É–Ľ—Ź—Ä–Ĺ–ĺ—Ā—ā—Ć –Ē—É –í–į–Ľ–į[–į–Ĺ–≥–Ľ.] [4]. –Ē–Ľ—Ź —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ, –ĺ–Ī—Ä–į—Č–į—é—Č–ł—Ö –ĺ—Ä–ł–Ķ–Ĺ—ā–į—Ü–ł—é, —Ā–ł—ā—É–į—Ü–ł—Ź —Ā–Ľ–ĺ–∂–Ĺ–Ķ–Ķ, —ā–į–ļ –ļ–į–ļ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –ī–≤–Ķ Pin-–≥—Ä—É–Ņ–Ņ—č[–į–Ĺ–≥–Ľ.], —ā–į–ļ —á—ā–ĺ –ł–ľ–Ķ–Ķ—ā—Ā—Ź –ī–≤–Ķ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č–Ķ –Ī–ł–Ĺ–į—Ä–Ĺ—č–Ķ –≥—Ä—É–Ņ–Ņ—č, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ķ –ī–į–Ĺ–Ĺ–ĺ–Ļ —ā–ĺ—á–Ķ—á–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–Ķ. –ó–į–ľ–Ķ—ā–ł–ľ, —á—ā–ĺ —ć—ā–ĺ –Ņ–ĺ–ļ—Ä—č—ā–ł–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–ļ—Ä—č—ā–ł–Ķ–ľ –≥—Ä—É–Ņ–Ņ, –Ĺ–Ķ –Ņ–ĺ–ļ—Ä—č—ā–ł–Ķ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤. –°–ľ. —ā–į–ļ–∂–Ķ
–ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł—Ź
–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į
–°—Ā—č–Ľ–ļ–ł
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia