ジョンソン円

  ジョンソン円 J_A ≅ J_B ≅ J_C（半径R、交点はHとA, B, C）

  A, B, Cを通る円（半径R）

  △ABCジョンソンのジョンソン三角形△J_AJ_BJ_C

  △J_AJ_BJ_C の外接円（半径R)

ジョンソン円（ジョンソンえん、英: Johnson circles）は、幾何学において共通の点Hで交わり、同じ半径Rを持つ3つの円である。この図ではHの他、3円のうち2円のHでない方の交点が計3つ存在する（ただし、いずれかの2円が接する場合、その2円の交点はHとする。いずれかの2円が完全に一致する場合は、その交点をHの対蹠点とする）。この3点は基準三角形[1]（reference triangle）と呼ばれる三角形を定義する。ジョンソン円はロジャー・アーサー・ジョンソンに因んで命名された[2][3][4]。

性質

  ジョンソン円 J_A ≅ J_B ≅ J_C（半径R、交点はHとA, B, C）

  △ABCの逆補三角形の外接円（半径は2R、ジョンソン円にP_A, P_B, P_Cで接する。

  共点HとP_A, P_B, P_Cを結ぶ直線

  △ABCの逆補三角形 △P_AP_BP_C

1. ジョンソン円の中心は、中心H、半径Rの円上にある。また、ジョンソン円の中心はジョンソン三角形（Johnson triangle）をなす。
2. 中心H,半径2Rの円、逆補円はジョンソン円に接する。3つの接点はHをジョンソン三角形の頂点で鏡映した点となる。
3. ジョンソン円と逆補円の接点は、基準三角形の逆補三角形を成す。これはHを中心にジョンソン三角形を2倍拡大した図形である。
4. ジョンソンの定理:3つのジョンソン円のうち2つの（Hでない）交点（基準三角形の頂点）は半径Rの円周上にある。この定理はルーマニアで、ゲオルゲ・ティツェイカ（英語版）のThe 5 lei coin problemで知られている。
5. 基準三角形はジョンソン三角形と合同である。
6. 点Hは基準三角形の垂心、ジョンソン三角形の外心になる。
7. ジョンソン三角形と基準三角形の相似の中心は、ジョンソン三角形と基準三角形の共通の九点中心（英語版）（九点円の中心）であり、九点中心に-1倍拡大の関係にある。

証明

性質1はジョンソン円の定義から自明。性質2は中心P,半径Rの円上に点Pを中心とする半径2Rの円は元の円に接することから分かる。性質3は性質2と相似性より証明できる。

性質4,5は、2つのジョンソン円が割線（接する場合は共通内接線）で鏡映の関係にあること、この鏡映で逆補三角形の2頂点も入れ替わることより示される。2つのジョンソン円の交点は逆補三角形の辺の中点であり、Hはその垂直二等分線上にある。つまり、基準三角形は逆補三角形の中点三角形であるからその相似と相似比½が分かる（相似中心は重心）。ところで、逆補円の半径は2Rなので、基準三角形の外接円の半径はRとなる。

性質6は性質4,5の垂直二等分線の所の事実により、垂心の定義と一致する（逆補三角形の辺の垂直二等分線が基準三角形の頂垂線となる）ことから分かる。

性質7は性質6より即座に示される。基準三角形とジョンソン三角形の相似比が-1なので、相似中心は基準三角形の外心Oとジョンソン三角形の垂心Hの中点である。九点円の中心は外心と垂心の中点であるという有名事実よりその中点は双方の九点中心と一致する。

ジョンソンの定理の証明は代数的な処理も存在する。長さRの3つのベクトル${\displaystyle {\vec {u}},{\vec {v}},{\vec {w}},}$を用意し、ジョンソン円の中心は ${\displaystyle H+{\vec {u}},H+{\vec {v}},H+{\vec {w}}.}$と表せる。このとき2つのジョンソン円の交点はそれぞれ${\displaystyle H+{\vec {u}}+{\vec {v}},H+{\vec {u}}+{\vec {w}},H+{\vec {v}}+{\vec {w}}}$である。点${\displaystyle H+{\vec {u}}+{\vec {v}}+{\vec {w}}}$は点${\displaystyle H+{\vec {u}}+{\vec {v}},H+{\vec {u}}+{\vec {w}},H+{\vec {v}}+{\vec {w}}}$とR 離れていることより示される。

更なる性質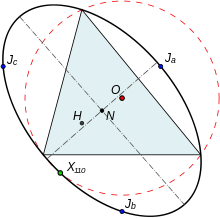

ジョンソン外接円錐曲線

ジョンソン三角形の頂点を通る外接三次曲線

ジョンソン円は基準三角形の外接円を3辺で鏡映したものとしてみることができる。更に、鏡映においてHは基準三角形の外接円上に移る。Hの3辺による鏡映点が成す三角形は circum-orthic triangleと呼ばれる。基準三角形の外心Oの3辺による鏡映点はジョンソン三角形の頂点になる。オイラー線の鏡映はX(110)、キーペルト放物線の焦点で交わる。 ジョンソン三角形と基準三角形は共通の九点円を持つ。またこの2三角形の頂点は同一円錐曲線上、ジョンソン外接円錐曲線（Johnson circumconic）上にある。中心は九点中心でX(216) などを曲線上に持つ。外接円との第四交点はX(110)である。

また、ジョンソン三角形と基準三角形の頂点、そして外心、垂心、九点中心を通る外接三次曲線が2つ存在する。一つ目は first Musselman cubic, K026である。この三次曲線はジョンソン三角形の中点三角形の頂点も通る。二つ目は、Euler central cubic, K044である。この三次曲線はジョンソン三次曲線の垂心三角形の頂点も通る。

脚注

出典

1. エヴァン・チェン『数学オリンピック幾何への挑戦: ユークリッド幾何学をめぐる船旅』日本評論社、2023年2月。ISBN 978-4-535-78978-4。https://books.google.co.jp/books/about/%E6%95%B0%E5%AD%A6%E3%82%AA%E3%83%AA%E3%83%B3%E3%83%94%E3%83%83%E3%82%AF%E5%B9%BE%E4%BD%95%E3%81%B8%E3%81%AE%E6%8C%91.html?id=yMWGzwEACAAJ&redir_esc=y。 
2. Roger Arthur Johnson, Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle, Houghton, Mifflin Company, 1929
3. Roger Arthur Johnson, "A Circle Theorem", American Mathematical Monthly 23, 161–162, 1916.
4. Roger Arthur Johnson (1890–1954) Archived 2014-09-13 at the Wayback Machine.

外部リンク

• Weisstein, Eric W. "Johnson Theorem". mathworld.wolfram.com (英語).
• F. M. Jackson and Weisstein, Eric W. "Johnson Circles". mathworld.wolfram.com (英語).
• F. M. Jackson and Weisstein, Eric W. "Johnson Triangle". mathworld.wolfram.com (英語).
• Weisstein, Eric W. "Johnson Circumconic". mathworld.wolfram.com (英語).
• Weisstein, Eric W. "Anticomplementary Triangle". mathworld.wolfram.com (英語).
• Weisstein, Eric W. "Circum-Orthic Triangle". mathworld.wolfram.com (英語).
• Bernard Gibert Circumcubic K026
• Bernard Gibert Circumcubic K044
• Clark Kimberling, "Encyclopedia of triangle centers". (Lists some 3000 interesting points associated with any triangle.)