割線

初等幾何学における曲線の割線[1]（かっせん、かつせん、英: secant line, secant[注 1]; 正割線）は、その曲線と（相異なる）ふたつ以上の点で交わる直線を言う[2]:62。 割線を意味する英語の secant はラテン語: secare に由来し、「割ること」(to cut) の意である[3]:167。円の割線の場合、円と割線はちょうど二点で交わり、それら二点を結ぶ線分は円の弦になる—すなわち、円の割線から円によって切り取られる区間が円の弦である[4]:387。

円の割線

→「弦 (数学)」も参照
割線など円においてしばしば現れる線分および直線

直線と円は二点または一点で交わるか、さもなくば交わらないかである。二点で交わる直線を割線、一点で交わる直線を接線、交点を持たない直線は外線 (exterior line; 外部直線)と言う。円の弦とは円周上の相異なる二点を結ぶ線分のことであったから、任意の弦は割線に一意的に延長され、逆に任意の割線は円の弦を一意的に定める。

平面幾何の厳密で現代的な取り扱いにおいては、明らかであると思われるような結果や、ユークリッドが『原論』において（断りなく）仮定していたような結果も、ふつうは証明される。例えば

定理 (Elementary Circular Continuity)
[5]:229
円 C と直線 l が与えられたとき、直線 l が C の内側の点 A と外側の点 B を含むならば、l は C の割線である。

状況によっては弦に関する主張を割線に関する主張として述べたほうが記述が統一的になりすっきりするということも起きる。そのような例として

命題[6]:482
与えられた円の弦 AB および CD を含む二つの割線が、円周上にない点 P で交わるならば、線分の長さに関して AP⋅PB = CP⋅PD が満足される。

を考えよう。点 P が円の内側にある場合は『原論』の第III巻の35であるが、P が円の外側にある場合については『原論』に記述はない。しかし、ロバート・シムソンはクリストファー・クラヴィウスに従い、彼らのユークリッドについての解説書において、こんにち割線・割線定理（英語版）とも呼ばれるこの結果を示した[7]:73。

曲線の割線

曲線の割線は円の割線ほどは単純でなく、相異なる二点で曲線と交わる直線はさらにほかの点でもその曲線と交わる可能性がある分、より複雑である。文献によっては「曲線の割線とは曲線と相異なる二点で交わる直線である」と定義することもあるが、この定義ではその直線が曲線とほかの点で交わる可能性については特に制限を課してはいないのだから、このように述べるならば（円ではほかの点で交わる可能性がないというだけのことであって）円の割線も曲線の割線もその定義は同一であるということができる。

割線と接線

曲線上の適当な点 P において接線が存在するときには、割線はその点における曲線の接線を近似するのに用いることができる。曲線上の二点 P, Q から定まる曲線の割線について、P は固定して Q だけ動かすものと仮定する。Q が曲線に沿って P に近づくとき、割線の傾きが一定の値に近づくならば、その極限値によって点 P における接線の傾きが定まり[2]、割線 PQ は接線に限りなく近づく。微分積分学において、これが微分係数の幾何学的な定義である。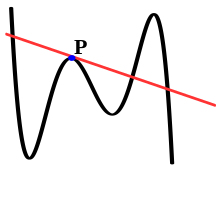

点 P におけるこの接線は曲線の割線にもなっている

さて点 P における接線はその曲線の割線にもなり得る（点 P における接線が接点以外でその曲線と少なくとも一つの交点を持つときはそうである）。このようなことが起きる理由として、「接線である」ことは曲線上の接点 P のごく小さな近傍にだけ依存する「局所的」性質であるのに対して、「割線である」ことはその曲線を与える函数の定義域全体を調べなければならない「大域的」性質であるということを理解するのがよい。

点集合と多点割線

割線の概念はユークリッド空間よりももっと一般の設定のもとで考えることができる。何らかの幾何学的設定の下で、k 個の点からなる有限集合 K を考えるとき、与えられた直線が K の n-点割線 (n-secant) であるとは、それが　K の点をちょうど n 個含むときに言う[8]:70。例えば K をユークリッド平面内の一つの円周上に並べられた50個の点の集合とするとき、それらの点の任意のふたつを結ぶ直線は二点割線 (2-secant, bisecant) であり、それらの点のひとつだけを通る直線は単点割線 (1-secant, unisecant) と言う。この例において、単点割線は基にした円の接線でなくともよいことに注意すべきである。

このような用語法は結合幾何（英語版）や離散幾何ではよく用いられる。実例として、結合幾何におけるシルヴェスター–ガライの定理は、ユークリッド幾何の n 点が共線でないならば、それら点に関する二点割線が存在しなければならないことを述べる。また、離散幾何の果樹園植栽問題（英語版）のもともとは、与えられた有限点集合の三点割線の総数の上界を求めるものであった。

この定義において、各直線とその集合が有限個の点でのみ交わる限りは、その点集合自体が有限集合となることは本質的ではない。

脚注

[脚注の使い方]

注釈

  1. ^ 三角函数の secant（正割函数 sec）と同じ語だが、日本語では混乱の恐れはあるまい

出典

  1. ^ 『割線』 - コトバンク
  2. ^ a b Protter, Murray H.; Protter, Philip E. (1988), Calculus with Analytic Geometry, Jones & Bartlett Learning, ISBN 9780867200935 
  3. ^ Redgrove, Herbert Stanley (1913), Experimental Mensuration: An Elementary Test-book of Inductive Geometry, Van Nostrand 
  4. ^ Gullberg, Jan (1997), Mathematics: From the Birth of Numbers, W. W. Norton & Company, ISBN 9780393040029 
  5. ^ Venema, Gerard A. (2006), Foundations of Geometry, Pearson/Prentice-Hall, ISBN 978-0-13-143700-5 
  6. ^ Jacobs, Harold R. (1974), Geometry, W. H. Freeman & Co., ISBN 0-7167-0456-0 
  7. ^ Heath, Thomas L. (1956), The thirteen books of Euclid's Elements (Vol. 2), Dover 
  8. ^ Hirschfeld, J. W. P. (1979), Projective Geometries over Finite Fields, Oxford University Press, ISBN 0-19-853526-0 

関連項目

外部リンク