赤い線分 BX はこの円の弦 である。(線分 AB は円の直径) 初等幾何学 における円 の弦 (げん、英 : chord [ 注釈 1] 線分 を言う。弦を無限に延長して得られる直線 を、割線 と呼ぶ。より一般に、任意の曲線 (例えば楕円 )において、その曲線上の二点を結ぶ線分を、その曲線上の弦と総称する。円の中心を通る弦はその円の直径 である。任意の直径は弦であるが、任意の弦が直径となるわけではない。
直径 (Diameter) 半径 (Radius) 弦 (Chord) 割線 (Secant) 接線 (Tangent)
円の弦に関する性質には、例えば以下のようなものがある:
二つの弦が、円の中心から等距離にあるための必要十分条件は、それら弦の長さが等しいことである。
長さの等しい弦を、円の中心から見込む角(中心角)は等しい。
円の中心を通る弦は直径と呼ばれ、その円の最長の弦である。
弦 AB および CD を延長して得られる割線 が点 P で交わるならば、それらの長さは AP·PB = CP·PD 方冪の定理 )。
楕円 における互いに平行な弦の族が与えられたとき、それら弦の中点はすべて同一直線上にある [ 1]
三角法 の初期の段階では弦が手広く用いられていた。知られた最古の三角函数表はヒッパルコス の編纂した弦の数表 (英語版 ) ° 刻みで弦函数の値が書き並べられていた。AD 2世紀に、アレクサンドリアのプトレマイオス は、天文学に関する著書『アルマゲスト 』において、より詳細な弦の数表を編纂している(0.5°から180°まで0.5°刻みで値が与えられ、これは円の直径を120として小数点以下60進ふた桁まで正確であった)[ 2]
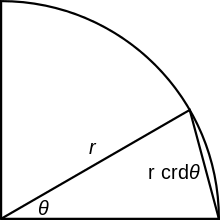
中心角 θ に対する弦; 弦の半分が正弦 弦函数 crd は幾何学的には(図のように)中心角 θ の見込む弦の長さが r ⋅crd(θ )r は半径)となるように定義される。すなわち、弦函数の値 crd(θ ) は、中心角 θ によって隔てられた単位円 上の二点間を結ぶ弦の長さ である。ここでは角度 θ は正の向きに測るものとし、弧度法で区間 0 < θ ≤ π の範囲に入るものと考えている。この元函数 crd をより現代的な正弦函数 sin と関連付けることができる。それには、一点 (1, 0) ともう一つの点 (cos(θ ), sin(θ )) を結ぶ弦の長さを三平方の定理 を用いて計算すればよい。すると
crd
θ
=
(
1
−
cos
θ
)
2
+
sin
2
θ
=
2
−
2
cos
θ
=
2
sin
(
θ
2
)
{\displaystyle \operatorname {crd} \theta ={\sqrt {(1-\cos \theta )^{2}+\sin ^{2}\theta }}={\sqrt {2-2\cos \theta }}=2\sin \!{\Bigl (}{\frac {\theta }{2}}{\Bigr )}}
[ 2] 半角公式 による。
現代的な三角法が正弦函数に基づいて構築されているのと同様に、古来の三角法はこの弦函数をもとに構築されていた。ヒッパルコスは(いまではもうすべて失われたけれども)12巻にも及ぶ弦についての文献を書き上げたというから、三角法についてはかなりのことが知られていたと考えられる。現代的な三角函数に関するよく知られた恒等式の弦函数版がある:
恒等式
正弦版
弦版
三平方の定理
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
crd
2
θ
+
crd
2
(
π
−
θ
)
=
4
{\displaystyle \operatorname {crd} ^{2}\theta +\operatorname {crd} ^{2}(\pi -\theta )=4}
半角公式
sin
θ
2
=
±
1
−
cos
θ
2
{\displaystyle \sin {\frac {\theta }{2}}=\pm {\sqrt {\frac {1-\cos \theta }{2}}}}
crd
θ
2
=
±
2
−
crd
(
π
−
θ
)
{\displaystyle \operatorname {crd} \ {\frac {\theta }{2}}=\pm {\sqrt {2-\operatorname {crd} (\pi -\theta )}}}
辺心距離 a
c
=
2
r
2
−
a
2
{\displaystyle c=2{\sqrt {r^{2}-a^{2}}}}
c
=
D
2
−
4
a
2
{\displaystyle c={\sqrt {D^{2}-4a^{2}}}}
中心角 θ
c
=
2
r
sin
(
θ
2
)
{\displaystyle c=2r\sin \!{\Big (}{\frac {\theta }{2}}{\Bigr )}}
c
=
D
2
crd
θ
{\displaystyle c={\frac {D}{2}}\operatorname {crd} \theta }
ただし、半径 r (直径 D )の円の中心角 θ が見込む弦の長さを c とする。
弦函数 crd の逆函数 acrd もまた存在して、逆正弦函数とは
acrd
(
y
)
=
2
arcsin
(
y
2
)
{\displaystyle \operatorname {acrd} (y)=2\arcsin \!{\Big (}{\frac {y}{2}}{\Bigr )}}
[ 3]
^ 弓弦を意味するラテン語 : chorda
^ Chakerian, G. D. (1979). “7”. In Honsberger, R.. A Distorted View of Geometry . Washington, DC, USA: Mathematical Association of America . p. 147 ^ a b Maor, Eli (1998), Trigonometric Delights , Princeton University Press, pp. 25-27, ISBN 978-0-691-15820-4
^ Simpson, David G. (2001年11月8日). “AUXTRIG ”. Greenbelt, Maryland, USA: NASA Goddard Space Flight Center. 2015年10月26日 閲覧。
ウィキメディア・コモンズには、
弦 (数学) に関連するカテゴリがあります。