|
Quadratur des Kreises Die Quadratur des Kreises ist ein klassisches Problem der Geometrie. Die Aufgabe besteht darin, aus einem gegebenen Kreis mit Zirkel und Lineal in endlich vielen Schritten ein Quadrat gleichen Flächeninhalts zu konstruieren, sprich die Konstruktion eines Quadrats mit der Seitenlänge . Sie ist äquivalent zur sogenannten Rektifikation des Kreises, also der Konstruktion einer geraden Strecke, die dem Kreisumfang entspricht. Das wiederum entspricht der Konstruktion der Kreiszahl (halber Kreisumfang) aus der Strecke, deren Länge gleich Längenmaßeinheit ist. Beschränkt man die Konstruktionsmittel auf Zirkel und Lineal, so ist die Aufgabe aufgrund der Transzendenz von unlösbar. Erst im Jahre 1882 konnte dies von dem deutschen Mathematiker Ferdinand von Lindemann bewiesen werden. Die Quadratur des Kreises gehört zu den populärsten Problemen der Mathematik. Jahrhundertelang suchten neben Mathematikern auch immer wieder Laien vergeblich nach einer Lösung. Der Begriff Quadratur des Kreises ist in vielen Sprachen zu einer Metapher für eine unlösbare Aufgabe geworden. GeschichteVorgeschichte Ein Kreis mit Durchmesser 9 in einem Quadrat der Seitenlänge 9, das in neun kleinere Quadrate der Seitenlänge 3 zerlegt wird. Der Flächeninhalt des Kreises entspricht ungefähr dem eines (unregelmäßigen) Achtecks (7·9) und etwas genauer dem eines Quadrats mit Seitenlänge 8 (64). Bereits in den altorientalischen Hochkulturen gab es Verfahren zur Berechnung von Kreisflächen. Beispielsweise wird im Papyrus Rhind (um 1550 v. Chr.) der Durchmesser des Kreises in 9 Teile geteilt. Sein genauer Flächeninhalt in diesen Einheiten ist . Dieser Wert wird dann durch ein Quadrat (im Bild rot) der Kantenlänge 8 angenähert, also durch (siehe hierzu Aus dem Papyrus Rhind). In einem zweiten Verfahren wird der Kreis durch ein unregelmäßiges Achteck angenähert. Dazu werden von dem 9×9-Quadrat, in das er einbeschrieben ist, an allen vier Ecken gleiche Dreiecke mit zusammen 18 Flächeneinheiten abgeschnitten, sodass 63 übrig bleiben. Derartige Musterlösungen waren aus der Praxis gewonnen und für die Praxis bestimmt, es gab keine weitergehenden theoretischen Überlegungen, insbesondere wurde kein Unterschied zwischen exakter Lösung und Näherung gemacht.[1] Eine deduktive Vorgehensweise in der Mathematik, bei der durch Beweise gestützte Sätze die Musteraufgaben ersetzen, entwickelte sich ab dem 6. Jahrhundert v. Chr. in Griechenland. Ansatzweise ist sie schon bei Thales von Milet, deutlicher in der von Pythagoras von Samos gegründeten Schule der Pythagoreer zu erkennen.[2] Mit der gemeinhin dem Pythagoreer Hippasos von Metapont zugeschriebenen Entdeckung inkommensurabler Strecken im späten 6. oder frühen 5. Jahrhundert v. Chr. stellte sich heraus, dass es konstruierbare Objekte gibt (beispielsweise die Diagonale eines Quadrats), die nicht als ganzzahliges Verhältnis darstellbar sind. Dies schien bemerkenswert, da die einzigen bekannten Arten von Zahlen die ganzen Zahlen und die Verhältnisse ganzer Zahlen (im heutigen Sprachgebrauch die „rationalen Zahlen“) waren. Beliebige geometrische Strecken mussten dementsprechend stets kommensurabel sein, also in einem ganzzahligen Längenverhältnis zueinander stehen. Durch die Entdeckung waren nun Längen geometrisch konstruierbar, die arithmetisch nicht als „Zahl“ im bisherigen Sinn darstellbar waren (im heutigen Sprachgebrauch handelt es sich um „irrationale Zahlen“). Die Geometrie konnte plötzlich mehr darstellen, als die Arithmetik es vermochte.[3][4] Als Folge dieser Entdeckung trat die Arithmetik zugunsten der Geometrie in den Hintergrund, Gleichungen mussten jetzt geometrisch gelöst werden, etwa durch Aneinanderlegung von Figuren und Überführung verschiedener Figuren in Rechtecke oder Quadrate. Aus dem späten 5. Jahrhundert stammen die drei klassischen Konstruktionsprobleme der antiken Mathematik, neben der Quadratur des Kreises noch die Aufgabe der Dreiteilung des Winkels und das Delische Problem der Verdoppelung des Würfels.[5] Eine Beschränkung der Konstruktionsmittel auf Zirkel und Lineal wurde dabei nicht generell gefordert. Während der Beschäftigung mit den klassischen Problemen wurden schon früh Lösungen gefunden, die auf weitergehenden Hilfsmitteln basieren. Allerdings kristallisierte sich im Lauf der Zeit eine Haltung heraus, die eine möglichst weitgehende Beschränkung verlangt. Spätestens bei Pappos war diese weitestgehende Beschränkung zur Maßregel geworden.[6][7] Frühe ArbeitenAls einer der ersten soll dem griechischen Schriftsteller Plutarch zufolge der Philosoph Anaxagoras „im Gefängnis die Quadratur des Kreises aufgeschrieben (oder: gezeichnet, altgriechisch ἔγραφε)“ haben,[8] nähere Angaben zu Anaxagoras’ Konstruktion macht Plutarch nicht. Ein Gefängnisaufenthalt des Anaxagoras wäre auf etwa 430 v. Chr. zu datieren, als der Philosoph in Athen wegen Gottlosigkeit angeklagt war.[9] Ausführlichere Quellen zu den Anfängen der Forschung sind hauptsächlich spätantike Kommentare zu Werken des Aristoteles, Schriften also, die mit einer zeitlichen Distanz von rund 900 Jahren entstanden sind. Dementsprechend unsicher sind zeitliche Reihenfolge und genaue Gedankengänge der ersten Ansätze. Die wichtigsten Arbeiten des 5. Jahrhunderts v. Chr. stammen von Hippokrates von Chios, Antiphon, Bryson von Herakleia und Hippias von Elis.[10]  Die Überführung von Dreiecken in Rechtecke, von Rechtecken in Quadrate (Quadratur des Rechtecks) oder die Addition zweier Quadrate (Satz des Pythagoras) war mit den bekannten geometrischen Sätzen bereits damals elementar zu bewältigen. Hippokrates von Chios konnte um 440 v. Chr. ein Beispiel für eine krummlinig begrenzte Fläche geben, die exakt in ein Quadrat überführt werden konnte. Ausgehend von dem bei ihm noch als Axiom benutzten Satz, dass sich die Flächeninhalte ähnlicher Kreissegmente wie die Quadrate über ihren Sehnen verhalten, gelang es Hippokrates, von Kreisbögen begrenzte Flächen, die sogenannten „Möndchen des Hippokrates“, zu quadrieren.[11] Die Quadratur des Kreises ist auf diese Weise jedoch nicht zu erreichen, da nur bestimmte Möndchen – zum Beispiel die über der Seite des Quadrats, nicht jedoch die über der Seite eines regelmäßigen Sechsecks – quadrierbar sind. Dass Dreiecke (und damit beliebige Vielecke) in ein Quadrat übergeführt werden konnten, war ein zweiter Ansatz, ein dem Kreis flächengleiches Polygon zu konstruieren. Antiphon hatte die Idee, den Kreis durch einbeschriebene Vielecke anzunähern. Bryson von Herakleia verfeinerte dieses Vorgehen, indem er den Kreis zusätzlich durch umbeschriebene Vielecke näherte und einen Zwischenwert bildete.[12] Hippias von Elis entwickelte etwa 425 v. Chr. zur Lösung der Winkeldreiteilung eine Kurve, die mechanisch durch die Überlagerung einer kreisförmigen mit einer linearen Bewegung erzeugt wurde. Gut hundert Jahre später entdeckte Deinostratos, dass mithilfe dieser Kurve, der sogenannten Quadratrix, die Strecke der Länge – und damit mithilfe weiterer elementarer Konstruktionen ein Quadrat mit dem Flächeninhalt – konstruiert werden kann. Da die Quadratrix selbst jedoch eine sogenannte transzendente Kurve ist (siehe hierzu Beweis der Unmöglichkeit), also nicht mit Zirkel und Lineal zu erzeugen ist, war die Lösung im strengen Sinne damit nicht erreicht.[13][14] Archimedes Eine ausführliche Abhandlung mit dem Titel Die Kreismessung ist von Archimedes überliefert.[15] Archimedes bewies in dieser Arbeit drei grundlegende Sätze:
Mit dem ersten Satz wurde das Problem der Quadratur des Kreises auf die Frage nach der Konstruierbarkeit des Umfangs eines Kreises aus dem vorgegebenen Radius und damit auf die Konstruierbarkeit von zurückgeführt. Im dritten Satz gab Archimedes gleich eine ebenso einfache wie genaue Näherung dieser Zahl an, nämlich 22⁄7, ein Wert (≈ 3,143), der für praktische Zwecke noch heute Verwendung findet. Der zweite Satz ist ein einfaches Korollar aus den beiden anderen; dass sich der Flächeninhalt eines Kreises proportional zum Quadrat seines Durchmessers verhält, und war bereits Euklid bekannt.[16] Archimedes gab hier den Wert der Proportionalitätskonstanten an. Zum Beweis seiner Aussagen zog Archimedes die Idee des Bryson von Herakleia heran, mit der man eine beliebige Annäherung des Kreises durch ein- und umbeschriebene regelmäßige Polygone erreicht. Ausgehend vom einbeschriebenen Sechseck und umbeschriebenen Dreieck gelangte Archimedes durch sukzessive Verdoppelung der Seitenzahl jeweils beim 96-Eck an. Eine geschickte Abschätzung der in den einzelnen Rechenschritten auftretenden Quadratwurzeln ergab seine in Satz 3 genannten Schranken.[17][18] In einer weiteren Arbeit Über Spiralen[19] beschrieb Archimedes die Konstruktion der später nach ihm benannten archimedischen Spirale, die ähnlich wie Hippias’ Quadratrix durch die Überlagerung einer kreisförmigen mit einer linearen Bewegung gewonnen wird. Er zeigte, dass durch das Anlegen der Tangente an diese Spirale der Umfang eines Kreises auf einer Geraden abgetragen werden kann, wodurch eine Quadratur des Kreises möglich wird. Die (nicht-klassische) Lösung mit seiner Spirale wird im Abschnitt Quadratur des Kreises mithilfe der archimedischen Spirale beschrieben. Wie bei der Quadratrix sind allerdings weder seine Spirale selbst noch etwa ihre Tangente mit Zirkel und Lineal konstruierbar.[20] Mittelalter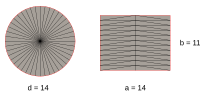 Infolge eines verstärkten Interesses für die antike Mathematik im christlichen Europa ab etwa dem 11. Jahrhundert entstanden etliche Abhandlungen über die Quadratur des Kreises, jedoch ohne dass dabei wesentliche Beiträge zur eigentlichen Lösung geleistet wurden. Als Rückschritt zu betrachten ist, dass im Mittelalter der archimedische Näherungswert von 22⁄7 für die Kreiszahl lange Zeit als exakt galt.[21] Einer der ersten Autoren des Mittelalters, der das Problem der Kreisquadratur wiederaufnahm, war Franco von Lüttich. Um 1050 entstand sein Werk De quadratura circuli.[22] Franco stellt darin zunächst drei Quadraturen vor, die er verwirft. Die ersten beiden geben für die Seitenlänge des Quadrates 7⁄8 beziehungsweise für die Diagonale 10⁄8 des Kreisdurchmessers an, was relativ schlechten Näherungen von 3 1⁄16 und 3 1⁄8 für entspricht. Der dritte Vorschlag wiederum setzt den Umfang des Quadrates dem Kreisumfang gleich, verlangt also die Rektifikation des letzteren. Francos eigene Lösung geht von einem Kreis mit Durchmesser 14 aus. Dessen Fläche setzt er als genau 7² × 22⁄7 = 154 an. Nach Francos Argumentation lässt sich rechnerisch kein flächengleiches Quadrat finden, da die Quadratwurzel aus 22⁄7 irrational ist, als geometrisch konstruierbare inkommensurable Strecke (siehe Vorgeschichte) jedoch liefert die Quadratwurzel aus 22⁄7 die Quadratur. Dazu zerlegt er den Kreis in 44 gleiche Sektoren, die er zu einem Rechteck der Seitenlängen 11 und 14 zusammenfügt. Den nötigen Kunstgriff, bei dem er die Kreissektoren durch rechtwinklige Dreiecke mit Katheten der Länge 1 und 7 ersetzt, erläutert Franco allerdings nicht.[23] Problematisch ist auch sein nicht ganz geglückter Versuch, das Rechteck anschließend durch eine geeignete Zerlegung in ein Quadrat zu überführen. Offensichtlich war Franco das althergebrachte griechische Verfahren nicht geläufig.[23] Spätere Abhandlungen der Scholastik erschöpfen sich mehr oder minder in einer Abwägung der Argumente der bekannten Klassiker. Erst mit der Verbreitung lateinischer Übersetzungen der archimedischen Schriften im Spätmittelalter wurde der Wert 22⁄7 wieder als Näherung erkannt und nach neuen Lösungen des Problems gesucht, so beispielsweise von Nikolaus von Kues. Dieser griff die Idee, den Kreis durch eine Folge regelmäßiger Vielecke mit wachsender Seitenzahl anzunähern, wieder auf, suchte im Gegensatz zu Archimedes jedoch nicht den Kreisumfang, sondern den Kreisradius bei vorgegebenem gleichbleibendem Umfang der Polygone zu bestimmen. In einem Brief an den Arzt und Naturforscher Paolo Toscanelli gab von Kues eine solche Lösung, die er für genau hielt, an. Der daraus ermittelte Wert für die Kreiszahl liegt auch immerhin zwischen den von Archimedes gegebenen Grenzen. Die eigentlichen Arbeiten von Kues zum Thema liefern deutlich schlechtere Näherungen und wurden damit zum Ziel einer Streitschrift des Regiomontanus, der die Ungenauigkeit der Berechnungen nachwies und die Beweise „als philosophische, aber nicht als mathematische“ bezeichnete.[24] Fortschritte der Kreismessung in der frühen NeuzeitAb dem 16. Jahrhundert brachten die Weiterentwicklung des archimedischen Näherungsverfahrens sowie das Aufkommen moderner analytischer Methoden Fortschritte in der Kreisberechnung. Bei der ursprünglichen Methode des Archimedes wird der Kreisumfang durch den Umfang eines dem Kreis einbeschriebenen und den eines dem Kreis umbeschriebenen Vielecks abgeschätzt. Genauere Schranken ergeben sich durch eine Erhöhung der Eckenzahl. Der niederländische Mathematiker Willebrord van Roijen Snell (Snellius) fand heraus, dass auch, ohne die Seitenzahl zu vergrößern, feinere Schranken für die Länge eines Bogenstückes als nur die Sehnen der Polygone angegeben werden können. Er konnte dieses Ergebnis allerdings nicht streng beweisen.[25] Die Ausarbeitung und Verbesserung des snelliusschen Ansatzes leistete Christiaan Huygens in seiner Arbeit De circuli magnitudine inventa,[26] in der er auch den Beweis der von Snellius aufgestellten Sätze erbrachte.[27] Auf rein elementargeometrischem Weg gelang Huygens eine so gute Eingrenzung der zwischen Vieleck und Kreis liegenden Fläche, dass er bei entsprechender Seitenzahl der Polygone die Kreiszahl auf mindestens viermal so viel Nachkommastellen genau erhielt wie Archimedes mit seinem Verfahren.[28] Der rein geometrische Ansatz zur Bestimmung der Kreiskonstanten war mit Huygens’ Arbeit im Wesentlichen ausgeschöpft. Bessere Näherungen ergaben sich mithilfe von unendlichen Reihen, speziell der Reihenentwicklung trigonometrischer Funktionen.[27] Zwar hatte François Viète schon Ende des 16. Jahrhunderts durch die Betrachtung bestimmter Streckenverhältnisse aufeinanderfolgender Polygone eine erste exakte Darstellung von durch ein unendliches Produkt gefunden, doch erwies sich diese Formel als unhandlich. Eine einfachere Reihe, die darüber hinaus nur mit Multiplikationen und Divisionen auskommt, stammt von John Wallis,[29] eine weitere Darstellung der Kreiszahl als Kettenbruch von William Brouncker.[30] Wichtiger für die Praxis war die von James Gregory und davon unabhängig von Gottfried Wilhelm Leibniz gefundene Reihe für den Arcustangens.[31] Obwohl diese Reihe selbst nur langsam konvergiert, kann man aus ihr andere Reihen ableiten, die sich wiederum sehr gut zur Berechnung der Kreiszahl eignen. Anfang des 18. Jahrhunderts waren mithilfe solcher Reihen über 100 Stellen von berechnet,[32] neue Erkenntnisse über das Problem der Kreisquadratur konnten dadurch allerdings nicht gewonnen werden. Algebraische Problemstellung und Irrationalität von π   Zur Lösung des Problems bedurfte es zum einen der Möglichkeit, dem geometrischen Begriff „konstruierbar“ eine algebraische Bedeutung zu geben, zum anderen genauerer Einsicht der Eigenschaften der Kreiszahl. Eine geometrische Konstruktion mit Zirkel und Lineal geht von einer endlichen Anzahl vorgegebener Punkte aus und ermittelt in einer endlichen Anzahl von Schritten neue Punkte durch das Schneiden zweier Geraden, zweier Kreise oder einer Geraden mit einem Kreis. Die Übersetzung dieser Vorgehensweise in die Sprache der Algebra gelang durch die Einführung von Koordinatensystemen im Rahmen der im 17. Jahrhundert hauptsächlich von Pierre de Fermat und René Descartes entwickelten analytischen Geometrie.[33] Geraden und Kreise konnten mit den neuen Mitteln durch Gleichungen beschrieben, Schnittpunkte durch das Lösen von Gleichungssystemen bestimmt werden. Es stellte sich heraus, dass die mit Zirkel und Lineal von einer Strecke der Länge 1 ausgehend konstruierbaren Streckenlängen genau den Zahlen entsprechen, die sich durch eine endliche Zahl von rationalen (Grund-)Operationen (Addition, Subtraktion, Multiplikation und Division) sowie einer endlichen Anzahl aus der Umkehroperation des Quadrierens resultierender Quadratwurzeln aus der Zahl 1 ableiten lassen.[34] Insbesondere entsprechen diese Längen algebraischen Zahlen, also einer Teilmenge der Zahlen, die eine Lösung einer algebraischen Gleichung beliebigen Grades mit rationalen Koeffizienten sind. Zahlen, die nicht algebraisch sind, heißen transzendent. Dem entsprechend sind transzendente Längen ausgehend von der Länge 1 nicht in endlich vielen Schritten mit Zirkel und Lineal konstruierbar.[35][36] Ausgangspunkt für die weiteren Untersuchungen der Kreiszahl waren einige grundlegende Erkenntnisse Leonhard Eulers, die dieser 1748 in seinem Werk Introductio in analysin infinitorum[37] veröffentlicht hatte. Euler stellte unter anderem mit der nach ihm benannten eulerschen Formel erstmals einen Zusammenhang zwischen trigonometrischen Funktionen und der Exponentialfunktion her und lieferte darüber hinaus einige Kettenbruch- und Reihendarstellungen von und der später nach ihm benannten eulerschen Zahl e.[38] Diese Vorarbeit machte sich Johann Heinrich Lambert zunutze, der mithilfe einer der eulerschen Kettenbruchentwicklungen 1766 erstmals zeigen konnte, dass e und irrationale, also nicht durch einen ganzzahligen Bruch darstellbare Zahlen sind.[39] Eine kleine Lücke in Lamberts Beweisführung wurde 1806 von Adrien-Marie Legendre geschlossen, der gleichzeitig den Irrationalitätsbeweis für erbrachte.[40] Die Vermutung, dass nicht algebraisch sein könnte, wurde zumindest von Euler, Lambert und Legendre ausgesprochen. Dennoch war bis zur Mitte des 19. Jahrhunderts noch nicht klar, dass es überhaupt transzendente Zahlen geben musste. Dieser Nachweis gelang 1844/1851 Joseph Liouville durch explizite Konstruktion von transzendenten liouvilleschen Zahlen.[41] Beweis der UnmöglichkeitFerdinand von Lindemann konnte 1882 schließlich beweisen, dass nicht algebraisch, sondern transzendent ist. Deshalb ist in gerader Linie nicht konstruierbar und die Quadratur des Kreises unmöglich.[42] Lindemann griff in seiner Arbeit auf ein Ergebnis des französischen Mathematikers Charles Hermite zurück. Dieser hatte 1873 gezeigt, dass die eulersche Zahl e transzendent ist.[43] Darauf aufbauend konnte Lindemann den sogenannten Satz von Lindemann-Weierstraß beweisen, der besagt, dass für beliebige, voneinander verschiedene algebraische Zahlen und für beliebige algebraische Zahlen die Gleichung nur dann gelten kann, wenn alle den Wert Null haben.[44] Insbesondere kann für keine von Null verschiedene algebraische Zahl z der Ausdruck eine rationale Zahl ergeben. Nach dieser Vorbereitung konnte Lindemann die Annahme, sei algebraisch, mithilfe der eulerschen Identität zum Widerspruch führen; musste somit transzendent sein.[43] Lindemanns Beweis für die Transzendenz von wurde in den folgenden Jahren und Jahrzehnten noch wesentlich vereinfacht, so etwa durch David Hilbert im Jahre 1893.[45] Popularität der KreisquadraturDie Quadratur des Kreises erreichte wie nur wenige andere Fragestellungen auch außerhalb der Mathematik eine große Popularität. Als Folge versuchten sich viele mathematische Laien an der Lösung des einfach erscheinenden Problems; etliche glaubten, sie gefunden zu haben. Berichte über ein wachsendes Aufkommen an Amateurarbeiten ab dem 18. und 19. Jahrhundert und Beispiele zum Thema finden sich bei Jean-Étienne Montucla,[46] Johann Heinrich Lambert[47] und Augustus de Morgan.[48] In der Regel handelte es sich um Verfahren, bei denen das Problem mechanisch, numerisch oder durch eine geometrische Näherungskonstruktion „exakt“ gelöst wurde. Derartige Arbeiten wurden in einer derart großen Zahl an Mathematiker oder wissenschaftliche Institutionen herangetragen, dass sich zum Beispiel die Pariser Akademie der Wissenschaften 1775 genötigt sah, die weitere Untersuchung von vorgeblichen Lösungen der Kreisquadratur offiziell abzulehnen:[49]
Auch nach dem Unmöglichkeitsbeweis durch Lindemann von 1882 wurden noch im 20. Jahrhundert vermeintliche Kreisquadraturen veröffentlicht, die in jüngerer Zeit als vergebliche Versuche der Amateurmathematiker Stoff der Unterhaltungsmathematik geworden sind. Ein Hauptgrund für die gerade für mathematische Laien hohe Attraktivität ist wohl die sehr elementare Problemstellung, die auch ohne tiefergehendes mathematisches Wissen verstanden werden kann oder zumindest verständlich zu sein scheint. Zusammen mit den zahlreichen vergeblichen Lösungsversuchen etablierter Wissenschaftler erlangte die Kreisquadratur einen regelrechten Nimbus.[50] Ein weiterer, nicht zu unterschätzender Grund für die zahlreichen Bemühungen um die Quadratur des Kreises war die verbreitete Meinung, auf die Lösung des Problems sei ein hoher Preis ausgesetzt – ein Irrglaube, der möglicherweise auf die irrige Vermutung zurückgeht, die Kreisquadratur stünde in direkter Verbindung mit dem ebenfalls lange ungelösten Problem der exakten Bestimmung der geographischen Länge zur See, auf dessen Lösung in der Tat Preise ausgesetzt waren. Die Sage von den Preisausschreiben hielt sich so hartnäckig, dass selbst 1891 in Meyers Konversations-Lexikon noch zu lesen war, dass „Karl V. 100.000 Thaler und die holländischen Generalstaaten eine noch höhere Summe“ ausgesetzt hätten.[51] Prominente KreisquadriererProminentes Beispiel für einen Amateurmathematiker, der die Quadratur des Kreises gefunden zu haben glaubte, war der englische Philosoph Thomas Hobbes. Seine 1665 in seinem Werk De corpore veröffentlichte Lösung – in Wirklichkeit eine Näherungskonstruktion – wurde von John Wallis noch im selben Jahr widerlegt. In der Folgezeit entspann sich zwischen den beiden eine in scharfem Tonfall geführte Auseinandersetzung, die erst mit Hobbes’ Tod im Jahr 1679 ein Ende fand.[52] Lambert berichtet von drei Kreisquadraturen mittels eines bestimmten rationalen Wertes. Die in der Mitte des 18. Jahrhunderts erschienenen Arbeiten beruhen auf der Näherung 35⁄31 für das Verhältnis von Kreisdurchmesser zur Seite des flächengleichen Quadrates. Für die Kreiszahl erhält man daraus die Näherung Einem der drei Autoren, dem Prediger Merkel aus Ravensburg, widmete Gotthold Ephraim Lessing das Gedicht „Auf den Herrn M** den Erfinder der Quadratur des Zirkels“.[54] Die Kreisquadratur des amerikanischen Arztes Edward J. Goodwin erschien 1894 sogar im ersten Band des American Mathematical Monthly, wenn auch nur als Annonce des Autors. Die Arbeit selbst ist in sich widersprüchlich und lässt je nach Lesart mehrere Werte für zu. Sie war Grundlage für einen 1897 dem Parlament von Indiana vorgelegten Gesetzentwurf, der sogenannten Indiana Pi Bill, durch den die Erkenntnisse Goodwins zum Gesetz erhoben werden sollten.[55] Kunst und KulturAls frühester Beleg für das Auftauchen eines sogenannten „Kreisquadrierers“ oder „Quadrators“ wird gelegentlich eine Stelle in Aristophanes’ Komödie Die Vögel aus dem 5. Jahrhundert vor Chr. zitiert, in der Meton als Vermesser auftritt und den Grundriss einer neuen Stadt mit geometrischen Hilfsmitteln so festlegen will, dass „der Kreis ein Viereck werde“. Gemeint ist damit jedoch nicht die Quadratur eines Kreises, sondern das Anlegen zweier rechtwinklig aufeinandertreffender Straßen, auch wenn der Ausdruck wie eine Anspielung auf die Kreisquadratur erscheint.[56][57] Im Jahr 1321 stellte Dante Alighieri in seinem Werk Göttliche Komödie das Quadrieren des Kreises als eine Aufgabe dar, die über das menschliche Verständnis hinausgeht und die er mit seiner eigenen Unfähigkeit vergleicht, das Paradies zu verstehen: 
– Dante Alighieri, Ludwig Gottfried Blanc (Übersetzer): Die Göttliche Komödie – Paradies − Gesang 33, Zeilen 133 bis 141[58]  In James Joyce’ wegweisendem Roman Ulysses aus dem Jahr 1922 ist die Hauptfigur Leopold Bloom, seines Zeichens Annoncenakquisiteur. Er arbeitete im Sommer des Jahres 1882 angestrengt an einer Lösung des Problems Die Quadratur des Kreises, um damit ein vermeintlich großes Vermögen zu erhalten. Gegen Ende des Romans musste er sich in einem langen Dialog mit seinem Vater, Rudolf Virág, traurig und enttäuscht eingestehen, dass er versagt hatte.[59][60]
– James Joyce: Ulysses: Roman[59] NäherungskonstruktionenWeil eine exakte Lösung mit Zirkel und Lineal nicht möglich ist, gibt es Näherungskonstruktionen für die Kreisquadratur, die für viele Zwecke exakt genug sind. Einfache, schon in der Antike bekannte Verfahren geben ein ganzzahliges Verhältnis von Durchmesser oder Radius des Kreises zur Seite oder Diagonalen des Quadrates an. Neben der im Papyrus Rhind erwähnten Gleichsetzung des Kreises vom Durchmesser 9 mit dem Quadrat der Seitenlänge 8 war auch die des Kreises vom Durchmesser 8 mit dem Quadrat der Diagonalen 10 bekannt. Beide Verfahren werden im Folgenden beschrieben. Aus dem Papyrus Rhind Die bereits etwa im 16. Jahrhundert v. Chr. im Papyrus Rhind beschriebene und im nebenstehenden Bild nachempfundene Näherungskonstruktion, zählt zu den ältesten. Der Autor – ein Ägypter – des mathematischen Papyrus nimmt als Ansatz die Bestimmung des Kreisdurchmessers für die Seite des Quadrates.[61] Nach dem Ziehen des Kreises mit beliebigem Durchmesser werden die beiden zueinander senkrecht stehenden Mittelachsen des Kreises eingezeichnet. Anschließend teilt man eine Mittelachse in neun gleiche Teile. Auf die zweite Mittelachse werden zwei Mal vier Neuntel des Durchmessers, ausgehend jeweils von der Mitte des Kreises, abgetragen. Schließlich bedarf es noch des Einzeichnens des Quadrates mit der Seitenlänge gleich acht Neuntel des Durchmessers. Das Verhältnis Durchmesser zur Quadratseite entspricht somit dem Wert . Der angenäherte Flächeninhalt des Kreises hat den Wert bzw. . Vergleicht man dies mit einer heute möglichen Bestimmung des Flächeninhalts , so zeigt sich[61]
Bezogen auf den Einheitskreis (Radius ) ergibt sich für die Näherung der Kreiszahl
sowie für den konstruierten Wert der Quadratseite
Dies bedeutet, im Einheitskreis gleichen zwei Nachkommastellen der Seitenlänge des Quadrates denen von . Beispiel zur Veranschaulichung der Fehler:
Babylonisches Verfahren Die folgende Konstruktion findet sich einerseits bei den Babyloniern und andererseits angedeutet in den Veröffentlichungen des römischen Feldmessers Vitruv.[21] Sie liefert den Wert 3 1⁄8 für . Um ein bequemes zeichnerisches Verfahren anzugeben, nimmt Albrecht Dürer diese Konstruktion im Jahr 1525 in seinem Werk Vnderweysung der messung mit dem zirckel und richtscheyt wieder auf. Dürer ist sich dabei bewusst, dass es sich um eine reine Näherungslösung handelt, er schreibt explizit, dass eine exakte Lösung noch nicht gefunden sei:
– Albrecht Dürer: Vnderweysung der messung mit dem zirckel und richtscheyt[62] Konstruktion von Kochański Eine klassische Näherungslösung für den halben Kreisumfang entdeckte der polnische Mathematiker Adam Adamandy Kochański im Jahr 1685. Sie kommt mit nur einer Zirkelöffnung aus. Die eigentliche Konstruktion besteht aus einer Rektifikation des Halbkreises. Kochanski konstruierte aus dem vorgegebenen Radius näherungsweise eine gerade Strecke der Länge d. h. annähernd den halben Kreisumfang Das in der nebenstehenden Zeichnung rot eingezeichnete Rechteck hat folglich mit nahezu den gleichen Flächeninhalt wie der Kreis. Die angenäherte Quadratur folgt daraus elementar mithilfe mathematischer Gesetze des rechtwinkligen Dreiecks, beschrieben in Quadratur des Rechtecks. Die Kreiszahl wird bei Kochański auf vier Nachkommastellen genau angenähert:[63] Der konstruierten Wert der Quadratseite Beispiele zur Veranschaulichung der Fehler:
Konstruktion von Specht mit eingezeichnetem Quadrat ⇒ siehe hierzu in Kreiszahl Im Jahr 1828 veröffentlichte C. G. Specht seine Zweite Annäherungs-Construction des Kreis-Umfanges im Journal für die reine und angewandte Mathematik. Für die Annäherung fand er den Wert[64] Halbiert man diesen Wert, ergibt sich eine Dezimalzahl, bei der sieben Nachkommastellen mit denen der Kreiszahl übereinstimmen:[A 1] Beispiele zur Veranschaulichung der Fehler:
Konstruktion von Jacob de Gelder 1849 erschien in Grünerts Archiv eine elegante und offensichtlich einfache Konstruktion von Jacob de Gelder (1765–1848). Das war 64 Jahre früher als die Veröffentlichung der vergleichbaren Konstruktion von S. A. Ramanujan im Jahr 1913.[65] Sie beruht auf der Näherung[65] und der Aufteilung des Wertes in die zwei Summanden Der Wert dieses Bruchs hat mit der Kreiszahl bereits sechs Nachkommastellen gemeinsam. Er stammt vom chinesischen Mathematiker Zu Chongzhi aus dem 5. Jahrhundert und wird deshalb auch Zu Chongzhi-Bruch genannt.[66] Jacob de Gelder konstruierte nicht die Seite des Quadrats; es genügte ihm den folgenden Wert zu finden:
Die nebenstehende Abbildung – im Folgenden beschrieben – zeigt die Konstruktion von Jacob de Gelder mit Weiterführung. Zeichne zwei zueinander senkrechte Mittellinien eines Kreises mit Radius CD = 1 und bestimme die Schnittpunkte A und B. Lege die Strecke CE = fest und verbinde E mit A. Bestimme auf AE und ab A die Strecke AF = . Zeichne FG parallel zu CD und verbinde E mit G. Zeichne FH parallel zu EG, dann ist AH = Bestimme BJ = CB und anschließend JK = AH. Halbiere AK in L und ziehen den Thaleskreis um L ab A, dabei ergibt sich der Schnittpunkt M. Die Strecke BM ist die Wurzel aus AK und damit die Seitenlänge a des gesuchten nahezu flächengleichen Quadrates. Beispiele zur Veranschaulichung der Fehler:
Konstruktion von E. W. Hobson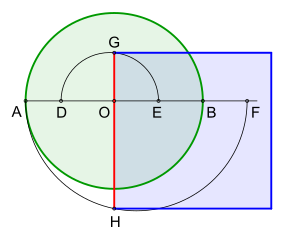 Eine besonders einfache und gut nachvollziehbare Konstruktion stammt von E. W. Hobson aus dem Jahr 1913. Sie benötigt für die Seite des Quadrates nur drei Halbkreise und zwei zueinander rechtwinklig stehende Strecken.[67] Das nebenstehende Bild zeigt die Konstruktion mit eingezeichnetem Kreis und dem gesuchten Quadrat. Vorgaben und Beschreibung:
Zeichne die Halbkreise mit und als Durchmesser. Errichte abschließend die Senkrechte zu durch Die dadurch erzeugten Schnittpunkte und liefern die Seitenlänge des gesuchten Quadrates
Bei einem Kreis mit dem Radius gleichen vier Nachkommastellen der Seitenlänge des Quadrates denen in [67] Beispiel zur Veranschaulichung der Fehler:
Konstruktionen von Srinivasa RamanujanEbenfalls im Jahr 1913 erschien eine Konstruktion des indischen Mathematikers Srinivasa Ramanujan,[68] die ebenfalls auf der Näherung beruht. Ramanujan merkte bezüglich der Genauigkeit seines Verfahrens an, dass bei einer Kreisfläche von 140.000 Quadratmeilen die konstruierte Quadratseite nur um etwa einen Zoll vom wahren Wert abweiche. Beschreibung (Übersetzung):[68]
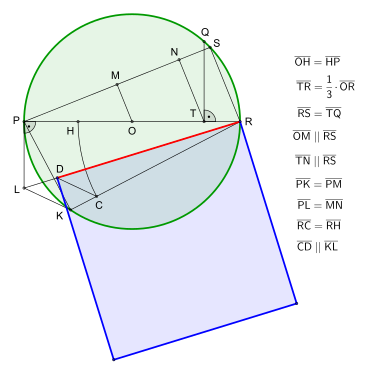
 siehe hierzu die Animation. In einer Arbeit aus dem Folgejahr (1914) lieferte Ramanujan neben anderen Näherungsverfahren eine weitere Quadratur mit Zirkel und Lineal. Dieser liegt der Wert zugrunde, der sogar auf acht Stellen nahekommt.[69] Ramanujan konstruierte in dieser Quadratur nicht die Seitenlänge des gesuchten Quadrates; es genügte ihm, die Strecke OS darzustellen. In der nebenstehenden Weiterführung der Konstruktion wird die Strecke OS zusammen mit der Strecke OB zur Darstellung der mittleren Proportionalen (rote Strecke OE) herangezogen. Beschreibung (Übersetzung):[70]
Weiterführung der Konstruktion bis zur gesuchten Seitenlänge des Quadrates: Beispiele zur Veranschaulichung der Fehler:
Konstruktion von Eduard GregoriEduard Gregori, ein Südtiroler Handelsmann, zeichnete kurz nach dem Zweiten Weltkrieg eine Näherungskonstruktion, die bezüglich Einfachheit, Ästhetik und Genauigkeit bemerkenswert ist. Die Erstveröffentlichung erfolgte im Jahr 1947 von Georg Innerebner in Der Schlern, einer Monatszeitschrift für Südtiroler Landeskunde.[72] Im Jahr 2020 beschrieb und bewies Heinrich Hemme die Konstruktion in der Monatszeitschrift Spektrum der Wissenschaft.[73]  Konstruktionsbeschreibung: Es beginnt mit einem Kreis mit beliebigem Radius um den Mittelpunkt . Anschließend wird das Quadrat so eingezeichnet, dass dessen Seiten Tangenten des Kreises sind. Nach dem Ziehen der beiden Diagonalen und ergibt sich nahe dem Eckpunkt der Schnittpunkt . Der nun folgende Kreisbogen um mit Radius erzeugt den Schnittpunkt auf der Quadratseite . Es geht weiter mit einem kurzen Kreisbogen um mit Radius , der Schnittpunkt ist auf der Quadratseite . Nun bedarf es nur noch der Konstruktion des Punktes auf , dessen Abstand zum Eckpunkt ein Viertel der Strecke beträgt. Die abschließende Parallele zur Quadratseite ab bis zur Diagonalen liefert die Seite des gesuchten Quadrates Bei einem Kreis mit dem Radius gleichen fünf Nachkommastellen der Seitenlänge des Quadrates denen in und somit Beispiele zur Veranschaulichung der Fehler:
Konstruktion von Louis Loynes Eine einfache Methode veröffentlichte Louis Loynes 1961.[74] Sie beruht auf der Feststellung, dass der Flächeninhalt des Umkreises eines rechtwinkligen Dreiecks gleich dem Quadrat über der größeren Kathete ist, wenn der Tangens des kleineren Winkels, also das Verhältnis von kleinerer zu größerer Kathete, beträgt, ein Wert, der sehr nahe an dem Bruch liegt. Daraus ergibt sich eine einfache Näherung, indem man das (konstruierbare) rechtwinklige Dreieck mit dem Katheten-Verhältnis 23:44 zur Quadratur benutzt. Der angenäherte Wert für die Kreiszahl von ist etwas besser als bei Kochańskis Konstruktion. Beispiele zur Veranschaulichung der Fehler:
Näherungslösung mithilfe eines konstruierten BruchsWird auf einem Strahl ein Bruch, dessen Wert annähernd der Kreiszahl entspricht, mithilfe des dritten Strahlensatzes konstruiert, ist es mit mehr oder weniger konstruktivem Aufwand möglich, jede gewünschte Anzahl Nachkommastellen von darzustellen. Für die Ermittlung der Seitenlänge des Quadrates kann z. B. der Bruch herangezogen werden. Als Näherungswert der Kreiszahl liefert er beachtliche fünfzehn gleiche Nachkommastellen. Der Kehrbruch dieses Bruchs stammt von Johann Heinrich Lambert, der ihn u. a. m. bereits 1770 in seinem Buch Beyträge zum Gebrauche der Mathematik und deren Anwendung[75] veröffentlichte. Nicht-klassisches Verfahren mittels QuadratrizesLockert man die Beschränkung auf Zirkel und Lineal und lässt weitere Konstruktionsmittel zu, so erhält man eine Vielzahl von Möglichkeiten, den Kreis zu quadrieren beziehungsweise die Seitenlänge des Quadrates exakt zu konstruieren. Mithilfe spezieller transzendenter Kurven, den sogenannten Quadratrizes, als einzigem zusätzlichem Hilfsmittel, ist es möglich einen Kreis exakt zu quadrieren.[76] Dabei wird im mathematischen Modell die Existenz beziehungsweise Verfügbarkeit einer solchen Quadratrix einfach vorausgesetzt. Zum praktischen Zeichnen auf Papier steht sie zum Beispiel in Form einer Schablone oder eines Plotterausdrucks zur Verfügung, zudem existieren einige spezielle mechanische Zeichengeräte, mit denen sich solche Kurven erzeugen lassen. Zu den ältesten bereits seit der Antike bekannten Quadratrizes, die bei der Kreisquadratur Verwendung finden, gehören z. B. die im Folgenden beschriebenen Kurven Quadratrix des Hippias und die Spirale des Archimedes. Quadratrix des HippiasDas Bild 1 zeigt die Quadratur des Einheitskreises mithilfe der Quadratrix des Hippias, deren Graph durch und verläuft.[77] Nach der Konstruktion der Kreiszahl mit der Quadratrix des Hippias als zusätzliches Hilfsmittel ergibt sich durch Verlängern der Strecke – nach dem Satz des Thales – die Wurzel aus gleich Das eingezeichnete Quadrat mit der Seitenlänge hat exakt den gleichen Flächeninhalt wie der Kreis um
Archimedische SpiraleIm Bild 2 ist die Quadratur des Einheitskreises mithilfe der archimedischen Spirale dargestellt. Deren Windungsabstand beträgt (mit ) . Der Graph der Spirale schneidet die -Achse in und liefert somit die Kreiszahl als Strecke [78] Nun bedarf es nur noch des Projizierens der Kreiszahl auf die -Achse und der Konstruktion der Wurzel Das abschließend eingezeichnete Quadrat mit der Seitenlänge hat exakt den gleichen Flächeninhalt wie der Kreis um SinuskurveDas Bild 3 zeigt die Quadratur des Einheitskreises mithilfe des Graphen der Funktion , allgemein bekannt als „Sinuskurve“.[79] Die Sinuskurve verläuft durch den Mittelpunkt des Einheitskreises und schneidet in die Achse. Die Seitenlänge des gesuchten Quadrats, dessen Flächeninhalt gleich dem des Einheitskreises ist, erhält man elementar mittels des Thaleskreises über und der errichteten Senkrechten zu in mit Schnittpunkt im Thaleskreis. Die Halbierung von in liefert mit den Inkreisradius des gesuchten Quadrats .
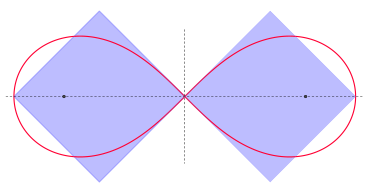
VariantenTarskis Problem der Quadratur des KreisesAlfred Tarski stellte 1925 die Aufgabe, einen Kreis in beliebig viele Teile zu stückeln und diese dann durch reine Bewegung (also ohne Streckung) so zu verschieben, dass ein Quadrat entsteht.[80] Miklós Laczkovich publizierte 1990 eine Lösung: Er bewies, dass es möglich ist, einen Kreis in endlich viele Teile zu zerlegen und diese nur durch Bewegung so zu verschieben, dass ein Quadrat entsteht.[81] Er zerteilte den Kreis in 1050 Stücke. Für den Beweis benötigt er jedoch das Auswahlaxiom, das von den meisten Wissenschaftlern heute zwar akzeptiert wird, aber nicht selbstverständlich ist. Der Beweis ähnelt stark dem Banach-Tarski-Paradoxon. Laczkovich hat zwar bewiesen, dass (unter Annahme des Auswahlaxioms) so eine Zerlegung existiert, diese Zerlegung lässt sich jedoch nicht explizit angeben.[80] LemniskateIm Gegensatz zum Kreis ist es möglich, zu einer Lemniskate (∞) zwei Quadrate zu konstruieren, welche die gleiche Fläche einspannen. Deren Seitenlängen entsprechen dem größten Lemniskatenradius a.[82] Quadratur einer von Kreisbögen begrenzten FlächeObwohl die Quadratur eines Vollkreises nicht möglich ist, gibt es neben den oben erwähnten Möndchen des Hippokrates auch andere von Kreisbögen begrenzte Flächen, die man sehr wohl quadrieren kann. Die Abbildungen zeigen die Längsschnittsfläche eines vasenähnlichen Körpers mit der zugehörigen Quadratur und veranschaulichen die Konstruktion. Der untere Teil der Vasenfigur wird von einem Dreiviertelkreis und der obere Teil von drei Viertelkreisen umrandet. Alle Kreisbögen sind ohne Beschränkung der Allgemeinheit jeweils Teil eines Einheitskreises.[83]
Siehe auch
Literatur und QuellenAllgemein
Zur Transzendenz von π
Unterhaltungsmathematik
WeblinksWikiversity: Eine Vorlesung zur Quadratur des Kreises – Kursmaterialien
Commons: Quadratur des Kreises – Sammlung von Bildern
Wiktionary: Quadratur des Kreises – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Wiktionary: Quadratur – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Wikibooks: Die Quadratur des Kreises – Lern- und Lehrmaterialien
… mit 245850922 78256779, dem Kehrwert eines Bruchs von Johann Heinrich Lambert Anmerkungen
Einzelnachweise
|
Portal di Ensiklopedia Dunia















































![{\displaystyle {\overline {GH}}=r\cdot 1{,}772\;4{\color {red}67\ldots }\;[LE].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a641293958c9de4abf007142fa9b8c83ff296e2b)

![{\displaystyle r=1\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/937d14de992ab8b056dbf1bb468ed1cb35d25554)















![{\displaystyle \pi \approx {\sqrt[{4}]{9^{2}+{\frac {19^{2}}{22}}}}=3{,}141\;592\;65{\color {red}2\;\ldots }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e27f9050a3048e77bc0bf9a7265a2f41deedc02)















![{\displaystyle {\overline {HK}}=r\cdot 1{,}772\;45{\color {red}5\ldots }\;[LE].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65100214a607a2f6b1ba53237ab8a58428b214b2)