|
Quadratur des Quadrates Unter der Quadratur des Quadrates versteht man die lückenlose und überlappungsfreie Bedeckung („Parkettierung“) eines gegebenen Quadrates mit kleineren Quadraten, deren Seitenlängen ganzzahlige Werte haben. Die Bezeichnung Quadratur des Quadrates wurde in scherzhafter Anlehnung an die Quadratur des Kreises gewählt,[1] obwohl die beiden Problemstellungen nichts miteinander zu tun haben. Eigenschaften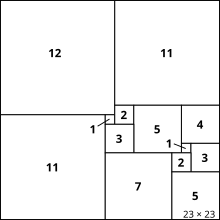  SeitenlängenDer deutsche Geometer Max Dehn bewies 1903, dass die Seiten eines mit Quadraten parkettierten Rechteckes (also auch die eines Quadrates) mit den Seiten der Teilquadrate kommensurabel sein müssen. Dies bedeutet, dass die Seitenlängen des quadrierten Rechtecks und die aller Teilquadrate ganzzahlige Vielfache einer einzigen Zahl sind; bei geeigneter Wahl der Längeneinheit sind dann alle Seitenlängen ganze Zahlen.[2] OrdnungAls Ordnung (engl. order) einer Parkettierung bezeichnet man die Zahl der Teilquadrate.[3] ZusatzbedingungenTriviale Beispiele für die Parkettierung von und mit Quadraten finden sich in vielen Dingen des Alltags – wie etwa dem Schachbrett oder an jeder mit quadratischen Kacheln gefliesten Küchenwand. Interessant und anspruchsvoll wird die Aufgabenstellung durch folgende Zusatzbedingungen:
Für unperfekte Parkettierungen, also solche, die mehrere kongruente Teilquadrate enthalten, werden weitere Zusatzbedingungen betrachtet:[1][4]
Es ist evident, dass die No-touch-Varianten eine Teilmenge der Nowhere-neat-Parkettierungen sind. BeispieleAbbildung 1 zeigt die perfekte und zugleich einfache Parkettierung geringster Ordnung (21), Abbildung 2 die einfache, unperfekte Quadratur der geringstmöglichen[5] Ordnung 13 (sie ist zugleich vom Typ no touch tiling, da die jeweils gleich großen Teilquadrate einander nicht berühren), Abbildung 3 eine perfekte, aber zusammengesetzte Quadratur der Ordnung 24 (die grau unterlegten Kacheln oben rechts fügen sich zu einem Rechteck zusammen). Mrs. Perkins’s Quilt Als „Mrs. Perkins’s Quilt“ wird die Zerlegung eines gegebenen Quadrates in die kleinstmögliche Anzahl von Teilquadraten bezeichnet, ohne dass diese Quadratur perfekt oder einfach zu sein hat. Die Bezeichnung geht zurück auf eine Rätselaufgabe, die der amerikanische Rätselautor Samuel Loyd 1907 und der britische Unterhaltungsmathematiker Ernest Dudeney 1917 publizierten.[5] In dieser Aufgabe soll ein aus 169 (13 × 13) gleich großen Quadraten zusammengefügter quadratischer Quilt entlang der Nähte in eine möglichst kleine Anzahl von quadratischen Stücken zerschnitten werden. Die Lösung (s. Bild) hat die Ordnung 11; da zwei kongruente Teilstücke (die beiden gelben am oberen Rand) mit einer ganzen Quadratseite aneinandergrenzen, ist sie weder einfach (die beiden Quadrate bilden ein Rechteck) noch perfekt, noch hat sie die Eigenschaften nowhere-neat oder gar no touch. Geschichte Es mag überraschen, dass die Erforschung des eher elementar und einfach anmutenden Problems der Quadratur des Quadrates erst auf das letzte Jahrhundert zurückgeht. Seitdem wurden mehrere Millionen Quadraturen unterschiedlicher Typen und Ordnung entdeckt und dokumentiert, wobei der Ausgangspunkt dieser Entwicklung zunächst die Suche nach der Parkettierung von Rechtecken (nicht zu verwechseln mit der Quadratur des Rechtecks) war. Beispielhaft seien hier einige Meilensteine dieser Entdeckungsgeschichte genannt.[3]
Die perfekte Parkettierung eines Rechtecks mit Quadraten erfolgte schon 1925 durch den polnischen Mathematiker Zbigniew Morón. 2008 gelang Frederick und James Henle die lückenlose Zerlegung der Ebene mit Quadraten der Seitenlängen 1, 2, 3, 4 und so weiter.[9] 1993 fand S. J. Chapman eine Zerlegung eines Möbiusbandes mit fünf Quadraten unterschiedlicher Größe. Für einen Zylinder benötigt man mindestens neun Quadrate.[10] Einzelnachweise(Quellen siehe Literatur und Weblinks.)
Literatur
WeblinksCommons: Quadratur des Quadrates – Sammlung von Bildern
|
Portal di Ensiklopedia Dunia