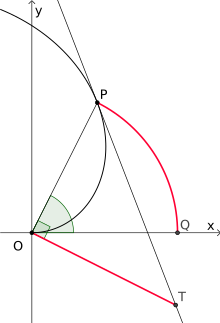
Archimedische Spirale
|
Read other articles:

Evan McMullinMcMullin pada 2016LahirDavid Evan McMullin2 April 1976 (umur 48)Provo, Utah, Amerika SerikatPendidikanUniversitas Brigham Young (Sarjana)Universitas Pennsylvania(Magistrat)Partai politikIndependen (2016–kini)Partai Republik (sebelum 2016)Situs webSitus web resmi David Evan McMullin[1] (lahir 2 April 1976) adalah seorang aktivis politik Amerika Serikat dan mantan pejabat operasi Central Intelligence Agency (CIA) yang maju sebagai seorang independen pada pemilihan umum …

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддійсь…

Histidina Nama sistematik Asam S-2-amino-3-(3H-imidazol-4-il)propanoat Singkatan HisH Kode genetik CAU CAC Rumus kimia C6H9N3O2 Massa molekul 155,16 g mol-1 Titik lebur 287 °C Massa jenis ? g cm-3 Titik isoelektrik 7,59 pKa 1,706,049,09 Nomor CAS L [71-00-1] SMILES C1=C(NC=N1)CC(C(=O)O)N Histidina merupakan satu dari 20 asam amino dasar yang ada dalam protein. Bagi manusia histidina merupakan asam amino yang esensial bagi anak-anak. Rantai samping imidazol dan nilai pKa yang relatif netral…

جزء من سلسلة مقالات حولالنحو والتصريف في العربية الإعراب الكلمة الاسم الفعل الحرف العبارات الجملة الاسمية جملة اسمية مختصرة الفعلية الجملة الفعلية الواقعة مضافا إليه شبه الجملة النوع المُعرب المبني الوقوف المجرد المزيد أقسام الإعراب إعراب ظاهر (لفظي) إعراب تقديري إعراب م�…

Politics of Portugal Constitution Executive President (list) Marcelo Rebelo de Sousa Prime Minister (list) Luís Montenegro Cabinet Legislature Assembly of the Republic President: Augusto Santos Silva Judiciary Constitutional Court Supreme Court of Justice Court of Auditors Supreme Administrative Court Elections Recent elections Presidential: 201620212026 Legislative:201920222024 Local: 201320172021 European: 201420192024 Political parties Politicians Administrative divisions Districts Autonomou…

Voce principale: Associazione Calcio Ancona. Ancona CalcioStagione 1999-2000Sport calcio Squadra Ancona Allenatore Fabio Brini Presidente Mario Bonsignore Serie C12º nel girone B. Promosso in B Coppa Italia2º nel girone L Maggiori presenzeCampionato: Storari (33) Miglior marcatoreCampionato: La Grotteria (9) StadioStadio del Conero 1998-1999 2000-2001 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Ancona Calcio nelle competizioni ufficiali della…

Crowley'sIndustryDepartment storeFounded1909Defunct1999Fateliquidated; sold to Value CitySuccessorValue CityHeadquartersDetroit, MichiganUnited StatesKey peopleJoseph, William, and Daniel CrowleyNumber of employees1,300ParentCrowley Milner and CompanySubsidiariesSteinbach's Crowley Milner and Company, generally referred to as Crowley's, was a department store chain founded in Detroit, Michigan, in 1909. After several years of financial difficulties, the company ceased operation in 1999 and its a…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Fosil Pandu yaitu fosil punya ciri-ciri khusus yang ada dalam lapisan bumi.&#…

Book by Anwar Shah Kashmiri Al-Arf al-Shadhi sharh Sunan al-Tirmidhi Arabic coverEditorMuhammad Chiragh PunjabiAuthorAnwar Shah KashmiriOriginal titleالعرف الشذي شرح سنن الترمذيLanguageArabicSubjectSunan al-TirmidhiGenreCommentaryPublished1919Publication placeBritish IndiaMedia typePrintISBN9789957674991 Turath PublishingOCLC884580861Dewey Decimal297.125 Al-Arf al-Shadhi sharh Sunan al-Tirmidhi (Arabic: العرف الشذي شرح سنن الترمذي, romanize…

MTV Movie & TV AwardsMTV Movie & TV Awards LuogoStati Uniti d'America Anni1992 - oggi Frequenzaannuale Generecinema e televisione OrganizzazioneMTV Sito ufficialewww.mtv.com/movie-and-tv-awards Modifica dati su Wikidata · Manuale Gli MTV Movie & TV Awards, in precedenza chiamato MTV Movie Awards,[1] sono uno spettacolo di premiazione cinematografica presentato annualmente su MTV e che contiene anche parodie di alto livello, cui collaborano diverse celebrità. Le nominat…
La Morandière-Rochebaucourt Le pont de l'Arche-de-Noé, situé à Rochebaucourt. Administration Pays Canada Province Québec Région Abitibi-Témiscamingue Subdivision régionale Abitibi Statut municipal Municipalité Maire Mandat Alain Trudel 2023-2025 Code postal J0Y 2J0 Constitution 1er janvier 2023 Démographie Population 350 hab. (2023) Densité 0,57 hab./km2 Géographie Coordonnées 48° 36′ 57″ nord, 77° 38′ 15″ ouest Superficie 61 02…

1982 video game For other uses, see Pole Position (disambiguation). 1982 video gamePole PositionArcade flyerDeveloper(s)NamcoPublisher(s)JP/EU: Namco[2]NA/FRA: Atari, Inc.[1]Designer(s)Kazunori SawanoSho OsugiShinichiro OkamotoProgrammer(s)Koichi TashiroComposer(s)Nobuyuki OhnogiYuriko KeinoPlatform(s)Arcade, Atari 2600, Atari 5200, Atari 8-bit, Commodore 64, TI-99/4A, VIC-20, Vectrex, Mobile phoneReleaseJP: September 16, 1982NA: November 30, 1982EU: Late 1982Genre(s)RacingMode(s…

貂属化石时期:中新世至現在 PreЄ Є O S D C P T J K Pg N 紫貂 科学分类 界: 动物界 Animalia 门: 脊索动物门 Chordata 纲: 哺乳纲 Mammalia 目: 食肉目 Carnivora 科: 鼬科 Mustelidae 亚科: 貂熊亞科 Guloninae 族: 貂族 Martini 属: 貂属 MartesPinel, 1792 種 另见内文 分布範圍: M. americana + caurina = 青色和藍綠色 M. flavigula = 深藍色和棕褐色 M. foina = 銹色、棕色和棕褐色 M. gwatkinsii M. martes = 橙色, �…

Denver NuggetsStagione 1993-1994Sport pallacanestro Squadra Denver Nuggets AllenatoreDan Issel Vice-allenatoriGene Littles, Mike Evans NBA42-40 (.512)Division: 4º posto (Midwest)Conference: 8º posto (Western) PlayoffSemifinali Western Conference (perso 3-4 contro Utah) StadioMcNichols Sports Arena 1992-1993 1994-1995 La stagione 1993-94 dei Denver Nuggets fu la 18ª nella NBA per la franchigia. I Denver Nuggets arrivarono quarti nella Midwest Division della Western Conference con un recor…

US quasi-autonomous non-governmental organization Not to be confused with the Great Society National Endowments for Arts and Humanities programs. This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: National Endowment for Democracy – news · newspapers · books · scholar · JSTOR (February 2023) (Learn how and when to remove this message) National Endowment for De…

Type of closed research institutions in the Soviet Union For other uses, see OKB (disambiguation). Sukhoi Company (JSC) head office/Sukhoi OKB OKB is a transliteration of the Russian initials of опытно-конструкторское бюро – opytno konstruktorskoye byuro, meaning 'experiment and design bureau'. During the Soviet era, OKBs were closed institutions working on design and prototyping of advanced technology, usually for military applications. The corresponding English langu…

Mil Mi-24D Hind Un Mil Mi-24D de l’Armée russe en 2018. Rôle Hélicoptère tactique armé Constructeur / Mil Premier vol 19 septembre 1969 Mise en service 1972 Date de retrait Toujours en service Nombre construit + de 2 500 exemplaires Équipage 2/3 + 8 soldats Motorisation Moteur Klimov TV3-117 Nombre 2 Type Turbomoteurs Puissance unitaire 2 200 ch Nombre de pales 5 Dimensions Diamètre du rotor 17,30 m Longueur 17,51 m Hauteur 4,25 m Masses À vide 6 …

North American Indigenous peoples within the boundaries of present-day Canada Native Canadian redirects here. For Canadian people in general, see Canadians. Ethnic group Indigenous peoples in CanadaPeuples autochtones au CanadaIndigenous peoples in Canada and the U.S., % of population by areaTotal population1,807,2505.0% of the Canadian population (2021)[1]LanguagesIndigenous languages, Indigenous English, Canadian English and Canadian FrenchReligionChristianity (mainly Roman Cathol…

نوبيرن الإحداثيات 32°35′41″N 87°32′08″W / 32.594818°N 87.535431°W / 32.594818; -87.535431 [1] تاريخ التأسيس 1854 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة هيل خصائص جغرافية المساحة 3.017242 كيلومتر مربع (1 أبريل 2010)[3] ارتفاع 57 متر عدد …

魔法ワールド > ハリー・ポッター (映画シリーズ) > ハリー・ポッターと炎のゴブレット (映画) ハリー・ポッターと炎のゴブレット Harry Potter And The Goblet Of Fire監督 マイク・ニューウェル脚本 スティーブ・クローブス原作 J・K・ローリング製作 デヴィッド・ハイマン製作総指揮 デヴィッド・バロンターニャ・セガーチェン出演者 ダニエル・ラドクリフルパート�…









![{\displaystyle {\frac {a}{2}}\left[\varphi \,{\sqrt {1+\varphi ^{2}}}+\ln \left(\varphi +{\sqrt {1+\varphi ^{2}}}\right)\right]_{\varphi _{1}}^{\varphi _{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddf8d5e1cc73e66c0fd656c90d457db98defa2f3)
![{\displaystyle {\frac {a}{2}}\left[\varphi \,{\sqrt {1+\varphi ^{2}}}+\operatorname {arsinh} \varphi \right]_{\varphi _{1}}^{\varphi _{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17e6fd40fc450d8e32c533b8054cbf00c4ac8fb8)


![{\displaystyle {\frac {a}{2}}\left[\varphi \,{\sqrt {1+\varphi ^{2}}}+\ln \left(\varphi +{\sqrt {1+\varphi ^{2}}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f46d4800b7f28600abec47c8a3509519a235ef6)