测圆海镜

知不足斋丛书《测圆海镜》圆城图式，其中用天地乾坤等指代三角形内各点

《测圆海镜》是中国金代数学家李冶的代表作，于公元1248年写成。全书一共十二卷，由一百七十个问题组成。书中对勾股容圆的问题进行了探讨，系统地建立了“天元术”（列一元方程的方法）来解决几何问题。《测圆海镜》被认为是中国现存的第一部天元术著作。 天元术是对具体问题列出方程而后求解的方法。天元术于宋金时期开始发展，到元朝达到一个高峰。在《测圆海镜》问世之前，中国虽有以天人代表未知数用以布列方程和多项式的工作，但早期著作已失，仅存被引用的一些片段。李冶在《测圆海镜》中系统而概括地总结了天元术，用“天元”代替未知数，列出方程，然后求解。

内容

《测圆海镜》由卷一的圆城图式、说明各个长度名称的总率名号、给出各个长度数值的今问正数、囊括了各个量之间关系的公式总集识别杂记；卷二至卷十二，共一百七十个问题及其解答所组成。书中一共有148问，182种方法是以天元术列出方程以求解，其中列出一次方程31个，二次方程106个，三次方程24个，四次方程20个，六次方程1个[1]

卷一

圆城图式

圆城图式（右图）是全书的总括图解，由一个直角三角形（古时称为勾股形）、它的内切圆以及一些特定的点和直线组成。其中的顶点、圆心和交点都用某个汉字来指代。最大的三角形的三个顶点分别是天、地、乾，天地乾三角形的内切圆圆心称为心。过心的垂直线从上至下分别和三角形、内切圆交于日、南、北三点。过心的水平线从左至右分别和三角形、内切圆交于川、东、西三点。过东的垂直线和过南的水平线都是内切圆的切线，它们分别交天地乾三角形于艮、坤、山、月四点，而相交于巽点。乾坤巽艮构成一个正方形。过月的垂直线交东西水平线于青点，交地乾边于泉点。过山的水平线交南北垂直线于朱点，交天乾边于金点。而这两条线相交于泛点。最后过日的水平线交天乾边于旦点，过川的垂直线交地乾边于夕点。总共22个点。

总率名号

全书所研究的三角形一共有15个，全部是以天地线之间的线段为弦（斜边）的直角三角形。总率名号给出了这些三角形和线段的名称。它们分别是：

序号	三角形名称	对应的三个顶点	弦0c	股0b	勾0a
1	通	天地乾	通弦（天地）	通股（天乾）	通勾（地乾）
2	边	天西川	边弦（天川）	边股（天西）	边勾（西川）
3	底	日地北	底弦（日地）	底股（日北）	底勾（地北）
4	黄广	天山金	黄广弦（天山）	黄广股（天金）	黄广勾（山金）
5	黄长	月地泉	黄长弦（月地）	黄长股（月泉）	黄长勾（地泉）
6	上高	天日旦	上高弦（天日）	上高股（天旦）	上高勾（日旦）
7	下高	日山朱	下高弦（日山）	下高股（日朱）	下高勾（山朱）
8	上平	月川青	上平弦（月川）	上平股（月青）	上平勾（川青）
9	下平	川地夕	下平弦（川地）	下平股（川夕）	下平勾（地夕）
10	大差	天月坤	大差弦（天月）	大差股（天坤）	大差勾（月坤）
11	小差	山地艮	小差弦（山地）	小差股（山艮）	小差勾（地艮）
12	皇极	日川心	皇极弦（日川）	皇极股（日心）	皇极勾（川心）
13	太虚	月山泛	太虚弦（月山）	太虚股（月泛）	太虚勾（山泛）
14	明	日月南	明弦（日月）	明股（日南）	明勾（月南）
15	叀	山川东	叀弦（山川）	叀股（山东）	叀勾（川东）

其中弦是三角形斜边，股是三角形的长直角边（这里是竖直的），勾是三角形短直角边（这里是水平的）。（${\displaystyle a_{1}}$代表通勾，${\displaystyle b_{1}}$代表通股，${\displaystyle c_{1}}$代表通弦，余类推）。

今问正数

今问正数一节给出了圆城图式中每个线段的长度。其中以内切圆的半径为120步，作为标准。

• 弦
• 勾
• 股
• 勾股和：a + b
• 勾股校：b - a
• 勾弦和：a + c
• 勾弦校：c - a
• 股弦和：b + c
• 股弦校：c - b
• 弦校和：c + (b - a)
• 弦校校：c - (b - a)
• 弦和和：(a + b) + c
• 弦和校：(a + b) - c

例子:「通弦六百八十，勾三百二十，股六百；勾股和九百二十，较（兩者的差）二百八十；勾弦和一千，较三百六十；股弦和一千二百八十，较八十；弦较和九百六十，较四百；弦和和一千六百，较二百四十。」

15个勾股形中上高 = 下高；上平 = 下平，因此，15个勾股形中，只有13个勾股形是相异的。

《今问正数》共15个勾股形×13项=195项[2]。 ，列表如下。

识别杂记

识别杂记都是关于不同线段之间的几何关系式。一共给出了692个公式。是全书的纲领。

识别杂记包含八项：

• 诸杂名目：是全书的总纲，列出各项定义，例如虚勾虚股相得名为虚率，高股平勾差名为角差，又名远差等等。诸杂名目中还列出三十余项定理，如凡大差小差相乘为半段径幂，大差勾小差股相乘同上、黄广股黄长勾相乘为经幂等等。

名目

名目	定义
内率	${\displaystyle a_{14}*b_{15}}$
外率	${\displaystyle b_{14}*a_{15}}$
虚率	${\displaystyle a_{13}*b_{13}}$
角差	${\displaystyle b_{7}-a_{8}}$
次差	${\displaystyle (b_{14}-a_{14})+(b_{15}-a_{15})}$
混同和	${\displaystyle b_{11}+a_{10}}$
傍差	${\displaystyle (b_{14}-a_{14})-(b_{15}-a_{15})}$
夎差	${\displaystyle (b_{14}-a_{14})-(b_{15}-a_{15})-(b_{13}-a_{13})}$
夎和	${\displaystyle (b_{14}-a_{14})-(b_{15}-a_{15})-(b_{13}+a_{13})}$

杂用公式

[3]

1. ${\displaystyle (c_{1}-a_{1})*(c_{1}*b_{1})}$= ${\displaystyle 1 \over 2}$*${\displaystyle (d_{1})^{2}}$
2. ${\displaystyle a_{10}*b_{11}}$= ${\displaystyle 1 \over 2}$${\displaystyle (d_{1})^{2}}$
3. ${\displaystyle a_{13}*b_{1}}$= ${\displaystyle 1 \over 2}$${\displaystyle (d_{1})^{2}}$
4. ${\displaystyle a_{1}*b_{13}}$= ${\displaystyle 1 \over 2}$${\displaystyle (d_{1})^{2}}$
5. ${\displaystyle b_{2}*b_{15}}$= ${\displaystyle }$${\displaystyle (r_{1})^{2}}$
6. ${\displaystyle a_{14}*a_{3}}$= ${\displaystyle (r_{1})^{2}}$
7. ${\displaystyle a_{5}*b_{4}}$= ${\displaystyle (d_{1})^{2}}$
8. ${\displaystyle a_{8}*b_{6}}$= ${\displaystyle a_{9}*b_{7}}$${\displaystyle =(r_{1})^{2}}$
9. ${\displaystyle (b_{14}*c_{14})*(a_{15}+c_{15})}$= ${\displaystyle (r_{1})^{2}}$
10. ${\displaystyle c_{6}*c_{8}}$= ${\displaystyle c_{7}*c_{9})}$=${\displaystyle a_{13}*b_{13}}$
11. ${\displaystyle }$

五和五较

1. ${\displaystyle a_{2}+b_{2}+c_{2}=b_{1}+c_{1}}$[4]
2. ${\displaystyle a_{3}+b_{3}+c_{3}=a_{1}+c_{1}}$
3. ${\displaystyle a_{4}+b_{4}+c_{4}=2b_{1}}$
4. ${\displaystyle a_{5}+b_{5}+c_{5}=2a_{1}}$
5. ${\displaystyle a_{6}+b_{6}+c_{6}=b_{1}}$
6. ${\displaystyle a_{7}+b_{7}+c_{7}=b_{1}}$
7. ${\displaystyle a_{8}+b_{8}+c_{8}=a_{1}}$
8. ${\displaystyle a_{9}+b_{9}+c_{9}=a_{1}}$
9. ${\displaystyle a_{10}+b_{10}+c_{10}=b_{1}+c_{1}-a_{1}}$
10. ${\displaystyle a_{11}+b_{11}+c_{11}=c_{1}-b_{1}+a_{1}}$
11. ${\displaystyle a_{12}+b_{12}+c_{12}=c_{1}}$
12. ${\displaystyle a_{13}+b_{13}+c_{13}=a_{1}+b_{1}-c_{1}}$
13. ${\displaystyle a_{14}+b_{14}+c_{14}=c_{1}-a_{1}}$
14. ${\displaystyle a_{15}+b_{15}+c_{15}=c_{1}-c_{1}}$

此外还有诸弦，大小差，诸差，诸率互见，四位拾遗，拾遗。

一共692关系式，这些关系式完全是几何定理，与具体数值无关。

举例：第三条中“勾股和即弦黄和”一句就是：三角形两直角边之和等于斜边加上内切圆直径（“黄”指内切圆直径）。这个命题可以由直角三角形的勾股定理推出：

设直角三角形三边分别为${\displaystyle a}$、${\displaystyle b}$、${\displaystyle c}$，其中${\displaystyle a^{2}+b^{2}=c^{2}}$

内接圆直径${\displaystyle d={\frac {2ab}{a+b+c}}}$，因此

内接圆直径 + 斜边 = ${\displaystyle d+c={\frac {2ab}{a+b+c}}+c={\frac {2ab+c^{2}+ac+bc}{a+b+c}}}$

${\displaystyle ={\frac {2ab+a^{2}+b^{2}+ac+bc}{a+b+c}}={\frac {(a+b)(a+b+c)}{a+b+c}}}$

${\displaystyle =a+b}$ = 两直角边之和

后面出现的各问题，都根据这些公式中的相等关系而列出方程，然后求解。

李冶的692个公式中，有8个是错误的，只是因为数值吻合而被误认为成立。

新设第一率

新设第二率

新设第三率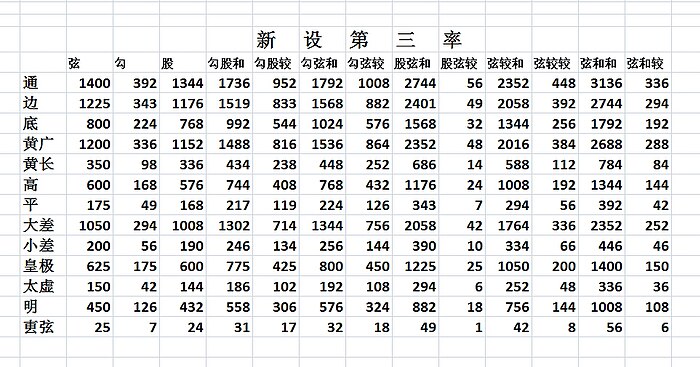

新设第四率

第二卷

正率14问

测圆海镜卷二 正率

从第二卷开始，《测圆海镜》中一共出现了一百七十个问题，它们都是围绕着同一个题设背景而展开。 在第二卷开头，李冶作出了以后题目公用的总假设：

假令圆城一所，不知周径，四面开门，门外纵横各有十字大道。其西北十字道头定为乾地，其东北十字道头定为艮地，其东南十字道头定为巽地，其西南十字道头定为坤地。所有测望杂法，一一设问如后。

这里的圆城就是指天地乾三角形的内切圆，其方向按照圆城图式里面东南西北四个点的位置而定（注意北在下方，东在左边，与现在通用的方位相反），所谓的“乾地”、“坤地”则是指圆城图式里面出现的乾点、坤点等等。以后的每个问题中要求的长度都是圆城的半径或直径。

接下来的问题都是已知某些线段的长度，问圆城的半径或直径。李冶在每一题的题目之后都先写出解法（代数演算），再给出演草（代入数值的计算）。

洞渊九容

开头十个问题，不需要天元方程。清代数学李善兰认为，第一个问题和《九章算术》的勾股容圆题目一样，第二问至第十问就是《自序》中提到的“洞渊九容”[5]。但李冶原书或《四库全书》李锐较本都没有这九个问题的细草，李善兰在《天算或问》一书中根据相似三角形原理求得各式，并以第二问为例阐明如下[6]：

${\displaystyle {a_{1} \over a_{1}+b_{1}+c_{1}}={a_{2} \over a_{2}+b_{2}+c_{2}}}$

${\displaystyle {b_{1} \over b_{1}+c_{1}}={a_{2} \over b_{2}+c_{2}}}$

又因：

${\displaystyle b_{1}+c_{1}=a_{2}+b_{2}+c_{2}}$

所以

${\displaystyle {2b_{1}c_{1} \over a_{1}+b_{1}+c_{1}}={2b_{2}c_{2} \over b_{2}+c_{2}}}$

得

${\displaystyle {2a_{2}\times b_{2} \over a_{2}+b_{2}+c_{2}}=d}$

其余类推。 。

第一问：或问：甲乙二人俱在乾地，乙东行三百二十步而立。甲南行六百步望见乙，问径几里？

答曰：城径二百四十步。

勾股容圆${\displaystyle d={2a_{1}\times b_{1} \over a_{1}+b_{1}+c_{1}}}$

${\displaystyle ={2*320*600 \over 320+600+{\sqrt {(}}320^{2}+600^{2})}=240}$

第二问：勾上容圆

${\displaystyle {2a_{2}\times b_{2} \over a_{2}+b_{2}+c_{2}}=d}$

第三问：股上容圆

${\displaystyle {2a_{3}\times b_{3} \over a_{3}+b_{3}+c_{3}}=d}$

第四问：勾股上容圆

${\displaystyle {2a_{12}\times b_{12} \over c_{12}}=d}$

第五问：弦上容圆

${\displaystyle {2a\times b \over a+b}=d}$

第六问：勾外容圆

${\displaystyle {2a_{10}\times b_{10} \over b_{10}-a_{10}+c_{10}}=d}$

第七问：股外容圆

${\displaystyle {2a_{11}\times b_{11} \over b_{11}-a_{11}+c_{11}}=d}$

第八问：弦外容圆

${\displaystyle {2a_{13}\times b_{13} \over b_{13}+a_{13}-c_{13}}=d}$

第九问：勾外容圆半

${\displaystyle {2a_{14}\times b_{14} \over c_{14}-a_{14}}=d}$

第十问：股外容圆半

${\displaystyle {2a_{15}\times b_{15} \over c_{15}-b_{15}}=d}$

天元术

测圆海镜细草 卷二 第十四问 草曰

从第十四题开始，引入天元术，将所求的未知量设为“天元”，然后根据识别杂记中给出的公式构造出两个天元式，另其相等，然后解方程得出答案。《测圆海镜》中天元式的次序，高次幂在常数项之上，和《益古演段》，《四元玉鉴》的相反。

第十四问

“或问出西门南行四百八十步有树，出北门东行二百步见之。问答同前”。

法曰：以二行步相乘为实，二行步相并为从，一步常法，得半径。

草曰：立天元一为半径，置南行步在地，

内减天元半径得股圆差：${\displaystyle 480-x}$

元

。

又置乙东行步在地，内减天元，得勾圆差：${\displaystyle 200-x}$

元

以勾圆差增乘股圆差得半段黄方幂：${\displaystyle x^{2}-680x+96000}$

元

又置天元幂以倍之，也为半段黄方幂；

元

因此，得${\displaystyle x^{2}-680x+96000=2x^{2}}$

相消得：${\displaystyle -x^{2}-680x+96000=0}$

元

解方程，得半径${\displaystyle r=120}$。

第三卷

边股17问 [7]

标题文字	已知	未知数x	方程
1	<${\displaystyle b_{2}}$，${\displaystyle c_{4}}$		直接计算
2	${\displaystyle b_{2}}$，${\displaystyle a_{11}}$	d	${\displaystyle x^{2}+a_{11}x-2b_{2}a_{11}=0}$
3	${\displaystyle b_{2}}$，${\displaystyle b_{11}}$	r	${\displaystyle x^{2}+b_{2}x-b_{2}b_{11}=0}$
4	${\displaystyle b_{2}}$，${\displaystyle a_{15}}$	d	${\displaystyle x^{3}+a_{15}x^{2}-4a_{15}b_{2}^{2}=0}$
5	${\displaystyle b_{2}}$，${\displaystyle a_{14}}$	d	${\displaystyle x^{3}-(b_{2}-2a_{14})x^{2}+a_{14}^{2}*x+a_{14}^{2}*b_{2}=0}$
6	${\displaystyle b_{2}}$，${\displaystyle a_{10}}$	r	${\displaystyle x^{2}+(b_{2}-(b_{2}-c_{10}))x+b_{2}(b_{2}-c_{10})=0}$
7	${\displaystyle b_{2}}$，${\displaystyle c_{2}}$	r	${\displaystyle ((1/2)*c_{2}-(1/2)*b_{2}+b_{2})*x^{2}-(1/2)*(c_{2}-b_{2})b_{2}^{2}=0}$
8	${\displaystyle b_{2}}$， ${\displaystyle c_{1}}$	r	${\displaystyle 2x^{2}+((c_{1}+b_{2})+(c_{1}-b_{2}))x-((c_{1}+b_{2})(c_{1}-b_{2})-(c_{1}-b_{2})^{2}))=0}$
9	${\displaystyle b_{2}}$，${\displaystyle c_{6}}$	r	${\displaystyle 2x^{2}-2(b_{2}-2(b_{2}-c_{5}))b_{2}=0}$
10	${\displaystyle b_{2}}$，${\displaystyle b_{14}}$	r	${\displaystyle x^{2}-2b_{2}x+((b_{2}-b_{14})^{2}-b_{14}^{2}=0}$
11	${\displaystyle b_{2}}$，${\displaystyle a_{10}}$	r	${\displaystyle (2b_{2}-a_{10})x-b_{2}a_{10}=0}$
12	${\displaystyle b_{2}}$，${\displaystyle c_{15}}$	${\displaystyle b_{15}}$	${\displaystyle x^{2}+(b_{2}+c_{15})x-b_{2}c_{15}=0}$
13	${\displaystyle b_{2}}$，${\displaystyle c_{14}}$	${\displaystyle a_{14}}$	${\displaystyle x^{4}-2(b_{2}-c_{14})x^{3}+(b_{2}-c_{14})^{2}x^{2}+2b_{2}c_{14}^{2}x-(2(b_{2}-c_{14})-b_{2}))b_{2}c_{14}^{2}=0}$
14	${\displaystyle b_{2}}$，${\displaystyle c_{6}}$		${\displaystyle r={\sqrt {(}}(2c_{6}-b_{2})b_{2})}$
15	${\displaystyle b_{2}}$，${\displaystyle c_{8}}$	r	${\displaystyle -x^{3}-c_{8}x^{2}-b_{2}^{2}x+c_{8}b_{2}^{2}=0}$
16	${\displaystyle b_{2}}$，${\displaystyle b_{14}+c_{14}}$		用洞渊九容公式计算
17	${\displaystyle b_{2}}$，${\displaystyle a_{15}+c_{15}}$		用洞渊九容公式计算

第四卷

底勾17问：已知${\displaystyle a_{3}}$及另一边求直径d.[8]

。

第三卷边股问与第四卷同次第底勾问成对偶。

问	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
第二边	${\displaystyle c_{5}}$	${\displaystyle b_{10}}$	${\displaystyle a_{10}}$	${\displaystyle b_{14}}$	${\displaystyle b_{15}}$	${\displaystyle c_{11}}$	${\displaystyle c_{13}}$	${\displaystyle c_{1}}$	${\displaystyle c_{9}}$	${\displaystyle a_{15}}$	${\displaystyle b_{11}}$	${\displaystyle c_{14}}$	${\displaystyle c_{15}}$	${\displaystyle c_{9}}$	${\displaystyle c_{7}}$	${\displaystyle a_{15}+c_{15}}$	${\displaystyle b_{14}+c_{14}}$

第五卷

大股18问：已知${\displaystyle b_{1}}$。[8]

问	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
第二边	${\displaystyle b_{14}}$	${\displaystyle a_{14}}$	${\displaystyle a_{15}}$	${\displaystyle b_{15}}$	${\displaystyle b_{11}}$	${\displaystyle a_{11}}$	${\displaystyle c_{10}}$	${\displaystyle c_{4}}$	${\displaystyle c_{2}}$	${\displaystyle c_{1}}$	${\displaystyle c_{6}}$	${\displaystyle c_{9}-a_{11}}$	${\displaystyle c_{15}}$	${\displaystyle c_{14}}$	${\displaystyle c_{9}}$	${\displaystyle c_{12}}$	${\displaystyle a_{15}+b_{14}}$	${\displaystyle c_{13}}$

第六卷

大勾18问：

1-11，13-19已知a_{1}，及另一边求直径d.[8]

12问：已知 ${\displaystyle a_{1}+c_{3}}$及另边，求直径。

问	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
已知	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}+c_{3}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$	${\displaystyle a_{1}}$
第二边	${\displaystyle a_{15}}$	${\displaystyle b_{15}}$	${\displaystyle b_{14}}$	${\displaystyle a_{14}}$	${\displaystyle a_{10}}$	${\displaystyle b_{10}}$	${\displaystyle c_{11}}$	${\displaystyle c_{5}}$	${\displaystyle c_{3}}$	${\displaystyle c_{1}}$	${\displaystyle c_{9}}$	${\displaystyle b_{10}-c_{6}}$	${\displaystyle c_{14}}$	${\displaystyle c_{15}}$	${\displaystyle c_{6}}$	${\displaystyle c_{12}}$	${\displaystyle a_{15}+b_{14}}$	${\displaystyle a_{13}}$

第七卷

明叀前18问；求直径d。[9]

问	已知
1	${\displaystyle a_{14}}$，${\displaystyle b_{15}}$
2	${\displaystyle a_{15}}$，${\displaystyle b_{14}}$
3	${\displaystyle a_{14}}$，${\displaystyle a_{15}}$
4	${\displaystyle b_{14}}$，${\displaystyle b_{15}}$
5	${\displaystyle a_{14}}$，${\displaystyle c_{8}}$
6	${\displaystyle b_{15}}$，${\displaystyle c_{7}}$
7	${\displaystyle b_{15}}$，${\displaystyle c_{13}}$
8	${\displaystyle a_{14}}$，${\displaystyle c_{13}}$
9	${\displaystyle d-a_{14}}$，${\displaystyle d-b_{15}}$
10	${\displaystyle d-b_{14}}$，${\displaystyle d-a_{15}}$
11	${\displaystyle c_{12}}$，${\displaystyle a_{15}+b_{14}}$
12	${\displaystyle a_{15}+b_{14}}$，${\displaystyle c_{13}}$
13	${\displaystyle b_{15}+c_{13}}$，${\displaystyle c_{13}-b_{15}}$
14	${\displaystyle a_{14}+b_{15}+c_{13}}$，${\displaystyle a_{14}+b_{15}+c_{13}-a_{14}}$，
15	${\displaystyle c_{14}}$，${\displaystyle d-b_{15}}$
16	${\displaystyle c_{5}}$，${\displaystyle d-a_{14}}$
17	${\displaystyle a_{1}-a_{14}}$，${\displaystyle b_{1}-b_{15}}$
18	${\displaystyle a_{1}+a_{14}}$，${\displaystyle b_{1}-b_{15}}$

第八卷

边股17问：已知 三至八边，或其差，和，求直径d.[10]

问	已知
1	${\displaystyle a_{14}+b_{14}}$，${\displaystyle a_{15}+b_{15}}$，${\displaystyle c_{12}}$
2	${\displaystyle a_{14}+b_{14}}$，${\displaystyle a_{15}+b_{15}}$，${\displaystyle c_{13}}$
3	${\displaystyle (c_{12}-a_{12})+(c_{12}-b_{12})}$，${\displaystyle d_{14}+d_{15}}$
4	${\displaystyle c_{15}}$，${\displaystyle c_{14}}$
5	${\displaystyle b_{14}+c_{14}}$，${\displaystyle c_{15}+b_{15}}$
6	${\displaystyle a_{15}+c_{15}}$，${\displaystyle a_{14}+c_{14}}$
7	${\displaystyle a_{1}+c_{1}}$，${\displaystyle a_{15}+c_{15}}$${\displaystyle }$
8	${\displaystyle a_{1}+c_{1}}$，${\displaystyle a_{14}+c_{14}}$${\displaystyle }$
9	${\displaystyle b_{1}+c_{1}}$，${\displaystyle b_{15}+c_{15}}$${\displaystyle }$
10	${\displaystyle b_{1}+c_{1}}$，${\displaystyle b_{14}+c_{14}}$，${\displaystyle }$
11	${\displaystyle b_{14}+c_{14}}$，${\displaystyle a_{15}+c_{15}}$，${\displaystyle b_{14}+a_{15}-c_{13}}$
12	${\displaystyle (b_{8}-a_{8})+(b_{2}-a_{2})}$，${\displaystyle b_{14}+a_{15}-c_{13}}$${\displaystyle }$
13	${\displaystyle b_{7}-a_{8}}$，${\displaystyle (b_{14}-a_{14})+(b_{15}-a_{15})}$，${\displaystyle c_{12}-d}$
14	${\displaystyle (b_{7}-a_{7})+(b_{8}-a_{8})}$，${\displaystyle (b_{14}-a_{14})+(b_{15}-a_{15})}$${\displaystyle }$
15	${\displaystyle a_{14}+b_{14}}$，${\displaystyle a_{15}+b_{15}}$${\displaystyle }$
16	${\displaystyle a_{14}+a_{15}}$，${\displaystyle b_{14}+b_{15}}$${\displaystyle }$

第十四问

或问：高差，平差并一百六十一步，明差叀差并七十七步，问答同前。

即：

草曰：[11]

已知

${\displaystyle (b_{7}-a_{7})+(b_{8}-a_{8})=161}$

${\displaystyle (b_{14}-a_{14})+(b_{15}-a_{15})=77}$

相加除2 ; 根据#杂用公式，等于皇极差：

${\displaystyle (b_{7}-a_{7})+(b_{8}-a_{8})+(b_{14}-a_{14})+(b_{15}-a_{15}) \over 2}$ ${\displaystyle =(b_{12}-a_{12})}$

${\displaystyle b_{12}-a_{12}=}$${\displaystyle 161+77 \over 2}$${\displaystyle =119}$

设天元一为上平勾：

${\displaystyle x=a_{8}}$

${\displaystyle x+161}$ =${\displaystyle x+(b_{7}-a_{7})+(b_{8}-a_{8})=a_{8}+(b_{7}-a_{7})+(b_{8}-a_{8})}$

${\displaystyle =b_{7}}$ (杂用公式)

因为 ${\displaystyle a_{8}+b_{7}=c_{12}}$ (杂用公式)

${\displaystyle c_{12}=x+b_{7}=2*x+(b_{7}-a_{7})+(b_{8}-a_{8})=2*x+161}$

${\displaystyle c_{12}^{2}=(x+b_{7})^{2}=(2*x+161)^{2}=4*x^{2}+644*x+25921}$

${\displaystyle c_{12}^{2}-(b_{12}-a_{12})^{2}}$

${\displaystyle =4*x^{2}+644*x+25921-}$${\displaystyle ((b_{7}-a_{7})+(b_{8}-a_{8})+(b_{14}-a_{14})+(b_{15}-a_{15}))^{2} \over 4}$

${\displaystyle =4*x^{2}+644*x+11760=d}$(圆城直径),

${\displaystyle d^{2}=(4*x^{2}+644*x+11760)^{2}=16*x^{4}+5152*x^{3}+508816*x^{2}[phone]*x+138297600}$

将 ${\displaystyle 4*x}$乘下高股

${\displaystyle 4*x*b_{7}=4*x*(x+(b_{7}-a_{7})+(b_{8}-a_{8}))=4*x*(x+161)=4*x^{2}+644*x}$

乘之以皇极弦幂:

${\displaystyle d^{2}=4*x*b_{7}*c_{12}^{2}=}$${\displaystyle (4*x^{2}+644*x)*(4*x^{2}+644*x+25921)=}$${\displaystyle 16*x^{4}+5152*x^{3}+518420*x^{2}[phone]}$

因此

${\displaystyle 16*x^{4}+5152*x^{3}+518420*x^{2}[phone]=}$${\displaystyle 16*x^{4}+5152*x^{3}+508816*x^{2}[phone]*x+138297600}$

左右相消得：

${\displaystyle 9604*x^{2}+1546244*x-138297600=0}$

解之得 ${\displaystyle x=a_{8}=64}$;

正合#今问正数中的下平勾。

第九卷上

：大斜四问[12]

问	已知
1	${\displaystyle a_{12}+b_{12}+c_{12}}$，${\displaystyle b_{12}-a_{12}}$
2	${\displaystyle c_{1}}$，${\displaystyle b_{1}-a_{1}}$
3	${\displaystyle c_{1}}$，${\displaystyle a_{10}+b_{11}}$
4	${\displaystyle c_{1}}$，${\displaystyle a_{2}+b_{3}}$

第九卷下

：大和8问

边股17问：已知三边，求直径d[13]。

问	已知条件
1	${\displaystyle a_{1}+b_{1}}$，${\displaystyle a_{2}}$，${\displaystyle b_{3}}$
2	${\displaystyle a_{1}+b_{1}}$，${\displaystyle c_{13}+b_{13}-a_{13}}$，${\displaystyle c_{13}-b_{13}+a_{13}}$
3	${\displaystyle a_{1}+b_{1}}$，${\displaystyle a_{11}+b_{11}}$，${\displaystyle a_{10}+b_{10}}$
4	${\displaystyle a_{1}+b_{1}}$，${\displaystyle c_{10}-a_{10}}$，${\displaystyle c_{11}-b_{11}}$
5	${\displaystyle a_{1}+b_{1}}$，${\displaystyle c_{6}+c_{8}}$，${\displaystyle c_{6}-c_{8}}$
6	${\displaystyle a_{1}+b_{1}}$，${\displaystyle c_{10}}$，${\displaystyle c_{11}}$
7	${\displaystyle a_{1}+b_{1}}$，${\displaystyle c_{4}}$，${\displaystyle c_{5}}$
8	${\displaystyle a_{1}+b_{1}}$，${\displaystyle c_{2}}$，${\displaystyle c_{3}}$

第十卷

：三事和8问[14]

问	已知
1	${\displaystyle a_{1}+b_{1}+c_{1}}$，${\displaystyle c_{1}-b_{1}}$
2	${\displaystyle a_{1}+b_{1}+c_{1}}$，${\displaystyle c_{1}-a_{1}}$
3	${\displaystyle a_{1}+b_{1}+c_{1}}$，${\displaystyle b_{1}-a_{1}}$
4	${\displaystyle a_{1}+b_{1}+c_{1}}$，${\displaystyle (c_{1}-b_{1})+(c_{1}-a_{1})}$
5	${\displaystyle a_{1}+b_{1}+c_{1}}$，${\displaystyle (c_{1}-b_{1})+(b_{1}-a_{1})+(c_{1}-a_{1})}$
6	${\displaystyle a_{1}+b_{1}+c_{1}}$，${\displaystyle d_{14}+d_{15}}$
7	${\displaystyle a_{1}+b_{1}+c_{1}}$，${\displaystyle c_{12}}$
8	${\displaystyle a_{1}+b_{1}+c_{1}}$，${\displaystyle c_{13}}$

第十一卷

杂糅18问：[15]

第十七问，十八问取自《洞淵算书》。

问	已知
1	${\displaystyle c_{2}}$，${\displaystyle c_{3}}$${\displaystyle }$
2	${\displaystyle c_{5}}$，${\displaystyle c_{4}}$${\displaystyle }$
3	${\displaystyle b_{11}}$，${\displaystyle c_{4}}$${\displaystyle }$
4	${\displaystyle a_{10}}$，${\displaystyle c_{3}}$${\displaystyle }$
5	${\displaystyle a_{10}}$，${\displaystyle b_{11}}$${\displaystyle }$
6	${\displaystyle b_{7}}$，${\displaystyle a_{8}}$${\displaystyle }$
7	${\displaystyle b_{1}-b_{11}}$，${\displaystyle a_{1}-a_{10}}$
8	${\displaystyle b_{10}-a_{10}}$，${\displaystyle b_{11}-a{11}}$${\displaystyle }$
9	${\displaystyle c_{13}}$，${\displaystyle a_{10}-b_{11}}$${\displaystyle }$
10	${\displaystyle a_{12}+b_{12}}$，${\displaystyle a_{13}+b_{13}}$${\displaystyle }$
11	${\displaystyle c_{1}}$，${\displaystyle b_{1} \over a_{1}}$${\displaystyle }$
12	${\displaystyle d_{10}-d_{11}}$，${\displaystyle d_{12}-d_{13}}$${\displaystyle }$
13	${\displaystyle c_{12}-[c_{10}-(b_{10}-a_{10})]}$，${\displaystyle c_{11}+(b_{11}-a_{11})-c_{13}}$，${\displaystyle b_{12}-a_{12}}$
14	${\displaystyle c_{8}-(c_{1}-b_{1})}$，${\displaystyle (c_{1}-a_{1})-c_{7}}$${\displaystyle }$
15	${\displaystyle a_{1}+c_{1}}$，${\displaystyle (c_{1}-a_{1})+(c_{1}-b_{1})}$${\displaystyle }$
16	${\displaystyle a_{12}+b_{12}+c_{12}}$，${\displaystyle (a_{13}+b_{13})-c_{13}}$${\displaystyle }$
17	(取自《洞淵算书》）
18	取自《洞淵算书》

第十二卷

之分14问[16]

问	已知
1	${\displaystyle b_{1}+c_{1}}$，${\displaystyle a_{1}}$= ${\displaystyle 8 \over 15}$${\displaystyle b_{1}}$
2	${\displaystyle a_{1}+c_{1}}$，${\displaystyle a_{1}}$= ${\displaystyle 8 \over 15}$${\displaystyle b_{1}}$
3	${\displaystyle a_{1}=(1-5/9)*3d}$，${\displaystyle b_{1}-a_{1}}$${\displaystyle }$
4	${\displaystyle a_{3}=(5/6)*d}$，${\displaystyle b_{2}-a_{3}}$
5	${\displaystyle (15/16)b_{1}=d}$，${\displaystyle a_{1}+b_{1}}$${\displaystyle }$
6	${\displaystyle a_{12}=(8/15)*b_{12}}$，${\displaystyle c_{12}-b_{12}}$，${\displaystyle c_{12}-a_{12}}$
7	${\displaystyle c_{1}}$，${\displaystyle d=(1/2)b_{2}}$，${\displaystyle a_{3}=(5/6)d}$
8	${\displaystyle b_{2}+a_{3}+c_{2}}$，${\displaystyle b_{2}=(12/17)c_{1}}$，${\displaystyle a_{3}=(5/17)c_{1}}$
9	${\displaystyle a_{3}+(5/6)b_{2}}$，${\displaystyle b_{2}+(3/5)a_{3}}$${\displaystyle }$
10	${\displaystyle a_{11}+(1/3)b_{10}}$，${\displaystyle b_{10}-(3/4)a_{11}}$${\displaystyle }$
11	${\displaystyle b_{1}-d=(3/5)b_{1}}$，${\displaystyle a_{1}-d=(1/4)a_{1}}$，${\displaystyle (b_{1}-d)-(a_{1}-d)}$
12	${\displaystyle b_{1}-d=(3/5)b_{1}}$，${\displaystyle a_{1}-d=(1/4)a_{1}}$，${\displaystyle (1/5)b_{1}-(1/4)a_{1}}$
13	${\displaystyle b_{14}=(1-(15/24)b_{10})}$，${\displaystyle a_{15}=(1-(4/5))a_{11}}$，${\displaystyle b_{14}-a_{15}}$,${\displaystyle b_{10}-a_{11}}$
14	${\displaystyle a_{1}+b_{1}+c_{1}}$，${\displaystyle (b_{1}/a_{1})=8(1/3)}$，${\displaystyle (a_{1}/b_{15})=10(2/3)}$，${\displaystyle a_{14}-a_{13}}$，${\displaystyle b_{13}-b_{15}}$

版本

天元术并非李冶的独创，而是从金代起便在中国北方开始萌芽。据祖颐在《四元玉鉴后序》中的记载，李冶以前研究天元术的学者有北宋蒋周撰《益古集》、李文一撰《照胆》，石信道撰《钤经》、刘汝谐撰《如积释锁》等书，世人才知道有天元。此外朱世杰《四元玉鉴》引用北宋《洞渊九容细草》两道题，其中有“立天元一”[17]。后来李德载撰《两仪群英集臻》兼有地元。1306年元刻本《阴阳备用三元节要》三卷下有天元，地元[18]。但是这些早期天元术的著作已经失传。宋代《杨辉算法》保留蒋周《益古集》的一些条段法的题目，没保留天元术的内容。现存元刻本《阴阳备用三元节要》只有一条二元术题，《测圆海镜》是现存最早的系统地讲述天元术的著作。

到了明代，天元术因为艰深难懂而少人研究，几近失传。明代唐顺抄录过《测圆海镜》，但不懂天元术；顾应祥曾经撰写《测圆海镜分类释术》，但完全没有明白天元术中天元为未知数的含义，因而将《测圆海镜》中关于立天元列方程的演算全部删去，只留下用开方术解方程的过程，以便后人学习[19]。李俨认为宋金元发展起来的天元术至此已被遗忘[20]。《测圆海镜分类释术》一书，虽然删除了天元术内容，但保存了全部算题，也补入正确的几何学解法，使得几近失传的《测圆海镜》，得以从新流传[21]。

十八世纪时，随着西洋算学传入中国，李冶等人的天元术著作才被后来的数学家重新发现。戴东原从《永乐大典》中辑录出李冶《测圆海镜》[22]；清朝梅瑴成（梅文鼎之孙）曾经研读元学士李冶的《测圆海镜》，对其中的天元之术感到不解，后来在研习西方的“借根方”法时发现所谓的“借根”就是“立天元”（都是设未知数），方才重新开始认识天元术[23][24]。之后，《四元玉鉴》等其它天元术著作也被重新认识。孔广森曾校对《测圆海镜》中的四章。乾隆三十八年（1773年），《四库全书》收录了李潢家藏本的《测圆海镜》。1798年，清代大藏书家鲍廷博刊印的《知不足斋丛书》中收录了李锐校勘的《测圆海镜细草》十二卷[25]。之后又有焦循和李锐在研究了《测圆海镜》、《益古演段》和《数书九章》后写的《天元一释》和《开方通释》两书，用较为明白的语言详细解释了李冶的天元术和秦九韶的正负开方术。1873年，张楚钟发表《测圆海镜通释》对《识别杂记》中的几百条定理，用几何方法逐条证明。

清代研究

1896年刘岳云出版《测圆海镜解》，发现《圆城图式》中各线段的简单加减关系，发表《诸率加减表》，此后李善兰出版《测圆海镜解》等[26]。他在另一篇著作《天算或问》中给出勾股容圆各公式的统一公式。其后陈维祺发表《各率及较泛积表》将《识别杂记》用“泛积”概念统一表示[27]。王季同在《九容公式》中进一步发展了陈维祺的成果，发现[28]

极勾=(高股 * 平勾 +平勾^2)^(1/2)

极股=(高股 * 平勾 +高股^2)^(1/2)

半径=(高股 * 平勾 )^(1/2)

国际研究

19世纪初，朝鲜数学家南秉哲著《海镜细草解》。

1913年，法国学者L.van Hoe 介绍《测圆海镜》。1982年，法国林力娜（K. Chemla)作论文 Etude du Livre Reflects des Mesuers du Cercle sur la mer de Li Ye，获得博士学位。1983年，新加坡大学教授蓝丽蓉发表 Chinese Polynomial Equations in the Thirteenth Century,论述《测圆海镜》。

评价

清代数学家对《测圆海镜》给予很高评价。阮元认为《测圆海镜》是“中土数学之宝书”，李善兰称赞它是“中华算书，无有胜于此者”。白尚恕说，《测圆海镜》的成就，超过同时期的印度，阿拉伯和欧洲，“处于世界数学里遥遥领先的地位”[29]

参考文献

引用

1. 中国古代数学，《测海圆镜》. [2009-10-31]. （原始内容存档于2020-10-23）. 
2. 孔国平著. 《测圆海镜今导读》 《今问正数》 62-66 页 湖北教育出版社. 1995
3. 李冶 著 白尚恕 译 钟善基 校. 《测圆海镜今译》 24-25页 山东教育出版社. 1985.
4. 吴文俊主编 《中国数学史料大系》 第六卷 第二章 80页
5. 李冶《自序》“老大以來，得洞淵九容之說，日夕玩繹，而向之病我者，使爆然落去而無遺餘”
6. 《李俨.钱宝琮科学史全集》卷8，李俨《测圆海镜研究历程考》 45-48 页辽宁教育出版社. 1998
7. 《李俨.钱宝琮科学史全集》卷8，李俨《测圆海镜研究历程考》75-88页
8. 《李俨.钱宝琮科学史全集》卷8，李俨《测圆海镜研究历程考》88-101页
9. 孔国平著. 《测圆海镜今导读》169-184 湖北教育出版社. 1995
10. 孔国平著. 《测圆海镜今导读》 192-208 湖北教育出版社. 1995
11. 白尚恕, 562-566页
12. 孔国平著. 《测圆海镜今导读》. 205-208页 湖北教育出版社. 1995
13. 《李俨.钱宝琮科学史全集》卷8，李俨《测圆海镜研究历程考》181-195页
14. 孔国平著. 《测圆海镜今导读》220-224页 湖北教育出版社. 1995
15. 孔国平 著. 《测圆海镜今导读》234-248页 湖北教育出版社. 1995
16. 孔国平 著. 《测圆海镜今导读》255-263 湖北教育出版社. 1995
17. 孔国平著 《测圆海镜导读·引论》 6页 ISBN 7-5351-1972-7
18. 《李俨.钱宝琮科学史全集》卷10，李俨《中国数学的历史发展》 474页 辽宁教育出版社. 1998
19. 顾应祥，《测圆海镜分类释术》序：“每章去其細草，立一算術，……各以類分之，語義稍繁者，略加芟損，名曰《測圓海鏡分類釋術》。非敢僭改前賢著述，惟以便下學云爾”
20. 李俨，《中国算学史》，第七章第四 近世期（四）顾应祥
21. 孔国平，《测圆海镜导读序》
22. 梁启超《饮冰室合集》 第十卷 343页 《中国近三百年学术史》 中华书局
23. 柯劭忞等，《清史稿·列传二百九十三》畴人一：“明代算家，不解立天元术，瑴成谓立天元一即西法之借根方，其说曰；“尝读授时历草求弦矢之法，先立天元一为矢，而元学士李冶所著测圜海镜，亦用天元一立算。传写鲁鱼，算式讹舛，殊不易读。明唐荆川、顾箬溪两公互相推重，自谓得此中三昧。荆川之说曰：‘艺士著书，往往以秘其机为奇，所谓天元一云尔，如积求之云尔，漫不省其为何语。’而箬溪则言：‘细考测圜海镜，如求城径，即以二百四十为天元，半径即以一百二十为天元，即知其数，何用算为？似不必立可也。’二公之言如此，余于顾说颇不谓然，而无以解也。后供奉内廷，蒙圣祖仁皇帝授以借根之法，且谕曰：‘西人名此书为阿尔热八达，译言东来法也。’敬受而读之，其法神妙，诚算法之指南，而窃疑天元一之术颇与相似。复取授时历草观之，乃焕然冰释，殆名异而实同，非徒似之而已。”
24. 阮元，《畴人传》卷二十四，李冶传
25. 李冶，《测圆海镜细草》，知不足斋刻本
26. 李善蘭，《測圓海鏡解》，抄本，存中國科學院自然科學史研究所
27. 孔国平著. 《测圆海镜今导读》24-30 湖北教育出版社. 1995
28. 孔国平著. 《测圆海镜今导读》 30页 湖北教育出版社. 1995
29. 李冶 著 白尚恕 译 钟善基 校. 《测圆海镜今译》 1页 山东教育出版社. 1985

来源

书籍

• 李人言. 《中國算學史》. 台灣商務印書館. 1965年. 
• 孔国平. 《李冶朱世杰与金元数学》. 河北科学技术出版社. 2000年. ISBN 978-7-537-51884-0. 

参见

• 李冶《益古演段》
• 朱世杰《四元玉鉴》
• 李善兰
• 秦九韶算法