側錐球狀屋頂

側錐球狀屋頂

類別	詹森多面體 J86 - J87 - J88
識別
名稱	側錐球狀屋頂 augmented sphenocorona
別名	側錐球形屋根（日語）
參考索引	J87
鮑爾斯縮寫 （verse-and-dimensions的wikia：Bowers acronym）	auwaco
性質
面	17
邊	26
頂點	11
歐拉特徵數	F=17, E=26, V=11 （χ=2）
組成與佈局
面的種類	4+6×2個三角形 1個正方形
頂點圖	1個(3^4) 2個(3^3.4) 3×2個(3^5) 2個(3^4.4)
對稱性
對稱群	Cs群
特性
凸
圖像
（展開圖）
查 论 编

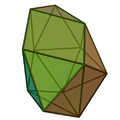
側錐球狀屋頂（日語：側錐球形屋根、英語：Augmented sphenocorona）是一種由16個三角形和1個正方形組成的十七面體[1]，為詹森多面體的其中一個，索引為J₈₇[2]。它雖然可由球狀屋頂（J₈₆）於正方形面上增加一正四角錐（J₁）來構成[2]，但無法由柏拉圖立體（正多面體）和阿基米得立體（半正多面體）經過切割、增補而得來。詹森多面體是凸多面體，面皆由正多邊形組成但不屬於均勻多面體，共有92種。這些立體最早在1966年由諾曼·詹森（英语：Norman Johnson (mathematician)）（Norman Johnson）命名並給予描述[3]。

性質

側錐球狀屋頂共由17個面、26條邊和11個頂點所組成[4][5][6][7]。在其17個面中，有16個三角形面和1個正方形面[5]。在其11個頂點中有1個頂點是4個三角形的公共頂點[7]，在頂點圖中可以用[3^4]來表示[8]、還有6個頂點是5個三角形的公共頂點[7]，在頂點圖中可以用[3^5]來表示[8]、還有2個頂點是3個三角形和1個正方形的公共頂點，在頂點圖中可以用[3^3,4]來表示[8]、剩下的2個頂點是4個三角形和1個正方形的公共頂點，在頂點圖中可以用[3^4,4]來表示[8]。

構成

側錐球狀屋頂可以透過在球狀屋頂（J₈₆）的正方形面上疊上一個正四角錐構成，疊上之後正四角錐側面與球狀屋頂另一個正方形面的角度將會非常接近平角，幾乎是共面的，但還未達到共面的狀態：其二面角約為171.8°。[6]

體積與表面積

若一個側錐球狀屋頂邊長為${\displaystyle a}$，則其表面積${\displaystyle A}$為：[9]

${\displaystyle A=\left(1+4{\sqrt {3}}\right)a^{2}\approx 7.92820a^{2},}$[10]

而其體積${\displaystyle V}$為：

${\displaystyle V=\left({\frac {1}{2}}{\sqrt {1+3{\sqrt {\frac {3}{2}}}+{\sqrt {13+3{\sqrt {6}}}}}}+{\frac {1}{3{\sqrt {2}}}}\right)a^{3}\approx 1.75105a^{3}.}$[11]

頂點座標

要計算側錐球狀屋頂的頂點座標可以從球狀屋頂開始計算，然後再補上側錐多出來的頂點。邊長為2的球狀屋頂的頂點座標之計算可以先令k ≈ 0.85273為下列四次式的最小實根：

${\displaystyle 60x^{4}-48x^{3}-100x^{2}+56x+23.}$

則邊長為2的球狀屋頂之頂點座標可以由下列頂點的軌道的並集在沿xz平面和yz平面鏡射所產生的空間對稱群之群作用下給出：[12]

${\displaystyle \left(0,1,2{\sqrt {1-k^{2}}}\right),\,(2k,1,0),\left(0,1+{\frac {\sqrt {3-4k^{2}}}{\sqrt {1-k^{2}}}},{\frac {1-2k^{2}}{\sqrt {1-k^{2}}}}\right),\,\left(1,0,-{\sqrt {2+4k-4k^{2}}}\right)}$

最後計算其中一個正方形面的質心和該正方形面的法向量後，可以得出其最後一個頂點的位置為：

${\displaystyle \left(k+{\sqrt {2-2k^{2}}},0,k+{\sqrt {2-2k^{2}}}\right).}$

另一個角度的邊長為2的側錐球狀屋頂頂點座標也可以表示為：[6]

${\displaystyle \left(0,\,0,\,\pm 1\right)}$

${\displaystyle \left(\pm A,\,{\sqrt {B}},\,\pm 1\right)}$

${\displaystyle \left(0,\,{\sqrt {C}},\,\pm D\right)}$

${\displaystyle \left(\pm 1,\,{\sqrt {E}},\,0\right)}$

${\displaystyle \left({\frac {A+B{\sqrt {2}}}{2}},\,{\frac {B-A{\sqrt {2}}}{2}},\,0\right)}$

其中，${\displaystyle A}$、${\displaystyle B}$、${\displaystyle C}$、${\displaystyle D}$和${\displaystyle E}$為下列方程式的實根：[6]

${\displaystyle 15A^{4}-24A^{3}-100A^{2}+112A+92=0,\qquad 1\leqslant A\leqslant 2}$

${\displaystyle 225B^{4}-24B^{3}-3176B^{2}-96B+3600=0,\qquad 1\leqslant B\leqslant 2}$

${\displaystyle 225C^{4}-24C^{3}-3176C^{2}-96C+3600=0,\qquad 3\leqslant C\leqslant 4}$

${\displaystyle 15D^{4}-36D^{3}-82D^{2}+100D+95=0,\qquad 1\leqslant D\leqslant 2}$

${\displaystyle E^{2}-4E-20=0,\qquad 6\leqslant E\leqslant 7}$

其中，${\displaystyle B}$和${\displaystyle C}$是同個方程式但不同實根。${\displaystyle E}$可以表達為${\displaystyle 2+2{\sqrt {6}}}$。[6]

這些數值的近似值為：[6]

${\displaystyle A}$ ≈ 1.705453885692834

${\displaystyle {\sqrt {B}}}$ ≈ 1.044713857367277

${\displaystyle {\sqrt {C}}}$ ≈ 1.914399800381786

${\displaystyle D}$ ≈ 1.578855253321743

${\displaystyle {\sqrt {E}}}$ ≈ 2.626590848527109

相關多面體

• 
  球狀屋頂
  （原始的球狀屋頂立體）
• 
  球狀屋頂欠側錐
  （移除一個五角錐的球狀屋頂）
• 
  側錐球狀屋頂
  （在正方形面疊上正四角錐的球狀屋頂）
• 
  加長型球狀屋頂
  （正方形附近的4個位置上各加上1個正三角形的球狀屋頂）
• 
  廣底加長型球狀屋頂
  （「屋頂」部分由3個正方形組成的球狀屋頂）
• 
  廣底加長型球狀屋頂欠側錐
  （移除一個五角錐的廣底加長型球狀屋頂）
• 
  五角錐球狀屋頂
  （合併兩個移除了兩個正三角形的球狀屋頂）

參見

• 詹森多面體
• 球狀屋頂
• 正四角錐
• 多面體

參考文獻

1. Santiago Alvarez. Polyhedra in (Inorganic) Chemistry (PDF). Electronic Supplementary Information for Dalton Transactions. 2005 [2022-09-25]. （原始内容存档 (PDF)于2022-01-21）. 
2. Weisstein, Eric W. (编). Augmented Sphenocorona. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
3. Johnson, Norman W.（英语：Norman Johnson (mathematician)）, Convex polyhedra with regular faces, Canadian Journal of Mathematics（英语：Canadian Journal of Mathematics）, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8 .
4. V.Bulatov. augmented sphenocorona. [2022-09-11]. （原始内容存档于2022-12-07）. 
5. David I. McCooey. Johnson Solids: Augmented Sphenocorona. [2022-09-07]. （原始内容存档于2022-09-11）. 
6. The Augmented Sphenocorona. qfbox.info. [2022-09-11]. （原始内容存档于2022-12-31）. 
7. Augmented sphenocorona. polyhedra.tessera.li. [2022-09-11]. （原始内容存档于2023-01-03）. 
8. Richard Klitzing. augmented sphenocorona, auwaco. bendwavy.org. [2022-09-11]. （原始内容存档于2022-11-14）. 
9. Wolfram, Stephen. "Augmented Sphenocorona". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）. 
10. Wolfram Research, Inc. Wolfram|Alpha Knowledgebase. Champaign, IL. 2020. PolyhedronData[{"Johnson", 87}, "SurfaceArea"] 
11. Wolfram Research, Inc. Wolfram|Alpha Knowledgebase. Champaign, IL. 2020. PolyhedronData[{"Johnson", 86}, "Volume"] + PolyhedronData["SquarePyramid", "Volume"] 
12. Timofeenko, A. V. The non-Platonic and non-Archimedean noncomposite polyhedra. Journal of Mathematical Science. 2009, 162 (5): 718. S2CID 120114341. doi:10.1007/s10958-009-9655-0. 

外部連結

• 埃里克·韦斯坦因. Johnson Solid. MathWorld. 
  • 埃里克·韦斯坦因. Augmented sphenocorona. MathWorld.