十七面體

十七面體

部分的十七面體
	三側錐六角柱
正五角罩帳	側錐球狀屋頂

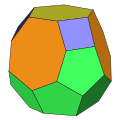
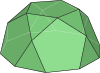
在幾何學中，十七面體是指有17個面的多面體，在十七面體當中沒有任何一個形狀是正多面體，換言之即正十七面體並不存在，但仍然有接近球形的十七面體，例如一些十七面體型的化學結構[1][2]，但時其面並非由正多邊形組成，雖然仍有許多由正多邊形組成的十七面體，例如正五角罩帳和側錐球狀屋頂[3]，但其對稱性較低。此外，也存在非常多拓樸結構有明顯差異的十七面體，例如十六角錐和十五角柱。

工業上十七面體有許多用途，例如特殊設計的十七面體可以減少空隙方便堆放[4][5]。

凸十七面體

在所有凸十七面體當中，拓樸結構有明顯差異的凸十七面體，包含其鏡射像共有6,415,851,530,241種凸十七面體有著至少11個頂點[6]。兩者具有不同的拓撲結構是代表他們面和頂點有不同的安排方式，使得其無法單靠扭曲或簡單地通過改變邊或面之間的長度或角度轉換成另一種多面體的多面體。

此外由於無窮拉夫斯圖的對稱性是從三維空間的二十面體堆砌而來，因此具有凸十七面體的沃羅諾伊胞[7]。

一些凸十七面體的例子比如八角錐柱[8]、正五角罩帳、凸三側錐六角柱、側錐球狀屋頂。

非凸十七面體

在幾何學上也有許多非凸十七面體，像是星形柱體、錐體或台體，如五角錐五角星台[9]。

常見的十七面體

十五角柱

十五角柱

十五角柱是一種底面為十五邊形的柱體，是十七面體的一種，由17個面45條邊和30個頂點組成。正十五角柱代表每個面都是正多邊形的十五角柱，其每個頂點都是2個正方形和1個十五邊形的公共頂點，頂點圖以${\displaystyle 4{.}4{.}15}$表示，因此具有每個角等角的性質（點可遞），可以歸類為半正十七面體，不過他跟其他較接近球形的半正多面體相比之下變得比較扁一些。

正十五角柱在施萊夫利符號中可以用{15}×{}或t{2,15}來表示，在考克斯特符號（英语：Coxeter-Dynkin diagram）中可以用來表示，在威佐夫符號（英语：Wythoff symbol）中可以利用2 15 | 2來表示，在康威多面體表示法中可以利用P15來表示。底邊長為${\displaystyle s}$、高為${\displaystyle h}$的正十五角柱體積${\displaystyle V}$和表面積${\displaystyle S}$為[10]：

${\displaystyle V={\frac {15hs^{2}\cot {\frac {\pi }{15}}}{4}}\approx 17.6424hs^{2}}$

${\displaystyle S=15s\left(h+{\frac {s\cot {\frac {\pi }{15}}}{2}}\right)\approx 15s\left(h+2.35232s\right)}$

十六角錐

十六角錐

十六角錐是一種底面為十六邊形的錐體，是十七面體的一種，具有17個面、32條邊和17個頂點，其對偶多面體是自己本身。[11]正十六角錐是指底面為正十六邊形的十六角錐，在施萊夫利符號中可以用{}∨{16}來表示。底邊長為${\displaystyle s}$、高為${\displaystyle h}$的正十六角錐體積${\displaystyle V}$和表面積${\displaystyle S}$為[11]：

${\displaystyle V={\frac {4hs^{2}\cot {\frac {\pi }{16}}}{3}}\approx 6.70312hs^{2}}$

${\displaystyle S=4s\left({\sqrt {4h^{2}+s^{2}\cot ^{2}{\frac {\pi }{16}}}}+s\cot {\frac {\pi }{16}}\right)\approx 4s\left({\sqrt {4h^{2}+25.2741s^{2}}}+5.02734s\right)}$

八角錐柱

八角錐柱是指底面為八邊形的角錐柱，由17個面、32條邊和17個頂點組成，是一種十七面體。

五角罩帳

正五角罩帳

五角罩帳是以五邊形為底的罩帳，是一種十七面體，由1個五邊形頂面、1個十邊形底面、6個五邊形側面和10個三角形側面組成，共有15個面、35條邊和20個頂點，其中五邊形頂面與十邊形底面互相平行，三角形側面與五邊形側面交錯地圍繞軸分佈在周圍。

以正五邊形為底的五角罩帳稱為正五角罩帳。正五角罩帳可以頂面和側面的五邊形都為正五邊形，此時的正五角罩帳所有面都是正多邊形，是一種詹森多面體，也是唯一一個屬於詹森多面體的罩帳[12]。

正五角罩帳的對稱群為C_5v（英语：Dihedral symmetry in three dimensions）群，階數為10階。

三角帳塔罩帳

三角帳塔罩帳是指底面為三角形的帳塔罩帳，由三角帳塔和三角罩帳以邊數較多的底面互相貼合疊合而成，是一種十七面體。三角帳塔罩帳共有17個面、30條邊和15個頂點所組成。在其17個面中，有2個三角形底面、9個三角形側面、3個矩形側面和3個五邊形側面。

三角帳塔罩帳依照三角帳塔和三角罩帳的貼合方式可以分成同相三角帳塔罩帳和異相三角帳塔罩帳。

同相三角帳塔罩帳

異相三角帳塔罩帳

十七面體列表

名稱	種類	圖像	符號	頂點	邊	面	χ	面的種類	對稱性	展開圖
十五角柱	稜柱體		t{2,15} {15}x{}	30	45	17	2	2個十五邊形 15個矩形	D15h, [15,2], (*15 2 2), order 60
十六角錐	稜錐體		( )∨{16}	17	32	17	2	1個十六邊形 16個三角形	C16v, [16], (*16 16)
八角錐柱	角錐柱		P8+Y8	17	32	17	2	8個三角形 8個正方形 1個八邊形	C8v, [8], (*88)
八角錐台錐	截角雙錐			17	32	17	2	1個八邊形 8個梯形 8個三角形	C8v, [8], (*88)
十五角錐台	錐台			30	45	17	2	2個十五邊形 15個梯形	D15h, [15,2], (*15 2 2), order 60
五角罩帳	罩帳			20	35	17	2	1個五邊形頂面 1個十邊形底面 5個五邊形側面 10個三角形側面	C5v（英语：Dihedral symmetry in three dimensions）, [5], (*55), order 10
同相三角帳塔罩帳	帳塔罩帳			15	30	17	2	2個三角形底面 9個三角形側面 3個矩形側面 3個五邊形側面	C3v（英语：Dihedral symmetry in three dimensions）
異相三角帳塔罩帳

參考文獻

1. V. Gold. Advances in Physical Organic Chemistry APL 第 14 卷. Academic Press. 1977: 227. ISBN 9780080581538. 
2. Commonwealth Scientific and Industrial Research Organization (Australia), Institute of Physics (Great Britain). Australian Branch, Australian National Research Council, Australian Academy of Science. Australian Journal of Chemistry, 第 52 卷. Commonwealth Scientific and Industrial Research Organization. 1999: 343-822, 497. 
3. Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8 
4. Pedrita, alongside Água de Luso. The bottle’s 17 faces. [2016-08-20]. （原始内容存档于2016-08-20）. 
5. 以節省空間與堆疊的17面體瓶身設計. poloves. [2016-08-20]. （原始内容存档于2014-08-04）. 
6. Counting polyhedra （页面存档备份，存于互联网档案馆） numericana.com [2016-1-10]
7. Schoen, Alan H., On the graph (10,3)-a (PDF), Notices of the American Mathematical Society, June–July 2008, 55 (6): 663 [2016-08-05], （原始内容存档 (PDF)于2016-09-28） .
8. Heptakaidecahedra (polyhedra with 17 faces). korthalsaltes.com. [2016-08-05]. （原始内容存档于2016-10-13）. 
9. Paper Pentagonal-pentagrammic Shape. korthalsaltes.com. [2016-08-05]. （原始内容存档于2016-10-13）. 
10. Wolfram, Stephen. "pentadecagonal prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）. 
11. Wolfram, Stephen. "hexadecagonal pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）. 
12. Johnson, Norman W.（英语：Norman Johnson (mathematician)）, Convex polyhedra with regular faces, Canadian Journal of Mathematics（英语：Canadian Journal of Mathematics）, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8 .