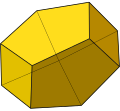
二側錐三角柱 (英文 :Biaugmented triangular prism)屬於詹森多面體 之一(J 50 [ 1] 正四角錐 (J 1 )以底面黏合在一個正三角柱 的兩個側面上組合而成,這與側錐三角柱 (J 49 )和三側錐三角柱 (J 51 )有著極為相似的構造。這92種詹森多面體最早在1966年由詹森·諾曼 [ 2] 2 H6 ZrF6 。[ 3]
二側錐三角柱共由11個面 、17條邊 和8個頂點 組成。[ 4] 三角形 面和1個正方形 面。二側錐三角柱可以視為三角柱 與2個正四角錐 的組合[ 5] :86 ,因此在二側錐三角柱的10個三角形 面又可以分成兩組,一組為側錐的側面,每個側錐有4個正三角形 ,共8個正三角形;以及三角柱 的兩個三角形底面 。[ 6]
若二側錐三角柱邊長為單位長,則其體積
V
{\displaystyle V}
表面積
A
{\displaystyle A}
[ 6]
V
=
4
2
+
3
3
12
≈
0.904417
{\displaystyle V={\frac {4{\sqrt {2}}+3{\sqrt {3}}}{12}}\approx 0.904417}
[ 6]
A
=
1
+
5
3
2
≈
5.33013
{\displaystyle A=1+{\frac {5{\sqrt {3}}}{2}}\approx 5.33013}
[ 7]
若二側錐三角柱邊長為單位長,則其頂點座標為:[ 8]
(
±
1
2
,
±
1
2
,
3
6
)
{\displaystyle \left(\pm {\frac {1}{2}},\,\pm {\frac {1}{2}},\,{\frac {\sqrt {3}}{6}}\right)}
(
0
,
±
1
2
,
−
3
3
)
{\displaystyle \left(0,\,\pm {\frac {1}{2}},\,-{\frac {\sqrt {3}}{3}}\right)}
(
±
1
+
6
4
,
0
,
−
3
2
+
3
12
)
{\displaystyle \left(\pm {\frac {1+{\sqrt {6}}}{4}},\,0,\,-{\frac {3{\sqrt {2}}+{\sqrt {3}}}{12}}\right)}
二側錐三角柱有5種二面角 ,其中分別是2種三角形-正方形交角和3種三角形-三角形交角。[ 9]
其中一種三角形-正方形交角來自於三角柱底面和側面的交稜,二面角為90度 [ 9] 度 :
cos
−
1
(
−
3
2
−
3
6
)
≈
114.73561
∘
{\displaystyle \cos ^{-1}{\left(-{\frac {3{\sqrt {2}}-{\sqrt {3}}}{6}}\right)}\approx 114.73561^{\circ }}
[ 6] 另外三個二面角分別為兩側錐側面的交稜約169.47122度、側錐側面與三角柱底面的交稜約144.73561度、以及同個側錐中兩側面的交稜約109.47122度。[ 9]
兩側錐側面稜的交角
=
cos
−
1
(
−
1
+
2
6
6
)
≈
169.47122
∘
{\displaystyle =\cos ^{-1}{\left(-{\frac {1+2{\sqrt {6}}}{6}}\right)}\approx 169.47122^{\circ }}
[ 6]
側錐側面與三角柱底面稜的交角
=
cos
−
1
(
−
6
3
)
≈
144.73561
∘
{\displaystyle =\cos ^{-1}{\left(-{\frac {\sqrt {6}}{3}}\right)}\approx 144.73561^{\circ }}
[ 6]
同個側錐中兩側面稜的交角
=
cos
−
1
(
−
1
3
)
≈
109.47122
∘
{\displaystyle =\cos ^{-1}{\left(-{\frac {1}{3}}\right)}\approx 109.47122^{\circ }}
[ 6]
根據對偶多面體 的定義,多面體的對偶多面體其面將會是原始多面體的頂點圖 ,[ 10] [ 11] 雙三角錐 。
二側錐三角柱是2個側面被四角錐取代的三角柱 。其他也是側面被取代的三角柱結構有側錐三角柱 和三側錐三角柱 。[ 5] :86
二側錐三角柱是底面為三角形之柱體對應的二側錐柱體,其他的二側錐柱體有:
^ Weisstein, Eric W. (编). Biaugmented Triangular Prism . at MathWorld Wolfram Research, Inc. (英语) . ^ Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18 : 169–200, MR 0185507 Zbl 0132.14603 doi:10.4153/cjm-1966-021-8 ^ Deza, Antoine and Deza, Michel and Grishukhin, Viatcheslav. Fullerenes and coordination polyhedra versus half-cube embeddings. Discrete mathematics (Elsevier). 1998, 192 (1-3): 41–80. ^ Vladimir Bulatov. biaugmented triangular prism . [2021-09-06 ] . (原始内容存档 于2020-11-05). 页面存档备份 ,存于互联网档案馆 )^ 5.0 5.1 Rajwade, A.R. Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. 2001. ISBN 9789386279064 ^ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 David I. McCooey. Johnson Solids : Biaugmented Triangular Prism . dmccooey.com. [2021-09-05 ] . (原始内容存档 于2021-09-12). 页面存档备份 ,存于互联网档案馆 )^ Wolfram, Stephen . " Biaugmented Triangular Prism" Wolfram Alpha : Computational Knowledge Engine, Wolfram Research (英语) . ^ David I. McCooey. Data of Biaugmented Triangular Prism . dmccooey.com. [2021-09-05 ] . (原始内容存档 于2021-09-12). 页面存档备份 ,存于互联网档案馆 )^ 9.0 9.1 9.2 Richard Klitzing. biaugmented triangular prism, bautip . bendwavy.org. [2021-09-12 ] . (原始内容存档 于2021-09-21). 页面存档备份 ,存于互联网档案馆 )^ Weisstein, Eric W. (编). Dual Polyhedron . at MathWorld Wolfram Research, Inc. (英语) . ^ Biaugmented triangular prism . polyhedra.tessera.li. [2021-09-12 ] . (原始内容存档 于2021-09-12). 页面存档备份 ,存于互联网档案馆 )