Monoidale Kategorie

In der Mathematik bezeichnet eine monoidale Kategorie eine Kategorie ${\displaystyle {\mathcal {C}}}$, die mit einem zweistelligen Funktor ${\displaystyle \otimes \colon {\mathcal {C}}\times {\mathcal {C}}\to {\mathcal {C}}}$ und einem Einheitsobjekt ${\displaystyle I\in \left|{\mathcal {C}}\right|}$ ausgestattet ist.

Die Verknüpfung muss assoziativ in dem Sinne sein, dass es eine natürliche Äquivalenz ${\displaystyle \alpha }$,

${\displaystyle \alpha _{A,B,C}\colon (A\otimes B)\otimes C\to A\otimes (B\otimes C),}$

gibt; ${\displaystyle I}$ muss links- und rechtsneutral in dem Sinne sein, dass es natürliche Äquivalenzen ${\displaystyle \lambda }$ und ${\displaystyle \rho }$ gibt, gegeben durch

${\displaystyle \lambda _{A}\colon I\otimes A\to A}$ und ${\displaystyle \rho _{A}\colon A\otimes I\to A}$.

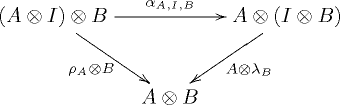
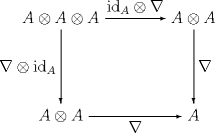
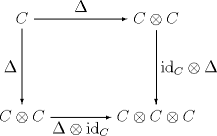
Diese natürlichen Transformationen sollen kohärent sein. Alle nötigen Kohärenzbedingungen folgen aus der Kommutativität der folgenden beiden Diagramme:

und

Aus diesen beiden Bedingungen folgt, dass jedes solche Diagramm kommutiert: Das ist Mac Lanes „Kohärenzsatz“.

• Eine monoidale Kategorie kann als Bikategorie mit einem Objekt angesehen werden.
• In einer monoidalen Kategorie lässt sich der Begriff des Monoid-Objekts definieren, der den des Monoids verallgemeinert.

Beispiele

Jede Kategorie, die endliche Produkte und ein Endobjekt enthält, kann als symmetrisch monoidale Kategorie betrachtet werden: Der zweistellige Funktor wird durch eine natürliche Auswahl von Produkten definiert und das Endobjekt ist das Einheitsobjekt. Analog können wir als zweistelligen Funktor ein Koprodukt und als Einheitsobjekt ein Anfangsobjekt wählen.

Wir zeigen nun parallel die Struktur zweier solcher monoidaler Kategorien:

${\displaystyle R}$-Mod	Set
Für einen kommutativen Ring ${\displaystyle R}$ ist die Kategorie ${\displaystyle R}$-Mod der ${\displaystyle R}$-Moduln eine symmetrische monoidale Kategorie mit Produkt ${\displaystyle \otimes }$ (dem Tensorprodukt) und Einheit ${\displaystyle R}$.	Die Kategorie Set ist symmetrisch monoidal mit Produkt ${\displaystyle \times }$ und Einheit ${\displaystyle \{*\}}$.
Eine unitäre assoziative Algebra ist ein Objekt von ${\displaystyle R}$-Mod zusammen mit Pfeilen ${\displaystyle \nabla \colon A\otimes A\to A}$ und ${\displaystyle \eta \colon R\rightarrow A}$, für die folgende Diagramme kommutieren:	Ein Monoid ist ein Objekt M zusammen mit Pfeilen ${\displaystyle \circ \colon M\times M\rightarrow M}$ und ${\displaystyle 1\colon \{*\}\to M}$, für die folgende Diagramme kommutieren:
und	und
Eine Koalgebra ist ein Objekt C mit Pfeilen ${\displaystyle \Delta \colon C\to C\otimes C}$ und ${\displaystyle \varepsilon \colon C\to R}$, für die folgende Diagramme kommutieren:	Zu jedem Objekt S in der Kategorie Set gibt es zwei eindeutig bestimmte Pfeile ${\displaystyle \Delta \colon S\to S\times S}$ und ${\displaystyle \varepsilon \colon S\to \{*\}}$, für die folgende Diagramme kommutieren:
und	und
	Insbesondere ist ${\displaystyle \varepsilon }$ eindeutig, weil ${\displaystyle \{*\}}$ Endobjekt ist.

Quellen

• Joyal, André; Street, Ross (1993). "Braided Tensor Categories". Advances in Mathematics 102, 20–78.
• Mac Lane, Saunders (1997), Categories for the Working Mathematician (2nd ed.). New York: Springer-Verlag.

V

Kategorientheorie

Einordnung	Typen von Kategorien dual | diskret | klein | lokal klein | monoidal | symmetrisch monoidal | angereichert | ausgeglichen | erreichbar | vollständig | kovollständig Typen von Objekten initial | terminal | null | injektiv | projektiv | Generator | Kogenerator | Pro | Ind | Gruppe | Monoid | exponential | frei | kompakt Typen von Morphismen Mono | Epi | Bi | Retraktion | Koretraktion | Injektive Auflösung | Projektive Auflösung Typen von Funktoren konstant | voll | treu | volltreu | additiv | exakt | abgeleitet | glatt
Konstruktionen	Limes Produkt | Differenzkern | Faserprodukt | Ende Kolimes Filtrierter Kolimes | Koprodukt | Differenzkokern | Kofaserprodukt Kan-Erweiterung | Monade | Komonade | Kategorie der Elemente | Kommakategorie | Pfeilkategorie | Homotopie-Kategorie
Resultate	Lemma von Yoneda | Fixpunktsatz von Lawvere | Einbettungssatz von Mitchell
Spezielle Funktoren	Hom-Funktor | Potenzmengenfunktor | Diagonalfunktor | Ext | Tor