|
Monade (Kategorientheorie) Eine Monade ist im mathematischen Teilgebiet der Kategorientheorie eine Struktur, die gewisse formale Ähnlichkeit mit den Monoiden der Algebra aufweist.
Definition
Eine Monade ist ein Tripel  aus aus
- einem Funktor
 von einer Kategorie von einer Kategorie  in sich selbst, das heißt in sich selbst, das heißt

- einer natürlichen Transformation
 (dabei steht (dabei steht  für den Identitätsfunktor für den Identitätsfunktor  ) )
- einer natürlichen Transformation
 (dabei steht (dabei steht  für für  ), ),
so dass die folgenden Bedingungen, die man auch die Axiome der Monade nennt, erfüllt sind:
 , das heißt das folgende Diagramm kommutiert: , das heißt das folgende Diagramm kommutiert:

 , das heißt das folgende Diagramm kommutiert: , das heißt das folgende Diagramm kommutiert:

Explizit bedeutet die Kommutativität der Diagramme, dass für jedes Objekt  in in  die beiden Diagramme die beiden Diagramme
 und und 
kommutieren.
Dabei sind  und und  die durch die durch  und und  definierten natürlichen Transformationen, entsprechendes gilt für definierten natürlichen Transformationen, entsprechendes gilt für  und und  .
Die natürlichen Transformationen .
Die natürlichen Transformationen  und und  nennt man auch Einheit und Multiplikation der Monade.[1][2] nennt man auch Einheit und Multiplikation der Monade.[1][2]
Beispiel Listen
Ein Beispiel für eine Monade sind Listen. Es bezeichne ![{\displaystyle [x_{1},\dotsc ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06f947669a99c7b06aca52887ca4aaa7f75967aa) die Liste mit den Elementen die Liste mit den Elementen  bis bis  , wobei mit , wobei mit  auch die leere Liste zugelassen ist. Listen sind Tupel, die wir hier der Übersichtlichkeit wegen mit eckigen Klammen schreiben. Das folgende Tripel auch die leere Liste zugelassen ist. Listen sind Tupel, die wir hier der Übersichtlichkeit wegen mit eckigen Klammen schreiben. Das folgende Tripel  ist eine Monade in der Kategorie der Mengen ist eine Monade in der Kategorie der Mengen  : :
Der Listen-Funktor
- Für ein Objekt
 aus aus  , das heißt für eine Menge , das heißt für eine Menge  , sei , sei ![{\displaystyle T(X)=\{[x_{1},\dotsc ,x_{n}]\mid n\in \mathbb {N} ,x_{1},\dotsc ,x_{n}\in X\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3cf06ba6bac7b5818e01d71efc8f8154d85f268) die Menge aller endlichen Listen, deren Elemente aus die Menge aller endlichen Listen, deren Elemente aus  kommen. kommen.
- Für eine Abbildung
 zwischen zwei Mengen sei zwischen zwei Mengen sei  zwischen den Listenmengen durch zwischen den Listenmengen durch ![{\displaystyle T(f)([x_{1},\dotsc ,x_{n}])=[f(x_{1}),\dotsc ,f(x_{n})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2dc4c74911b80f4d02d08282e907362114e849) definiert. definiert.
Einheit und Multiplikation
- Die Einheit
 sei definiert durch sei definiert durch ![{\displaystyle \eta _{X}(x)=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12e012aed242178cd2be2a1648f8a3fb27001e29) , das ist die Konstruktion einelementiger Listen. , das ist die Konstruktion einelementiger Listen.
- Die Multiplikation ist die Konkatenation von Listen:
![{\displaystyle \mu _{X}([l_{1},\dotsc ,l_{n}])=l_{1}\dotsm l_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7c497c74c69c13700e8714f28a14b45eb26f079) , also , also ![{\displaystyle \mu _{X}([[x_{11},\dotsc ,x_{1m_{1}}],\dotsc ,[x_{n1},\dotsc ,x_{nm_{n}}]])=[x_{11},\dotsc ,x_{1m_{1}},\dotsc ,x_{n1},\dotsc ,x_{nm_{n}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7520808b743d6e349608fb46396f95c4c58e6d9) – dies ist gewissermaßen das (einstufige) Zusammenfügen einer Liste von Listen zu einer Liste. – dies ist gewissermaßen das (einstufige) Zusammenfügen einer Liste von Listen zu einer Liste.
Diese Daten erfüllen die Definition der Monade.
- Die Gleichung
 bedeutet für eine Liste von Listen von Listen bedeutet für eine Liste von Listen von Listen  , dass , dass  , das heißt, dass es bei mehrfach verschachtelten Listen egal ist, ob diese von innen oder von außen beginnend zu einer zusammengefügt werden. Betrachte zum Beispiel , das heißt, dass es bei mehrfach verschachtelten Listen egal ist, ob diese von innen oder von außen beginnend zu einer zusammengefügt werden. Betrachte zum Beispiel ![{\displaystyle l=[[[x,y],[x]],[[x,y,z],[x,x]]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f79361626ed82dc71a3f2fb56e36b14148bd0d2d) , wobei , wobei  seien. Das ist die Liste der beiden Listen von Listen seien. Das ist die Liste der beiden Listen von Listen ![{\displaystyle [[x,y],[x]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21838dc13b7b2de0ac4b2fdcf2ba2a4536cc3d80) und und ![{\displaystyle [[x,y,z],[x,x]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4ebd48c74b690f358877d3bb73dcdc6b2b684ad) , die ihrerseits aus den Listen , die ihrerseits aus den Listen ![{\displaystyle [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663) und und ![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d) bzw. bzw. ![{\displaystyle [x,y,z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af0bfedf9a4341d42ead3affff487ec9debd8365) und und ![{\displaystyle [x,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bd63d788d7e9c6c0aff897a7906cda81e14c9cd) bestehen. Dann ist bestehen. Dann ist
![{\displaystyle \mu _{X}(T(\mu _{X})(l))=\mu _{X}([[x,y,x],[x,y,z,x,x]])=[x,y,x,x,y,z,x,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5aede91ca384d5f70807e29823a0365078e35379) und und![{\displaystyle \mu _{X}(\mu _{T(X)}(l))=\mu _{X}([[x,y],[x],[x,y,z],[x,x]])=[x,y,x,x,y,z,x,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1bf94ed735e797accfb88ca400862b19e6743db) . .
- Das zweite Axiom besagt in diesem Beispiel, dass jede Liste durch Zusammenfügen einelementiger Listen entsteht:
![{\displaystyle \mu _{X}(\eta _{T(X)}([x_{1},\dotsc ,x_{n}]))=\mu _{X}([[x_{1},\dotsc ,x_{n}]])=[x_{1},\dotsc ,x_{n}]=\mu _{X}([[x_{1}],\dotsc ,[x_{n}]])=\mu _{X}(T(\eta _{X})([x_{1},\dotsc ,x_{n}]))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d14386d1ddadf215c5c53afcfd136cef69e9afb) . .
In einer algebraischen Sichtweise ist  die unterliegende Menge des freien Monoids über die unterliegende Menge des freien Monoids über  . Die Einheit . Die Einheit  bettet das Erzeugendensystem in den Monoid ein, die Multiplikation bettet das Erzeugendensystem in den Monoid ein, die Multiplikation  ist die Monoidmultiplikation. ist die Monoidmultiplikation.
Eilenberg-Moore-Algebren
Ist  eine Monade, so ist ein Paar eine Monade, so ist ein Paar  eine Eilenberg-Moore-Algebra (auch einfach nur Algebra genannt) für diese Monade, wenn die Gleichungen eine Eilenberg-Moore-Algebra (auch einfach nur Algebra genannt) für diese Monade, wenn die Gleichungen
 und und
gelten, das heißt, wenn die folgenden beiden Diagramme kommutieren:

Ein Homomorphismus von  nach nach  ist ein Pfeil ist ein Pfeil  in in  mit mit  , das heißt, dass nachstehendes Diagramm kommutiert: , das heißt, dass nachstehendes Diagramm kommutiert:

Für beliebige Objekte  aus aus  ist daher z. B. ist daher z. B.  eine Algebra, und eine Algebra, und  ist ein Homomorphismus von ist ein Homomorphismus von  nach nach  . Im obigen Beispiel der Listen sind die Algebren . Im obigen Beispiel der Listen sind die Algebren  genau die Monoide genau die Monoide  und und  multipliziert alle Elemente der Liste. multipliziert alle Elemente der Liste.
Die Eilenberg-Moore-Algebren zur Monade  bilden mit den angegebenen Homomorphismen eine Kategorie, die man die Kategorie der bilden mit den angegebenen Homomorphismen eine Kategorie, die man die Kategorie der  -Algebren nennt und mit -Algebren nennt und mit  bezeichnet.[3]
Im Falle der Listen-Monade bezeichnet.[3]
Im Falle der Listen-Monade  ist also ist also  die Kategorie der Monoide. die Kategorie der Monoide.
Weitere Beispiele
Linearkombinationen
Es sei  ein Körper. Legt man für Mengen ein Körper. Legt man für Mengen  fest, dass fest, dass  sei, also (eine Kodierung für) die Menge der formalen sei, also (eine Kodierung für) die Menge der formalen  -Linearkombinationen von Elementen von -Linearkombinationen von Elementen von  , lässt sich , lässt sich  als Objektabbildung eines Funktors als Objektabbildung eines Funktors  auffassen, dessen Pfeilabbildung einer Funktion auffassen, dessen Pfeilabbildung einer Funktion  die Funktion die Funktion  , mit , mit  , zuordnet. , zuordnet.
 trägt eine naheliegende Vektorraumstruktur: Für trägt eine naheliegende Vektorraumstruktur: Für  und und  ist ist  , definiert durch , definiert durch  , wieder Element von , wieder Element von  , und für , und für  ist ist  , definiert durch , definiert durch  , ebenfalls wieder Element von , ebenfalls wieder Element von  . .
Der Funktor  wird zusammen mit den Festlegungen wird zusammen mit den Festlegungen
 
- (hier verwenden wir der Übersichtlichkeit halber
 und und  aus dem vorangegangenen Satz) aus dem vorangegangenen Satz)
zu einer Monade  . .  berechnet dabei auf naheliegende Weise aus einer Linearkombination von Linearkombinationen von Elementen von berechnet dabei auf naheliegende Weise aus einer Linearkombination von Linearkombinationen von Elementen von  die entsprechende Zusammenfassung als Linearkombination von Elementen von die entsprechende Zusammenfassung als Linearkombination von Elementen von  . .
Die Algebren der Monade  sind gerade sind gerade  -Vektorräume, in der zur Monade gehörenden Kleisli-Kategorie sind die Pfeile -Vektorräume, in der zur Monade gehörenden Kleisli-Kategorie sind die Pfeile  gerade (Mengen-indizierte) gerade (Mengen-indizierte)  - - -Matrizen, die sich als Codes für lineare Abbildungen vom freien Vektorraum über -Matrizen, die sich als Codes für lineare Abbildungen vom freien Vektorraum über  zum freien Vektorraum über zum freien Vektorraum über  auffassen lassen. auffassen lassen.
Dcpos
Der Endofunktor  auf der Kategorie der partiell geordneten Mengen und monotonen Abbildungen ordne jedem auf der Kategorie der partiell geordneten Mengen und monotonen Abbildungen ordne jedem  die partiell geordnete Menge die partiell geordnete Menge  der Ordnungsideale in der Ordnungsideale in  zu.
Seine Wirkung auf monotonen Abbildungen zu.
Seine Wirkung auf monotonen Abbildungen  sei sei  . Für eine partiell geordnete Menge . Für eine partiell geordnete Menge  und eine Teilmenge und eine Teilmenge  ist hierbei ist hierbei  . .
Die Abbildungsfamilien  und und  ergänzen den Funktor ergänzen den Funktor  zu einer Monade. zu einer Monade.
Die Strukturabbildung  einer einer  -Algebra -Algebra  ist nun gerade ist nun gerade  .
Jedes Ideal in .
Jedes Ideal in  (und somit jede gerichtete Teilmenge) hat also ein Supremum in (und somit jede gerichtete Teilmenge) hat also ein Supremum in  . Das heißt, eine . Das heißt, eine  -Algebra ist dasselbe wie eine Dcpo.
Ein Homomorphismus von -Algebra ist dasselbe wie eine Dcpo.
Ein Homomorphismus von  -Algebren ist eine Scott-stetige Abbildung. -Algebren ist eine Scott-stetige Abbildung.
Adjungierte Funktoren
Ist ein Funktor  zu einem Funktor zu einem Funktor  linksadjungiert, und sind linksadjungiert, und sind
 bzw. bzw. 
Einheit bzw. Koeinheit der Adjunktion, so ist  mit mit
  also also  für Objekte für Objekte 
eine Monade.
Dies ist im gewissen Sinn auch schon das einzige Beispiel, da jede Monade auf diese Weise entsteht, jedenfalls bis auf Isomorphie:
Die Tripel  mit mit  , ,  , ,  und und  sind Objekte einer Kategorie sind Objekte einer Kategorie  . In dieser Kategorie ist ein Morphismus von . In dieser Kategorie ist ein Morphismus von  nach nach  ein Funktor ein Funktor  , für den , für den  und und  gelten. gelten.

Anfangsobjekt in  ist ist  , wobei , wobei  die Kleisli-Kategorie zu die Kleisli-Kategorie zu  ist. ist.
 , für , für  ist ist  . .
 , für , für  ist ist  . .
Endobjekt in  ist ist  wobei wobei  die Kategorie der Eilenberg-Moore-Algebren zu die Kategorie der Eilenberg-Moore-Algebren zu  ist. ist.
 , für , für  ist ist  . .
 , ,  .[4] .[4]
Für eine vorgegebene Adjunktion  gibt es daher eindeutig existierende Funktoren gibt es daher eindeutig existierende Funktoren  und und  wie im nachfolgenden Diagramm, so dass die oben genannten Gleichungen bestehen, das heißt wie im nachfolgenden Diagramm, so dass die oben genannten Gleichungen bestehen, das heißt  , ,  , ,  und und 
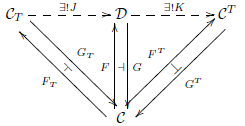
Den Funktor  nennt man auch den Vergleichsfunktor, weil der die Kategorie nennt man auch den Vergleichsfunktor, weil der die Kategorie  mit einer Kategorie von Algebren vergleicht.
Man nennt die Adjunktion mit einer Kategorie von Algebren vergleicht.
Man nennt die Adjunktion  monadisch, wenn der Vergleichsfunktor eine Äquivalenz monadisch, wenn der Vergleichsfunktor eine Äquivalenz  ist. Man nennt einen Funktor ist. Man nennt einen Funktor  monadisch, wenn es eine Linksadjungierte monadisch, wenn es eine Linksadjungierte  gibt, so dass die Adjunktion gibt, so dass die Adjunktion  monadisch ist. monadisch ist.
Monaden werden in der Informatik, besonders in funktionalen Programmiersprachen u. a. zur Abstraktion von Nebeneffekten verwendet. Es ist Haskell hervorzuheben, wo Monaden zur Integration von Ein- und Ausgabe in die sonst komplett von Seiteneffekten freie Sprache verwendet werden. Siehe dazu auch Monade (Informatik).
Weblinks
Einzelnachweise
- ↑ Saunders Mac Lane, Categories for the Working Mathematician. Springer-Verlag, Berlin 1971, ISBN 3-540-90035-7, Kap. VI.1 Monads in a Category, Definition auf S. 137
- ↑ Emily Riehl: Category Theory in Context. AMS Dover Publications, 2016, ISBN 978-0-486-80903-8, Definition 5.1.1, S. 154.
- ↑ Saunders Mac Lane, Categories for the Working Mathematician. Springer-Verlag, Berlin 1971, ISBN 3-540-90035-7, Kap. VI.1 Algebras for a Monad, Definition auf S. 140
- ↑ Emily Riehl: Category Theory in Context. AMS Dover Publications, 2016, ISBN 978-0-486-80903-8, Satz 5.2.12, S. 164.
|

























![{\displaystyle [x_{1},\dotsc ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06f947669a99c7b06aca52887ca4aaa7f75967aa)




![{\displaystyle T(X)=\{[x_{1},\dotsc ,x_{n}]\mid n\in \mathbb {N} ,x_{1},\dotsc ,x_{n}\in X\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3cf06ba6bac7b5818e01d71efc8f8154d85f268)


![{\displaystyle T(f)([x_{1},\dotsc ,x_{n}])=[f(x_{1}),\dotsc ,f(x_{n})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2dc4c74911b80f4d02d08282e907362114e849)
![{\displaystyle \eta _{X}(x)=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12e012aed242178cd2be2a1648f8a3fb27001e29)
![{\displaystyle \mu _{X}([l_{1},\dotsc ,l_{n}])=l_{1}\dotsm l_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7c497c74c69c13700e8714f28a14b45eb26f079)
![{\displaystyle \mu _{X}([[x_{11},\dotsc ,x_{1m_{1}}],\dotsc ,[x_{n1},\dotsc ,x_{nm_{n}}]])=[x_{11},\dotsc ,x_{1m_{1}},\dotsc ,x_{n1},\dotsc ,x_{nm_{n}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7520808b743d6e349608fb46396f95c4c58e6d9)


![{\displaystyle l=[[[x,y],[x]],[[x,y,z],[x,x]]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f79361626ed82dc71a3f2fb56e36b14148bd0d2d)

![{\displaystyle [[x,y],[x]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21838dc13b7b2de0ac4b2fdcf2ba2a4536cc3d80)
![{\displaystyle [[x,y,z],[x,x]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4ebd48c74b690f358877d3bb73dcdc6b2b684ad)
![{\displaystyle [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663)
![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
![{\displaystyle [x,y,z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af0bfedf9a4341d42ead3affff487ec9debd8365)
![{\displaystyle [x,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bd63d788d7e9c6c0aff897a7906cda81e14c9cd)
![{\displaystyle \mu _{X}(T(\mu _{X})(l))=\mu _{X}([[x,y,x],[x,y,z,x,x]])=[x,y,x,x,y,z,x,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5aede91ca384d5f70807e29823a0365078e35379)
![{\displaystyle \mu _{X}(\mu _{T(X)}(l))=\mu _{X}([[x,y],[x],[x,y,z],[x,x]])=[x,y,x,x,y,z,x,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1bf94ed735e797accfb88ca400862b19e6743db)
![{\displaystyle \mu _{X}(\eta _{T(X)}([x_{1},\dotsc ,x_{n}]))=\mu _{X}([[x_{1},\dotsc ,x_{n}]])=[x_{1},\dotsc ,x_{n}]=\mu _{X}([[x_{1}],\dotsc ,[x_{n}]])=\mu _{X}(T(\eta _{X})([x_{1},\dotsc ,x_{n}]))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d14386d1ddadf215c5c53afcfd136cef69e9afb)






























































































