Número do mal


mal
odioso
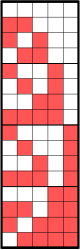
Os primeiros 16 números do mal e de ódio em binário little-endian. Pode-se ver que ambas as sequências diferem apenas nos bits menos significativos, que formam a sequência de Thue-Morse para o mal, e sua negação para os números odiosos. Os outros bits formam os números pares.

Em teoria dos números, um número do mal é um número inteiro não-negativo que possui um número par de dígitos 1 em sua representação binária.[1] Esses números fornecem as posições dos valores zero na sequência de Thue-Morse, e por esta razão também foram chamados de conjunto de Thue-Morse.[2] Inteiros não negativos que não são maus são chamados de número do ódio.

Exemplos

Os primeiros números do mal são:

0, 3, 5, 6, 9, 10, 12, 15, 17, 18, 20, 23, 24, 27, 29, 30, 33, 34, 36, 39...[1]

Somas iguais

A partição dos inteiros não negativos em números do ódio e do mal é a partição única desses números em dois conjuntos que possuem multiconjuntos iguais de somas aos pares.[3]

Como mostrou o matemático do século XIX, Eugène Prouhet, a divisão em números maus e odiosos dos números de para , para qualquer , fornece uma solução para o problema de Prouhet-Tarry-Escott de encontrar conjuntos de números cujas somas de potências são iguais até a potência .[4]

Referências

  1. ↑ a b Sloane, N. J. A. (ed.), «Sequência A001969 (Evil numbers: numbers with an even number of 1's in their binary expansion)», On-Line Encyclopedia of Integer Sequences (em inglês), OEIS Foundation 
  2. ↑ Charlier, Émilie; Cisternino, Célia; Massuir, Adeline (2019), «State complexity of the multiples of the Thue-Morse set», Proceedings Tenth International Symposium on Games, Automata, Logics, and Formal Verification, Electron. Proc. Theor. Comput. Sci. (EPTCS) (em inglês), 305, pp. 34–49, MR 4030092, arXiv:1903.06114Acessível livremente, doi:10.4204/EPTCS.305.3Acessível livremente 
  3. ↑ Lambek, J.; Moser, L. (1959), «On some two way classifications of integers», Canadian Mathematical Bulletin (em inglês), 2 (2): 85–89, MR 104631, doi:10.4153/CMB-1959-013-xAcessível livremente 
  4. ↑ Wright, E. M. (1959), «Prouhet's 1851 solution of the Tarry-Escott problem of 1910», American Mathematical Monthly (em inglês), 66 (3): 199–201, JSTOR 2309513, MR 104622, doi:10.2307/2309513