多面体トーラスはトーラス曲面の近似として、四辺形面からなる展開図から、構成することができる。この例では 6×4 個の面をもつ
初等幾何学における穿孔多面体（せんこうためんたい、英: toroidal polyhedron; トーラス形多面体[1], 環状多面体）は、位相的にトーラス型立体（種数 g が 1 またはそれ以上のトーラス）であるような多面体を言う。通常の多面体が多角形による球面の充填であるのに対し、穿孔多面体はトーラス（あるいは多孔トーラス）の充填であり、貫通した孔を持つ。
重要な例にチャーサールの多面体（英語版）（チャーサールの環状十四面体）およびシラッシの多面体（シラッシの環状七面体）がある。
穿孔多面体は必ず凹多面体である。また、オイラー標数が孔のない多面体のように2にはならない。一般に、孔が n 個ある穿孔多面体のオイラー標数は、2 (1 - n) である。
チャーサールの多面体
シラッシの多面体
種々の定義
穿孔多面体は、辺および頂点でのみ交わるような多角形の族で、それら自身がひとつの多様体を成すようなものとして定義できる。すなわち、各辺はちょうど二つの多角形に共有されなければならず、また各頂点のリンク（英語版）は辺とその頂点に接続する多角形の間を行き来する単一の閉路でなければならない。穿孔多面体に対し、それを多様体と見れば向き付け可能な曲面である[2]。文献によっては、"toroidal polyhedra"（トロイダル多面体、トーラス形多面体）の語が、より特定の位相的に種数 1 のトーラスと同値であるような多面体の意味で用いられる[3]
この分野では、埋め込み穿孔多面体（それは、三次元ユークリッド空間における平坦多角形を面とし、それら面は互いにあるいはそれ自身と交差することはない）。を抽象多面体（英語版）（如何なる特定の幾何学的実現も持たない位相的曲面）と区別することが重要である[4]。これら二つの極端な例の間には、ユークリッド空間内の多角形または星型多角形によって幾何学的に実現されるはめ込み穿孔多様体があり、それはそれら多角形が互いに交わることを許す。
これらすべての場合において、多面体がトーラス形であるという特質はその向き付け可能性およびオイラー標数が非正であることによって確かめられる。
チャーサールとシラッシの多面体
もっとも単純な埋め込み穿孔多面体の二つがチャーサールの多面体とシラッシの多面体である。
チャーサールの多面体（英語版）は、七頂点の穿孔多面体で、21の辺と14の三角形面を持つ[5]。これと四面体の二つのみが、任意の二頂点を結ぶ線分が必ずその多面体の辺となっているような多面体であると知られている[6]。
チャーサールの多面体の双対がシラッシの多面体であり、それは七つの六角形面がどの二つも互いに隣接 (adjacent) する多面体である[7]。したがって、それは（種数 1 の）トーラス上の地図の彩色に必要な色の最大数が七色であるという定理の半分、存在性を提供する[8]。
チャーサールの多面体は任意の埋め込み穿孔多面体の中で可能な最小の頂点数をもち、またシラッシの多面体は任意の埋め込み穿孔多面体の中で可能な最小の面数を持つ。
スチュワートの環形体
穿孔多面体の特別なクラスとして、正多角形面で囲まれた、自己交叉を持たない多面体で、更なる制約としてどの隣り合う面も同一面上にないという条件を課したものを、それらを集中的に研究したボニー・スチュワート（英語版） の名に因んで、スチュワートのトーラス形 (Stewart toroid) と呼ぶ[10]。これは凸多面体の場合のジョンソンの立体に対応するものだが、ジョンソンの立体と異なり、スチュワートのトーラス形は無限個存在する。その中には、トーラスデルタ多面体（すべての面が等辺三角形であるような多面体）が含まれる。
スチュワートのトーラス形を制限したクラスとして、これもやはりスチュワートが定義したものだが、準凸穿孔多面体 (quasi-convex toroidal polyhedra) がある。これは、その多面体の凸包の辺が全てもともとの多面体の辺であるようなスチュワートのトーラス形である。そのような多面体に対し、凸包の各面はもとのトーラス形の面となることもあれば、トーラス形の面上に全ての辺が載った多角形となることもある[12]。
単一の多面体の張り合わせであるようなスチュワートのトーラス形
| 種数 |
1 |
1
|
| 像
|
|
|
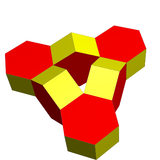
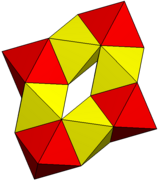
| 成分多面体
|
六つの六角柱
|
八つの八面体
|
| 頂点数
|
48 |
24
|
| 辺数
|
84 |
72
|
| 面数
|
36 |
48
|
混成張り合わせで得られるスチワートのトーラス形
| 種数 |
1 |
3 |
11 |
3 |
5 |
7 |
11
|
| 像
|
|
|
|
|
|
|
|
|
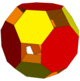
| 成分多面体
|
四角台塔 × 4; 四面体 × 8
|
三角台塔 × 6; 四角柱 × 6
|
三角台塔 × 4; 四角柱 × 6
|
三角柱 × 24; 四角柱 × 6; 四面体 × 8
|
|
|
|
|
| 頂点数
|
32 |
30 |
30 |
62 |
|
|
|
|
| 辺数
|
64 |
60 |
72 |
168 |
|
|
|
|
| 面数
|
32 |
30 |
38 |
86 |
|
|
|
|
はめ込まれた多面体
空間における交叉多角形の族によって形作られる多面体は、それら多角形および共有する辺および頂点の族によって得られる抽象位相多様体の多角形はめ込みである。例として、種数 1 の八面半八面体、種数 3 の小立方立方八面体および種数 4 の大十二面体が挙げられる。
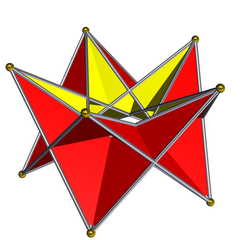五角ステファン多面体: このステファン多面体は五角形の二面体群対称性を持ち、またその頂点集合は一様五角柱と同一である。
王冠型多面体 (crown polyhedron) あるいはステファン多面体 (stephanoid) は、ノーブル多面体（英語版）（同角（英語版）かつ同面（英語版））でもある穿孔多面体を言う。この多面体は自己交叉を持ち、かつ位相的に自己双対（英語版）である[13]。
注
注釈
出典
- ^ 宮崎興二『多面体百科』丸善出版
- ^ Whiteley (1979); Stewart (1980), p. 15.
- ^ Webber, William T. (1997), “Monohedral idemvalent polyhedra that are toroids”, Geometriae Dedicata 67 (1): 31–44, doi:10.1023/A:1004997029852, MR1468859 .
- ^ Whiteley, Walter (1979), “Realizability of polyhedra”, Structural Topology (1): 46–58, 73, MR621628, http://www.iri.upc.edu/people/ros/StructuralTopology/ST1/st1-07-a4.pdf .
- ^ Császár, A. (1949), “A polyhedron without diagonals”, Acta Sci. Math. Szeged 13: 140–142 .
- ^ Ziegler, Günter M. (2008), “Polyhedral Surfaces of High Genus”, in Bobenko, A. I.; Schröder, P.; Sullivan, J. M. et al., Discrete Differential Geometry, Oberwolfach Seminars, 38, Springer-Verlag, pp. 191–213, arXiv:math.MG/0412093, doi:10.1007/978-3-7643-8621-4_10, ISBN 978-3-7643-8620-7 .
- ^ Szilassi, Lajos (1986), “Regular toroids”, Structural Topology 13: 69–80, http://haydn.upc.es/people/ros/StructuralTopology/ST13/st13-06-a3-ocr.pdf .
- ^ Heawood, P. J. (1890), “Map colouring theorems”, Quarterly J. Math. Oxford Ser. 24: 322–339
- ^ Webb, Robert (2000), “Stella: polyhedron navigator”, Symmetry: Culture and Science 11 (1-4): 231–268, MR2001419, http://www.software3d.com/PolyNav/PolyNavigator.php .
- ^ Stewart 1980, pp. 76–79, "Quasi-convexity and weak quasi-convexity".
- ^ Grünbaum, Branko (1994), “Polyhedra with Hollow Faces”, Polytopes: Abstract, Convex and Computational, NATO ASI Series C: Mathematical and Physical Series, 440, Kluwer Academic Publishers, pp. 43–70, doi:10.1007/978-94-011-0924-6_3, https://books.google.com/books?id=gHjrCAAAQBAJ&pg=PA43 . See in particular p. 60.
参考文献
関連項目
外部リンク
