ja %E5%8D%8A%E6%AD%A3%E5%A4%9A%E9%9D%A2%E4%BD%93

半正多面体 (はんせいためんたい、semi-regular polyhedron) またはアルキメデスの立体 (Archimedean solid) とは、凸な一様多面体のうち、正多面体以外のものである。また、対称性が低い (Dihedral) 角柱・反角柱・ミラーの立体も除く。全部で13種類ある。

一様多面体の条件は、全ての面が正多角形で、頂点形状が合同（頂点に集まる正多角形の種類と順序が同じ）なことである。正多面体（別名：プラトンの立体）は除外するので、半正多面体の面は2種類以上の正多角形で構成される。

準正多面体 (quasi-regular polyhedron) とは、このうち辺の近傍が合同なもので、立方八面体と二十・十二面体が当てはまる。

semi-regular polyhedron のことを準正多面体ということがあるが、数学用語の一般的な訳し方に沿うなら semi-regular polyhedron は半正多面体、quasi-regular polyhedron は準正多面体である^[1]。

一覧

多面体	構成面	面	辺	頂点	頂点形状	双対
切頂四面体	正三角形 4枚正六角形 4枚	8	18	12	3,6,6	三方四面体
切頂六面体	正三角形 8枚正八角形 6枚	14	36	24	3,8,8	三方八面体
切頂八面体	正方形 6枚正六角形 8枚	14	36	24	4,6,6	四方六面体
切頂十二面体	正三角形 20枚正十角形 12枚	32	90	60	3,10,10	三方二十面体
切頂二十面体（サッカーボール型）	正五角形 12枚正六角形 20枚	32	90	60	5,6,6	五方十二面体
立方八面体	正三角形 8枚正方形 6枚	14	24	12	3,4,3,4	菱形十二面体
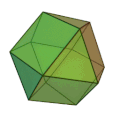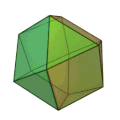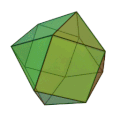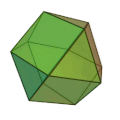
二十・十二面体	正三角形 20枚正五角形 12枚	32	60	30	3,5,3,5	菱形三十面体
斜方立方八面体	正三角形 8枚正方形 18枚	26	48	24	3,4,4,4	凧形二十四面体
斜方二十・十二面体	正三角形 20枚正方形 30枚正五角形 12枚	62	120	60	3,4,5,4	凧形六十面体
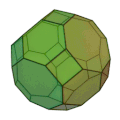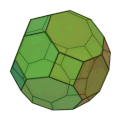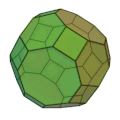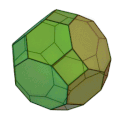
斜方切頂立方八面体	正方形 12枚正六角形 8枚正八角形 6枚	26	72	48	4,6,8	六方八面体
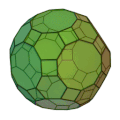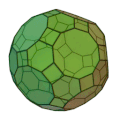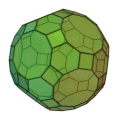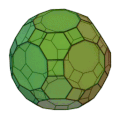
斜方切頂二十・十二面体	正方形 30枚正六角形 20枚正十角形 12枚	62	180	120	4,6,10	六方二十面体
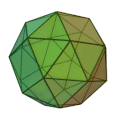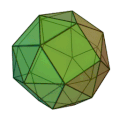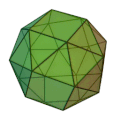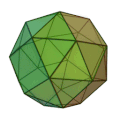
変形立方体（鏡像あり）	正三角形 32枚正方形 6枚	38	60	24	3,3,3,3,4	五角二十四面体
変形十二面体（鏡像あり）	正三角形 80枚正五角形 12枚	92	150	60	3,3,3,3,5	五角六十面体

半正多面体でない多面体

「面が正多角形で頂点形状が合同」という条件を満たすが、対称性が低いために半正多面体に含められない多面体に、ミラーの立体・アルキメデスの角柱・アルキメデスの反角柱がある。

ミラーの立体は、斜方立方八面体の上部三分の一を45度ひねった多面体である。頂点形状は合同であるが、対称性が2次元的で (D_4d)、頂点に関する推移性を満たさない。ただし、ミラーの立体を半正多面体に含め、キラルな変形立方体と変形十二面体の鏡像を区別し、半正多面体を16種類とする場合もある。^[2]

アルキメデスの正角柱とアルキメデスの反角柱を含めないのは、一般に対称性が2次元的であることの他、種類が無限にあることも理由である。アルキメデスの立体と言った場合は含むこともある。

正多面体からの作製

半正多面体は、正多面体のいずれかを削って作ると考えて、以下の5種類に分類することができる。^[3]

切頂 n 面体: 正 n 面体の頂点まわりを切頂したもの。切隅 n 面体、切頭 n 面体とも。拡張シュレーフリ記号は t{p, q}
n・m 面体（準正多面体）: 正 n または m 面体の頂点まわりを各辺の中点まで切ったもの。拡張シュレーフリ記号は ${\begin{Bmatrix}p\\q\end{Bmatrix}}$
斜方 n・m 面体: 正 n または m 面体の各辺まわりの切稜と頂点まわりの切頂を組み合わせたもの。そのうち切頂面が正三角形のものを指す。小斜方 n・m 面体、（小）菱形 n・m 面体とも。拡張シュレーフリ記号は $r{\begin{Bmatrix}p\\q\end{Bmatrix}}$
斜方切頂 n・m 面体: 正 n または m 面体の各辺まわりの切稜と頂点まわりの切頂を組み合わせたもの。そのうち切頂面が正六角形のものを指す。; 大斜方 n・m 面体、大菱形 n・m 面体とも。拡張シュレーフリ記号は $t{\begin{Bmatrix}p\\q\end{Bmatrix}}$; [注意] 「n・m 面体の頂点を切ったもの。切頂 n・m 面体」というような説明や理解も存在するが、準正多面体 n・m 面体を切頂した面は、正方形とはならず長方形となるので、誤りである。
変形 n 面体: 正 n 面体の面上に、縮小した各面を捩じって配置し、隣接する頂点が正三角形となるように切り取ったもの。鏡像がある。捩れ n 面体とも呼ばれる。拡張シュレーフリ記号は $s{\begin{Bmatrix}p\\q\end{Bmatrix}}$

双対

半正多面体の双対は、アルキメデス双対あるいはカタランの立体と呼ばれる。1種類の正多角形でない面からできており、すべての二面角は等しい。カタランの立体の面心（内接円の中心）を頂点とする立体は半正多面体であるが、半正多面体の面心を頂点とする立体がカタランの立体となるわけではない。

出典

^ コラム第７回自分で自分の首を絞めた話～準正多面体と半正多面体～
^ 正多面体を解く. 東海大学出版会. (2002)
^ 正多面体を解く. 東海大学出版会. (2002/5/20)

[1] コラム第７回自分で自分の首を絞めた話～準正多面体と半正多面体～

[2] 正多面体を解く. 東海大学出版会. (2002)

[3] 正多面体を解く. 東海大学出版会. (2002/5/20)

[1]

[2]

[3]