Equazione di Debye-Hückel

Distribuzione degli ioni in una soluzione

I chimici Peter Debye ed Erich Hückel condussero studi sulle soluzioni che contengono soluti ionici e notarono un comportamento non ideale anche a concentrazioni molto basse. Quindi, mentre la concentrazione dei soluti è fondamentale per il calcolo della dinamica di una soluzione, essi teorizzarono un fattore aggiuntivo detto gamma per il calcolo del coefficiente di attività di un certo tipo di ione in soluzione. Questo porta a due equazioni: quella formulata da Debye–Hückel detta anche 'equazione di Debye–Hückel limitata o legge limite di Debye–Hückel e quella modificata empiricamente detta 'equazione di Debye–Hückel estesa. L'attività è solo proporzionale alla concentrazione e viene alterata tramite un fattore noto come coefficiente di attività ${\displaystyle \gamma }$. Tale fattore tiene conto dell'energia di interazione degli ioni presenti in soluzione.

Equazione di Debye–Hückel

Per i principi usati per derivare questa equazione vedi la teoria di Debye-Hückel

Il presupposto chiave è che lo ione centrale della nuvola sia una carica puntiforme e che gli altri ioni sono sparsi attorno allo ione centrale con una distribuzione di Boltzmann. Il suo campo d'applicazione è limitato a ${\displaystyle I<0,01M}$, il che significa che non è utile per l'acqua di mare.

Per poter calcolare l'attività ${\displaystyle a_{C}}$ di uno ione C in una soluzione, bisogna conoscere la concentrazione e il coefficiente di attività:

${\displaystyle a_{C}=\gamma {\frac {[C]}{[C^{\ominus }]}},}$

dove

Simbolo	Definizione
${\displaystyle \gamma }$	Il coefficiente di attività dello ione C
${\displaystyle [C^{\ominus }]}$	La concentrazione allo stato standard, ad esempio 1 mole/kg se usiamo la molalità,
${\displaystyle [C]}$	La concentrazione dello ione C

Dividendo ${\displaystyle [C]}$ con ${\displaystyle [C^{\ominus }]}$ si ottiene una quantità senza dimensione. Quindi ${\displaystyle a_{C}}$ è proporzionale al parametro ${\displaystyle \gamma }$.

La legge limite di Debye–Hückel permette di determinare il coefficiente di attività dello ione i-esimo in una soluzione diluita nota la forza ionica, cioè:[1]section 2.5.2

${\displaystyle \ln(\gamma _{i})=-{\frac {z_{i}^{2}q^{2}\kappa }{8\pi \varepsilon _{r}\varepsilon _{0}k_{B}T}}=-{\frac {z_{i}^{2}q^{3}N_{\text{A}}^{1/2}}{4\pi (\varepsilon _{r}\varepsilon _{0}k_{B}T)^{3/2}}}{\sqrt {10^{3}{\frac {I}{2}}}}}$

ottenendo le due espressioni comuni:

${\displaystyle \ln(\gamma _{i})=-Az_{i}^{2}{\sqrt {I}}\,}$

${\displaystyle \log _{10}(\gamma _{i})=-{\frac {A}{\ln 10}}z_{i}^{2}{\sqrt {I}}\,}$

dove

Simbolo	Definizione
${\displaystyle z_{i}}$	Numero di carica dello specifico ione i-esimo
${\displaystyle q}$	Carica elementare
${\displaystyle \kappa }$	Inverso della lunghezza preferita di Debye
${\displaystyle \varepsilon _{r}}$	La permittività relativa del solvente
${\displaystyle \varepsilon _{0}}$	La permittività dielettrica del vuoto
${\displaystyle k_{B}}$	La costante di Boltzmann
${\displaystyle T}$	La temperatura della soluzione
${\displaystyle N_{\mathrm {A} }}$	La costante di Avogadro
${\displaystyle I}$	La forza ionica della soluzione
${\displaystyle A}$	Una costante che dipende dalla temperatura. Se ${\displaystyle I}$ è espresso in termini di molalità, anziché di molarità

Se ${\displaystyle I}$ viene espresso in termini di molalità (come nell'equazione sopra e nel resto di questa voce), allora un valore sperimentale di ${\displaystyle A}$ per l'acqua è ${\displaystyle 1.172{\text{ mole}}^{-1/2}{\text{kg}}^{1/2}}$ a 25 °C. Nel caso di esprimi ${\displaystyle \gamma _{i}}$ con il logaritmo in base 10, allora (secondo la relazione del cambio di base) dobbiamo dividere per il fattore ${\displaystyle \ln 10}$, così A diventa ${\displaystyle 0.509{\text{ mole}}^{-1/2}{\text{kg}}^{1/2}}$.

È importante notare che poiché gli ioni nella soluzione agiscono insieme, il coefficiente di attività ottenuto da questa equazione è in realtà un coefficiente medio. Per una soluzione con un solo elettrolita (soluto) tale coefficiente di attività ionico medio ha l'espressione:

${\displaystyle \ \ln(\gamma _{\pm })=-A\,|z_{+}z_{-}|{\sqrt {I}}\,}$

${\displaystyle \ \log _{10}(\gamma _{\pm })=-{\frac {A}{\ln 10}}\,|z_{+}z_{-}|{\sqrt {I}}\,}$

La pressione osmotica in eccesso ricavata dalla teoria di Debye–Hückel si ottiene nelle unità cgs dalla:[2]

${\displaystyle P^{\text{ex}}=-{\frac {k_{B}T\kappa _{\text{cgs}}^{3}}{24\pi }}=-{\frac {k_{B}T\left({\frac {4\pi \sum _{j}c_{j}q_{j}}{\epsilon _{0}\epsilon _{r}k_{B}T}}\right)^{3/2}}{24\pi }}.}$

Pertanto, la pressione totale è la somma della pressione osmotica in eccesso e della pressione ideale ${\displaystyle P^{\text{id}}=k_{B}T\sum _{i}c_{i}}$. Il coefficiente osmotico diventa

${\displaystyle \phi ={\frac {P^{\text{id}}+P^{\text{ex}}}{P^{\text{id}}}}=1+{\frac {P^{\text{ex}}}{P^{\text{id}}}}.}$

Vedremo nel seguito l'altra equazione di Debye–Hückel detta estesa valida per soluzioni a forza ionica fino a ${\displaystyle I<0.1M}$, dove M indica la molarità.

Teoria degli elettroliti diluiti, Debye P. - Hückel E. (1923)

Il titolo inglese dell'articolo è On the Theory of Electrolytes. I. Freezing Point Depression and Related Phenomena. Fu pubblicato inizialmente nel 1923 nel volume 24 della rivista tedesca Physikalische Zeitschrift. Una traduzione inglese[3]pp. 217–263dell'articolo è incluso in un libro di raccolte presentato da Debye per i suoi allievi, amici ed editori in occasione del suo settantesimo compleanno il 24 marzo 1954.[3]vedi xv

Un'ulteriore traduzione di Michael J. Braus rileva diversi errori di traduzione e composizione nell'edizione del 1954 (InterScience Publishers, ora John Wiley & Sons), in particolare l'uso errato di ${\displaystyle \kappa }$ con ${\displaystyle x}$ che per gli autori era considerata la variabile più importante nel loro lavoro.[4] Il simbolo sbagliato ${\displaystyle \kappa }$ in tutta la letteratura della chimica fisica, è quello che denota la lunghezza Debye in soluzione elettrolita. L'articolo si occupa del calcolo delle proprietà delle soluzioni elettrolitiche che sono sotto l'influenza dei campi elettrici indotti dagli ioni, quindi nell'ambito dell'elettrostatica.

Nello stesso anno in cui pubblicarono per la prima volta il loro lavoro, Debye e Hückel, di seguito D&H, pubblicarono anche un secondo articolo che trattava la loro iniziale caratterizzazione di soluzioni sotto l'influenza di campi elettrici denominato On the Theory of Electrolytes. II. Limiting Law for Electric Conductivity[3]pp. 264–310, ma qui non viene trattato.

Nel seguente riassunto, incompleto e non aggiornato, vengono utilizzate notazioni e terminologie moderne, sia della chimica che della matematica, per evitare confusione. Inoltre, con alcune eccezioni per migliorare la chiarezza, le sottosezioni di questo riepilogo sono versioni ridotte di quelle originarie.

Coefficiente di attività stechiometrico e ionico medio

D&H notarono che la formula di Guldberg-Waage per le specie di elettroliti in una reazione chimica all'equilibrio nella forma classica è[3]p. 221

${\displaystyle \prod _{i=1}^{s}x_{i}^{\nu _{i}}=K,}$

dove

Simbolo	Definizione
${\displaystyle \textstyle \prod }$	Una notazione per la moltiplicazione
${\displaystyle i}$	Una variabile dummy per indicare uno specifico elettrolita (soluto)
${\displaystyle s}$	Il numero totale degli elettroliti (soluti) che partecipano alla reazione
${\displaystyle x_{i}}$	La frazione molare del soluto ${\displaystyle i}$-esimo
${\displaystyle \nu _{i}}$	Il coefficiente stechiometrico del soluto ${\displaystyle i}$-esimo
K	La costante di equilibrio

D&H affermarono che, a causa delle forze elettrostatiche reciproche tra gli ioni, è necessario modificare l'equazione di Guldberg-Waage sostituendo ${\displaystyle K}$ con ${\displaystyle \gamma K}$, dove ${\displaystyle \gamma }$ è un coefficiente di attività complessivo, non uno specifico coefficiente di attività (cioè il ${\displaystyle \gamma _{i}}$ associato a ciascun tipo di ione presente nella soluzione acquosa), detto coefficiente di attività stechiometrico e utilizzato nella chimica moderna a partire dal 2007. La relazione tra ${\displaystyle \gamma }$ e i coefficienti di attività della specie ionica ${\displaystyle \gamma _{i}}$ è[3]p. 248(la notazione ${\displaystyle \log }$ s'intende di solito il logaritmo in base 10):

${\displaystyle \log(\gamma )=\sum _{i=1}^{s}\nu _{i}\log(\gamma _{i}).}$

Il coefficiente di attività ionico medio si applica nel caso di soluti elettroliti completamente dissociati. La relazione tra ${\displaystyle \gamma _{\pm }}$ e i coefficienti di attività dei singoli ioni ${\displaystyle \gamma _{i}}$ è una media geometrica pesata dal numero cationi e anioni presenti nella formula del soluto elettrolita ì-esimo:

${\displaystyle \log(\gamma _{\pm })={\frac {1}{\displaystyle \sum _{i=1}^{s}\nu _{i}}}\,\sum _{i=1}^{s}\nu _{i}\log(\gamma _{i}).}$

L'energia interna U di una soluzione ionica

D&H usarono le entropie libere ${\displaystyle \Phi }$ di Helmholtz e ${\displaystyle \Xi }$ di Gibbs per esprimere l'effetto delle forze elettrostatiche in un elettrolita ad un certo stato termodinamico. In particolare, divisero la maggior parte del potenziale termodinamico, cioè il calcolo dell'energia ${\displaystyle U}$ della soluzione, nel termine classico ed elettrostatico:

${\displaystyle \Phi =S-{\frac {U}{T}}=-{\frac {A}{T}},}$

dove

Simbolo	Definizione
${\displaystyle \Phi }$	L'entropia libera di Helmholtz
${\displaystyle S}$	L'entropia
${\displaystyle U}$	L'energia interna
${\displaystyle T}$	La temperatura
${\displaystyle A}$	L'energia libera di Helmholtz

D&H esplicitarono il differenziale totale di ${\displaystyle \Phi }$ come[3]p. 222

${\displaystyle d\Phi ={\frac {P}{T}}\,dV+{\frac {U}{T^{2}}}\,dT,}$

dove

Simbolo	Definizione
${\displaystyle P}$	La pressione
${\displaystyle V}$	Il volume

Per definizione di differenziale totale, significa che

${\displaystyle {\frac {P}{T}}={\frac {\partial \Phi }{\partial V}},}$

${\displaystyle {\frac {U}{T^{2}}}={\frac {\partial \Phi }{\partial T}},}$

che sono utili più avanti.

Come affermato in precedenza, l'energia interna è divisa in due parti:[3]p. 222

${\displaystyle U=U_{k}+U_{e}}$

dove

Simbolo	Definizione
${\displaystyle k}$	Parte classica dell'energia interna
${\displaystyle e}$	Parte elettrica dell'energia interna

Analogamente, l'entropia libera di Helmholtz è divisa pure in due parti:

${\displaystyle \Phi =\Phi _{k}+\Phi _{e}.}$

D&H affermarono, senza darne la spiegazione logica[3]p. 222

${\displaystyle \Phi _{e}=\int {\frac {U_{e}}{T^{2}}}\,dT.}$

Sembrerebbe che quindi

${\displaystyle \Phi _{e}=\int {\frac {P_{e}}{T}}\,dV+\int {\frac {U_{e}}{T^{2}}}\,dT.}$

Senza menzionarlo in modo specifico, D&H in seguito fornirono quella che potrebbe essere la giustificazione di tali relazioni sostenendo che ${\displaystyle \Phi _{e}=\Xi _{e}}$, questo presuppone che il solvente sia incomprimibile.

La definizione dell'entropia libera di Gibbs ${\displaystyle \Xi }$ è[3]pp. 222–223

${\displaystyle \Xi =S-{\frac {U+PV}{T}}=\Phi -{\frac {PV}{T}}=-{\frac {G}{T}},}$

dove ${\displaystyle G}$ è l'energia libera di Gibbs.

D&H calcolarono il differenziale totale di ${\displaystyle \Xi }$ come[3]p. 222

${\displaystyle d\Xi =-{\frac {V}{T}}\,dP+{\frac {U+PV}{T^{2}}}\,dT.}$

A questo punto D&H notarono che, per acqua contenente 1 mole per litro di cloruro di potassio (non specificando la pressione nominale e la temperatura), la pressione elettrica ${\displaystyle P_{e}}$ ammonta a 20 atmosfere. Inoltre, notarono che questo livello di pressione dà una variazione di volume relativa di 0,001. Pertanto, trascurando il cambiamento in volume d'acqua per la pressione elettrica, scrissero[3]p. 223

${\displaystyle \Xi =\Xi _{k}+\Xi _{e},}$

e misero

${\displaystyle \Xi _{e}=\Phi _{e}=\int {\frac {U_{e}}{T^{2}}}\,dT.}$

D&H affermarono che, secondo Planck, la parte classica dell'entropia libera di Gibbs è[3]p. 223

${\displaystyle \Xi _{k}=\sum _{i=0}^{s}N_{i}(\xi _{i}-k_{B}ln(x_{i})),}$

dove

Simbolo	Definizione
${\displaystyle i}$	La specie chimica o soluto i-esimo
${\displaystyle s}$	Il numero di tipi differenti di particelle o soluti in soluzione
${\displaystyle N_{i}}$	Il numero di particelle del soluto i-esimo
${\displaystyle \xi _{i}}$	L'entropia libera di Gibbs specifica per la particella del soluto i-esimo
${\displaystyle k_{B}}$	La costante di Boltzmann
${\displaystyle x_{i}}$	La frazione molare del soluto i-esimo.

La specie per ${\displaystyle i=0}$ è il solvente. La definizione di ${\displaystyle \xi _{i}}$ è la seguente, dove le lettere minuscole indicano la particella specifica delle proprietà estensive corrispondenti:[3]p. 223

${\displaystyle \xi _{i}=s_{i}-{\frac {u_{i}+Pv_{i}}{T}}.}$

D&H non lo dicono, ma la forma funzionale per ${\displaystyle \Xi _{k}}$ può essere derivata dalla dipendenza del potenziale chimico di un componente di una soluzione ideale sulla sua frazione molare.[5]

D&H osservarono che l'energia interna ${\displaystyle U}$ di una soluzione è ridotta dall'interazione elettrica dei suoi ioni, ma che questo effetto non può essere determinato utilizzando l'approssimazione cristallografica per distanze tra atomi dissimili (la radice cubica del rapporto tra il volume totale e il numero di particelle nel volume). Questo perché c'è più movimento termico all'interno di una soluzione liquida che in un cristallo. Il movimento termico tende a modificare il reticolo naturale che altrimenti sarebbe costruito dagli ioni. Invece, D&H introducono il concetto di atmosfera ionica o nuvola. Come nel reticolo cristallino, ogni ione tenta ancora di circondare se stesso con ioni di carica opposta, ma in un modo più libero; a piccole distanze dagli ioni positivi, è più probabile trovare ioni negativi e viceversa.[3]p. 225

L'energia potenziale Ue di una soluzione ionica

La condizione di elettroneutralità di una soluzione richiede[3]p. 233

${\displaystyle \sum _{i=1}^{s}N_{i}z_{i}=0,}$

dove

Simbolo	Definizione
${\displaystyle N_{i}}$	Numero totale degli ioni del soluto i-esimo nella soluzione
${\displaystyle z_{i}}$	Il numero di carica del soluto i-esimo

Per portare uno ione della specie o soluto (elettrolita) i, inizialmente molto lontano, in un punto ${\displaystyle P}$ all'interno della nuvola di ioni occorre un'energia di interazione del valore di ${\displaystyle z_{i}q\varphi }$, dove ${\displaystyle q}$ è la carica elementare e ${\displaystyle \varphi }$ è il valore del campo scalare potenziale elettrico nel punto ${\displaystyle P}$. Se le forze elettriche fossero l'unico fattore in gioco, la configurazione a energia minima di tutti gli ioni raggiunge quella reticolare compatta. Tuttavia, gli ioni sono in equilibrio termico tra loro e sono relativamente liberi di muoversi. Quindi ubbidiscono alla statitstica di Boltzmann e formano una distribuzione di Boltzmann. Le densità numeriche di tutte le specie ${\displaystyle n_{i}}$ sono alterate dai loro valori generali (medi complessivi) ${\displaystyle n_{i}^{0}}$ dal corrispondente fattore di Boltzmann ${\displaystyle e^{-{\frac {z_{i}q\varphi }{k_{B}T}}}}$, dove ${\displaystyle k_{B}}$ è la costante di Boltzmann, e ${\displaystyle T}$ è la temperatura.[6] Così in ogni punto della nuvola ionica[3]p. 233:

${\displaystyle n_{i}={\frac {N_{i}}{V}}e^{-{\frac {z_{i}q\varphi }{k_{B}T}}}=n_{i}^{0}e^{-{\frac {z_{i}q\varphi }{k_{B}T}}}.}$

Si noti che nel limite di temperatura infinito, tutti gli ioni sono distribuiti uniformemente, senza riguardo per le loro interazioni elettrostatiche.[3]p. 227

La densità di carica è in relazione al numero di densità:[3]p. 233

${\displaystyle \rho =\sum _{i}z_{i}qn_{i}=\sum _{i}z_{i}qn_{i}^{0}e^{-{\frac {z_{i}q\varphi }{k_{B}T}}}.}$

Quando si combina questo risultato per la densità di carica con l'equazione di Poisson dall'elettrostatica, si ottiene la seguente equazione[3]p. 233:

Equazione di Poisson–Boltzmann

${\displaystyle \nabla ^{2}\varphi =-{\frac {\rho }{\varepsilon _{r}\varepsilon _{0}}}=-\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}e^{-{\frac {z_{i}q\varphi }{k_{B}T}}}.}$

Questa equazione è difficile da risolvere e non segue il principio di sovrapposizione per la relazione tra il numero di cariche e l'intensità del campo potenziale. È stata risolta dal matematico svedese Thomas Hakon Grönwall e dai suoi collaboratori V. K. La Mer (chimico) e Karl Sandved (fisico) in un articolo del 1928 redatto dalla rivista Physikalische Zeitschrift che trattava le estensioni alla teoria di Debye-Huckel, e ricorreva all'espansione in serie di Taylor.

Tuttavia, per concentrazioni di ioni sufficientemente basse, si può usare un'approssimazione al primo ordine dell'espansione in serie di Taylor per la funzione esponenziale (${\displaystyle e^{x}\approx 1+x}$ per ${\displaystyle 0<x\ll 1}$) creando un'equazione differenziale lineare[1]section 2.4.2. D&H affermano che questa approssimazione vale a grandi distanze tra gli ioni,[3]p. 227 che equivale a dire che la concentrazione è bassa. Infine, affermano senza provarlo che l'aggiunta di più termini nell'espansione ha scarso effetto sulla soluzione finale.[3]p. 227 Dunque

${\displaystyle -\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}e^{-{\frac {z_{i}q\varphi }{k_{B}T}}}\approx -\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}\left(1-{\frac {z_{i}q\varphi }{k_{B}T}}\right)=-\left(\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}-\sum _{i}{\frac {z_{i}^{2}q^{2}n_{i}^{0}\varphi }{\varepsilon _{r}\varepsilon _{0}k_{B}T}}\right).}$

L'equazione di Poisson–Boltzmann si trasforma in[3]p. 233

${\displaystyle \nabla ^{2}\varphi =\sum _{i}{\frac {z_{i}^{2}q^{2}n_{i}^{0}\varphi }{\varepsilon _{r}\varepsilon _{0}k_{B}T}},}$

perché la prima sommatoria è nulla a causa della condizione di elettroneutralità.[3]p. 234

Nel calcolare il potenziale scalare si assegna alla parte costante della sommatoria un simbolo, diciamolo ${\displaystyle \kappa ^{2}}$. Inoltre, denotiamo con ${\displaystyle I}$ la forza ionica della soluzione. Abbiamo le relazioni:[3]p. 234

${\displaystyle \kappa ^{2}=\sum _{i}{\frac {z_{i}^{2}q^{2}n_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}k_{B}T}}={\frac {2Iq^{2}}{\varepsilon _{r}\varepsilon _{0}k_{B}T}},}$

${\displaystyle I={\frac {1}{2}}\sum _{i}z_{i}^{2}n_{i}^{0}.}$

Quindi, l'equazione fondamentale è ridotta alla:[7]

Equazione di Helmholtz

${\displaystyle \nabla ^{2}\varphi =\kappa ^{2}\varphi .}$

Attualmente, ${\displaystyle \kappa ^{-1}}$ viene detto lunghezza preferita di Debye. D&H riconobbero l'importanza di tale parametro nel loro articolo e lo caratterizzano come una misura dello spessore dell'atmosfera ionica, cioè un doppio strato elettrico del tipo Gouy–Chapman.[3]p. 229

L'equazione si può esplicitare in coordinate sferiche prendendo ${\displaystyle r=0}$ per uno ione arbitrario:[3][8]p. 229

${\displaystyle \nabla ^{2}\varphi ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \varphi (r)}{\partial r}}\right)={\frac {\partial ^{2}\varphi (r)}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial \varphi (r)}{\partial r}}=\kappa ^{2}\varphi (r).}$

Tale equazione ha soluzione generale (notare che ${\displaystyle \kappa }$ è una costante positiva):[3]p. 229

${\displaystyle \varphi (r)=A{\frac {e^{-{\sqrt {\kappa ^{2}}}r}}{r}}+A'{\frac {e^{{\sqrt {\kappa ^{2}}}r}}{2r{\sqrt {\kappa ^{2}}}}}=A{\frac {e^{-\kappa r}}{r}}+A''{\frac {e^{\kappa r}}{r}}=A{\frac {e^{-\kappa r}}{r}},}$

dove

${\displaystyle A}$, ${\displaystyle A'}$, ${\displaystyle A''}$ sono costanti indeterminate

Il potenziale elettrico è zero all'infinito per definizione, tale condizione implica ${\displaystyle A''=0}$.[3]p. 229

Nella fase successiva, D&H fecero l'ipotesi che vi sia un certo raggio ${\displaystyle a_{i}}$, oltre il quale nessuno ione nell'atmosfera può avvicinarsi al centro dello ione (carica). Questo raggio può essere dovuto alle dimensioni fisiche dello ione stesso, alle dimensioni degli ioni nella nuvola ionica e a tutte le molecole d'acqua che circondano gli ioni. Matematicamente, trattarono lo ione al centro come una carica puntuale a cui non ci si può avvicinare al di fuori del raggio ${\displaystyle a_{i}}$[3]p. 231.

Il potenziale di una carica puntiforme di per sé ha l'espressione

${\displaystyle \varphi _{\text{pc}}(r)={\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{r}}.}$

D&H affermarono che il potenziale totale all'interno della sfera è[3]p. 232

${\displaystyle \varphi _{\text{sp}}(r)=\varphi _{\text{pc}}(r)+B_{i}={\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{r}}+B_{i},}$

dove

${\displaystyle B_{i}}$ è una costante che rappresenta il potenziale aggiunto dall'atmosfera ionica

Non forniscono alcuna giustificazione del fatto che ${\displaystyle B_{i}}$ sia una costante. Tuttavia, si può notare che dev'essere così considerando che qualsiasi distribuzione di carica statica sferica è soggetta al teorema del guscio sferico. Tale teorema afferma che nessuna forza viene esercitata sulle particelle cariche all'interno di una sfera (di carica arbitraria)[9]. Poiché si presume che l'atmosfera ionica sia sfericamente simmetrica (in media temporale), con carica variabile in funzione del raggio ${\displaystyle r}$, allora si rappresenta come una serie infinita di gusci di carica concentrici. Pertanto, all'interno del raggio ${\displaystyle a_{i}}$, l'atmosfera ionica non esercita alcuna forza. Se la forza è zero, allora si deduce per definizione che il potenziale è una costante.

Combinando il modello a distribuzione continua che ha fornito l'equazione di Poisson-Boltzmann e il modello della carica puntiforme, nell'ipotesi che nel raggio ${\displaystyle a_{i}}$ vi sia la continuità di ${\displaystyle \varphi (r)}$ ed esista la sua derivata prima, otteniamo[3]p. 232

${\displaystyle \varphi (a_{i})=A_{i}{\frac {e^{-\kappa a_{i}}}{a_{i}}}={\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{a_{i}}}+B_{i}=\varphi _{\text{sp}}(a_{i}),}$

${\displaystyle \varphi '(a_{i})=-{\frac {A_{i}e^{-\kappa a_{i}}(1+\kappa a_{i})}{a_{i}^{2}}}=-{\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{a_{i}^{2}}}=\varphi _{\text{sp}}'(a_{i}),}$

${\displaystyle A_{i}={\frac {z_{i}q}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {e^{\kappa a_{i}}}{1+\kappa a_{i}}},}$

${\displaystyle B_{i}=-{\frac {z_{i}q\kappa }{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {1}{1+\kappa a_{i}}}.}$

Dalla definizione di energia potenziale elettrica, l'energia potenziale associata allo ione centrale nell'atmosfera ionica è[3]p. 230 & p. 232

${\displaystyle u_{i}=z_{i}qB_{i}=-{\frac {z_{i}^{2}q^{2}\kappa }{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {1}{1+\kappa a_{i}}}.}$

Si noti che ciò richiede solo la conoscenza della carica dello ione centrale della nuvola e del potenziale di tutti gli altri ioni.

Per calcolare l'energia potenziale dell'intera soluzione elettrolitica, è necessario utilizzare la generalizzazione a carica multipla per l'energia potenziale elettrica:[3]p. 230 & p. 232

${\displaystyle U_{e}={\frac {1}{2}}\sum _{i=1}^{s}N_{i}u_{i}=-\sum _{i=1}^{s}{\frac {N_{i}z_{i}^{2}}{2}}{\frac {q^{2}\kappa }{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {1}{1+\kappa a_{i}}}.}$

Equazione di Debye–Hückel estesa

Sono stati proposti numerosi approcci per estendere la validità della legge agli intervalli di concentrazione che comunemente s'incontrano in chimica.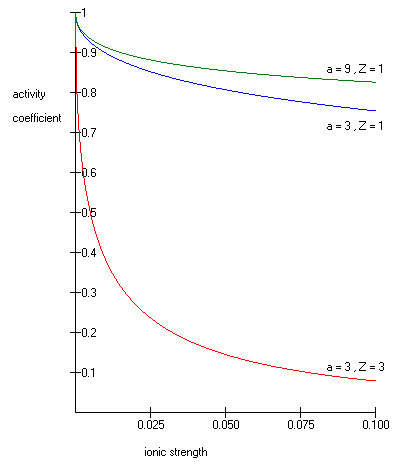

Grafico dell'equazione D&H estesa con valori differenti del numero di carica ionica ${\displaystyle Z=|z_{+}z_{-}|}$ e del diametro ionico ${\displaystyle a}$

Quindi la legge limite di Debye-Huckel avendo una gamma limitata applicativa allora i chimici hanno aggiunto un termine per tenere conto del fatto che lo ione centrale ha un raggio finito. Così l'equazione di D&H estesa ha un termine detto diametro ionico (${\displaystyle a}$). Questo termine tiene conto del fatto che gli ioni hanno un raggio finito e non sono cariche puntiformi. Il parametro della dimensione dello ione non ha un chiaro significato fisico. È troppo grande per corrispondere al raggio ionico di uno ione. Pertanto deve includere il concetto di raggio idratato. Il raggio idratato effettivo dello ione, è il raggio dello ione e delle molecole di acqua strettamente legate ad esso. Ioni grandi e ioni meno carichi legano l'acqua meno strettamente e hanno raggi idratati più piccoli degli ioni più piccoli e più caricati. Valori tipici sono 3Å per ioni come H^+,Cl^−, CN^−, e HCOO^−. Mentre il diametro effettivo dello ione idronio è 9Å[10]. In realtà è semplicemente un parametro regolabile che è stato utilizzato dai ricercatori per estendere empiricamente e adattare l'equazione a una maggiore forza ionica.

L'equazione comunemente utilizzata per il coefficiente di attività di uno ione singolo in una soluzione di uno o più elettroliti che fornisce risultati accurati per ${\displaystyle I\leq 0.1M}$ è data da:

${\displaystyle \ln(\gamma _{i})=-{\frac {A{z_{i}}^{2}{\sqrt {I}}}{1+Ba{\sqrt {I}}}}\,}$

${\displaystyle \log _{10}(\gamma _{i})=-{\frac {A}{\ln 10}}\,{\frac {{z_{i}}^{2}{\sqrt {I}}}{1+Ba{\sqrt {I}}}}\,}$

Mentre il coefficiente di attività ionico medio per una soluzione con un singolo elettrolita, tenendo conto della sua definizione, della condizione di elettroneutralità e dalle relazioni precedenti, ha l'espressione:

${\displaystyle \ \ln(\gamma _{\pm })=-{\frac {A|z_{+}z_{-}|{\sqrt {I}}}{1+Ba{\sqrt {I}}}}\,}$

${\displaystyle \ \log _{10}(\gamma _{\pm })=-{\frac {A}{\ln 10}}{\frac {|z_{+}z_{-}|{\sqrt {I}}}{1+Ba{\sqrt {I}}}}\,}$

dove

Simbolo	Definizione
${\displaystyle \ \gamma _{\pm }\,}$	Il coefficiente di attività ionico medio
${\displaystyle \ z_{+}\,z_{-}\,}$	I numeri di carica del catione e l'anione del soluto (ad esempio in HCl: ${\displaystyle z_{+}=1}$ per H^+,${\displaystyle z_{-}=-1}$ per Cl^-).)
${\displaystyle \ I\,}$	La forza ionica della soluzione acquosa espressa in molalità
${\displaystyle \ a\,}$	Il diametro effettivo dello ione in Ångström
${\displaystyle \ A\,}$ ${\displaystyle \ B\,}$	Le costanti con valori, nell'ordine, 1.172 (equazione con ${\displaystyle \ln }$, 0.509 se usiamo il ${\displaystyle \log _{10}}$) e 0.3281 per acqua a 25 °C

Poiché il lato destro dell'equazione è negativo a molalità di soluto finite e diventa nullo a diluizione infinita, la teoria prevede che ${\displaystyle \gamma _{\pm }}$ sia inferiore a 1 a molalità di soluto finite e si avvicina a 1 a diluizione infinita, come si nota dal grafico a sinistra dell'equazione.

Per soluzioni ad elevata forza ionica, in particolare fino a ${\displaystyle I<0.5M}$, dove M indica la molarità, è preferibile l’utilizzo di un’altra equazione, che in realtà deriva da quelle già viste, nota come equazione di Davies. Per valori maggiori, si dovrebbero usare le equazioni di Pitzer. In queste soluzioni il coefficiente di attività aumenta sensibilmente con la forza ionica.

L'equazione di Debye–Hückel non può essere utilizzata nelle soluzioni di tensioattivi dove la presenza di micelle influenzano le proprietà elettrochimiche del sistema (il calcolo sovrastima approssimativamente ${\displaystyle \gamma }$ per circa il 50%).

Verifiche sperimentali delle equazioni di Debye–Hückel

Per verificare la validità delle equazioni di Debye–Hückel sono state seguite molte vie sperimentali per la misura dei coefficienti di attività: il problema è che dobbiamo andare verso diluizioni molto elevate. Esempi tipici sono: misure di tensione di vapore, punto di congelamento, pressione osmotica (metodo indiretto) e misura del potenziale elettrico in pile (metodo diretto).

Andando verso diluizioni elevate sono stati trovati buoni risultati utilizzando cellule a membrana liquide, è stato possibile studiare soluti acquosi con concentrazione dell'ordine di ${\displaystyle 10^{-4}M}$ ed è stato trovato che

Grafici γ± di HCl in acqua calcolato e sperimentale.

1. Per 1:1 elettroliti (NaCl, KCl, HCl ...) l'equazione D&H è corretta.

   Come esempio prendiamo il coefficiente di attività ionico medio di HCl in acqua a 25 °C[11]. Nell'immagine a destra notiamo tre curve:

   • Continua: sperimentale
   • A tratti: Equazione D&H estesa (${\displaystyle a\,=\,5\cdot {10}^{-10}\,m}$, dove m sta per metri)
   • A punti: Equazione D&H limitata.

   La figura mostra che con l'opportuna scelta del parametro ${\displaystyle a}$, il coefficiente di attività ionica media di HCl calcolato (curva a punti) concorda strettamente con la sperimentale (curva continua) a basse molalità (diluizione infinita).

2. Per 2:2 (MgSO₄,...) o 3:2 (Al₂(SO₄)₃,...) elettroliti si trovano deviazioni negative dell'equazione D&H limitata: questo strano comportamento può essere osservato solo nella parte molto diluita, mentre nelle regioni più concentrate la deviazione diventa positiva.

È possibile che l'equazione di Debye–Hückel non sia in grado di prevedere questo comportamento a causa della linearizzazione dell'equazione di Poisson–Boltzmann, o forse non è questa la soluzione. Gli studi sono stati avviati solo negli ultimi anni del 20º secolo perché prima non era possibile indagare la regione ${\displaystyle 10^{-4}M}$, quindi è possibile che nei prossimi anni nascano nuove teorie.

Note

1. (EN) Hamann, Hamnett, e Vielstich, Electrochemistry, Weinheim, Wiley-VCH Verlag GmbH, 1988, ISBN 3-527-29096-6.
2. (EN) John B. Hudson, Electrolyte solutions - The Debye–Hückel theory (PDF), su Rensselaer Polytechnic Institute (RPI). URL consultato il 7-2-2022.
3. (EN) Peter J. W. Debye, The Collected Papers of Peter J. W. Debye, NY, Interscience Publishers, Inc., 1954.
4. (EN) Michael J. Braus, Debye, P. & Hückel, E. (1923) The theory of electrolytes. I. Freezing point depression and related phenomenon (Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen), su MINDS@UW, 2029. URL consultato il 7-2-2022.
5. (EN) William R. Salzman, Mixtures; Partial Molar Quantities; Ideal Solutions, su chem.arizona.edu, University of Arizona, 21 agosto 2001. URL consultato l'8 febbraio 2022 (archiviato dall'url originale il 7 giugno 2007).
6. (EN) section 19.3, su pma.caltech.edu. URL consultato il 7 febbraio 2022 (archiviato dall'url originale il 28 agosto 2007).
7. (EN) Deyu Lu, Like-charge attraction (PDF), su guava.physics.uiuc.edu, Department of physics University of Illinois at Urbana-Champaign, 7 maggio 2004. URL consultato il 7 febbraio 2022.
8. (EN) C.R. Nave, HyperPhysics: LaPlace's and Poisson's Equations, su hyperphysics.phy-astr.gsu.edu, Department of Physics and Astronomy (GSU), 2016. URL consultato il 7 febbraio 2022.
9. (EN) C.R. Nave, HyperPhysics: Potential and Charged Conducting Sphere, su hyperphysics.phy-astr.gsu.edu, Department of Physics and Astronomy (GSU), 2016. URL consultato il 7 febbraio 2022.
10. (EN) Douglas A. Skoog; D.M. West; F.J. Holler; S.R. Crouch, Fundamentals of Analytical Chemistry, 9ª ed., Cengage Learning, 2013, ISBN 9781285607191.
11. (EN) Herbert S. Harned; Benton B. Owen, 11 (tabella 5.1), in The Physical Chemistry of Electrolytic Solutions, American chemical society Monograph series, 137, 3ª ed., New York, Reinhold, 1958, ISBN 9780278917293.

Bibliografia

• (DE) P. Debye; E. Hückel, Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen (PDF), in Physikalische Zeitschrift, vol. 24, n. 9, 1923, pp. 185–206.
• (EN) Daniel C. Harris, Quantitative Chemical Analysis, 6ª ed., NY, W. H. Freeman and Company, 2013, ISBN 0-7167-4464-3.
• (EN) Activity and osmotic coefficients from the EMF of liquid membrane cells, VI - ZnSO4, MgSO4, CaSO4 and SrSO4 in water at 25 C.. F. Malatesta, R. Zamboni. J. Solution Chem.; 1997; 26() pp 791–815. DOI: 10.1007/BF02767784

Voci correlate

• Elettrolita forte
• Elettrolita debole
• Atmosfera ionica
• Teoria di Debye-Hückel
• Equazione di Poisson–Boltzmann

Collegamenti esterni

• (EN) Compendium of Chemical Terminology, 2ed, IUPAC, ("Gold Book") (1997). Versione online: (2006–) "Debye–Hückel equation".DOI: 10.1351/goldbook.D01534