|
Curva di Koch La curva di Koch, detta anche merletto di Koch[1], è una delle prime curve frattali di cui si conosca una descrizione. Apparve per la prima volta su un documento del 1904 del matematico svedese Helge von Koch[2]. La curva, infinitamente frastagliata, ha lunghezza infinita, ed è un esempio di curva continua e non derivabile. Generazione della curvaLa generazione della curva di Koch avviene grazie all'esecuzione ripetuta di un programma di istruzioni o procedura ricorsiva: è una procedura perché precisamente definita da un numero finito di passi, è ricorsiva perché viene ripetuta meccanicamente. L'algoritmo della curva consiste nella ripetizione del ciclo sottostante:
 Partendo da un segmento, se ne ottengono quindi quattro (costituenti una linea spezzata) nel primo ciclo, 4x4=16 nel secondo ciclo e così via, generando al limite un elegantissimo frattale. Ingrandendo un qualunque dettaglio del frattale si ottiene ancora lo stesso frattale: in questo consiste l'auto similarità e la struttura fine dei frattali a qualunque livello di scala.  Definizione matematicaIn ogni passo della generazione della curva che abbiamo descritto otteniamo una curva continua che possiamo pensare parametrizzata da una funzione continua sull'intervallo . Se si definiscono le parametrizzazioni in modo "ragionevole" si ha che la curva corrispondente ad ogni passo differisce dalla curva del passo precedente di quantità via via sempre più piccole. Si può dimostrare che questa successione di curve è una successione di Cauchy nello spazio di Banach delle curve continue su e quindi deve convergere ad un punto limite nello spazio delle curve continue, questo limite è la Curva di Koch. La curva di Koch così definita gode delle seguenti proprietà: 
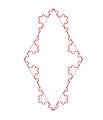
La curva di Koch e i matematiciNel suo libro Les objets fractals Benoît Mandelbrot propone la curva di Koch come un modello sommario della costa di un'isola. Essa è una celebre figura che Cesàro descrive nel seguente modo: «È questa similitudine tra il tutto e le sue parti, perfino quelle infinitesimali, che ci porta a considerare la curva di Koch alla stregua di una linea veramente meravigliosa tra tutte. Se fosse dotata di vita, non sarebbe possibile annientarla senza sopprimerla al primo colpo, poiché in caso contrario rinascerebbe incessantemente dalle profondità dei suoi triangoli, come la vita nell'universo». Lévy scrisse altresì: «Senza dubbio la nostra intuizione prevedeva che l'assenza di tangente e la lunghezza infinita della curva fossero legate a dei tornanti infinitamente piccoli che non si può pensare di disegnare. Ma si rimane confusi per il fatto che la nostra immaginazione non riesce nemmeno a spingersi oltre i primi passi nella costruzione di questi tornanti infinitamente piccoli». Sulla falsariga di Lévy, Stainhaus scrisse: «Ci avviciniamo alla realtà, considerando che la maggior parte degli archi che s'incontrano nella natura sono non rettificabili. Questa affermazione contrasta con la credenza che gli archi non rettificabili siano un'invenzione dei matematici, e che gli archi naturali siano rettificabili: si verifica invece il contrario». Charles Hermite, legato a una certa idea di purezza della funzione geometrica, davanti alla curva di Koch dichiarava di «ritrarsi con spavento e orrore da questa piaga lamentevole delle funzioni che non hanno derivata». Fiocco di neve di Koch  Questa curva è conosciuta anche col nome fiocco di neve di Koch (o stella/isola di Koch), anche se, in questo caso, oltre la curva si considera anche la superficie che essa racchiude. La costruzione parte da un'isola a forma di triangolo equilatero. Quindi, sul terzo centrale di ciascuno dei tre lati di lunghezza unitaria, si colloca un promontorio a forma di triangolo equilatero, dai lati uguali a . Si ottiene così un esagono regolare stellato, o stella di David, il cui perimetro ha lunghezza uguale a . Allo stesso modo si procede per ciascuno dei suoi dodici lati, e così di seguito. Particolarità di questa figura è che ha superficie finita. Per quanto riguarda il perimetro, affermare che sia di lunghezza infinita non corrisponde al vero. Per quanto il limite per infinite iterazioni tenda ad infinito, la misura non ha dimensione uguale a , ma uguale a , cosa che non permette di definire la sua misura come lunghezza vera e propria. Infatti se per l'-esima iterazione denotiamo con il numero totale di lati, la lunghezza di un lato, il perimetro, l'area, l'area del triangolo iniziale e supponiamo per brevità di scrittura Risulta allora da cui mentre per l'area risulta da cui Antifiocco di neve di Koch Per costruire un antifiocco si parte dal triangolo equilatero. Si merlettano i tre lati seguendo l'algoritmo di Koch, ma invece di merlettarli verso l'esterno ottenendo il fiocco di neve, si merlettano verso l'interno.[3] Il perimetro dell'antifiocco, come quello del fiocco è infinito ma l'area del triangolo iniziale risulta diminuita invece che aumentata di (cioè per ogni lato merlettato) infatti: da cui L'antifiocco di neve evidenzia una figura frattale ripetuta all'infinito con aree decrescenti in progressione geometrica di ragione . Questa figura ha la forma di un fiocco di neve allungato, corrispondente alla fusione di due fiocchi in uno solo, ed è detta per questo, siamese di Koch. A differenza del fiocco e del siamese, l'antifiocco è autosimile infatti se, mantenendo il centro, si accorciano i tre bracci a partire dai siamesi più grandi, si ottiene un antifiocco più piccolo con area ridotta a dell'originale. [1] Siamese e anti-siamese di Koch  Per ottenere il siamese di Koch, variante del fiocco di neve, si parte da due triangoli equilateri con un lato in comune che si elimina ottenendo un rombo. Si procede quindi alla merlettatura verso l'esterno dei quattro lati secondo l'algoritmo di Koch.
Il perimetro di questa figura, essendo composta di curve di Koch, è infinito. L'area è invece . Infatti all'area del rombo, che è pari a quella di due triangoli equilateri, si deve aggiungere, per ognuno dei quattro lati, l'area in eccedenza dovuta alla merlettatura che, come si è visto precedentemente, è per ogni lato.  TassellazioniPupazzo di neve di KochPer ottenere il pupazzo di neve di Koch si parte da un rombo con angolo acuto di 60 gradi e ottuso di 120. Le metà adiacenti all'angolo acuto si merlettano esternamente mentre le altre internamente. La figura ottenuta al limite è il pupazzo di neve che ha la stessa area del rombo generante e di tutti i livelli successivi. Infatti le quattro merlettature esterne aggiungono la stessa area tolta dalle interne. Il pupazzo tassella il piano con figure identiche similmente a quanto fa il rombo. Il pupazzo di neve di Koch si può scomporre in tre fiocchi di neve, due piccoli e uno grande. Questo perché il rombo si può scomporre in un esagono regolare con due triangoli equilateri adiacenti a due lati opposti paralleli. Merlettando esternamente i triangoli, si ottengono i due fiocchi piccoli; merlettando internamente l'esagono, il fiocco grande.[1]
Tassellazione con pupazzi e fiocchi di KochSe in una tassellazione del piano con pupazzi di neve di Koch si sostituiscono le scomposizioni del pupazzo in fiocchi di neve, si ottengono tassellazioni con fiocchi di diverse taglie.
Tassellazioni con siamesi di KochSi può ottenere in molti modi, ma le taglie dei siamese sono infinite e decrescono in progressione geometrica.[1]
Note
Bibliografia
Altri progetti
Collegamenti esterni
Questi sono esempi di celebri costruzioni utilizzando il metodo Koch generalizzato:
|
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
















![{\displaystyle S_{n}=S_{n-1}+{\frac {\Delta }{3}}\left({\frac {4}{9}}\right)^{n-1}=\left[1+{\frac {1}{3}}\sum _{k=0}^{n-1}\left({\frac {4}{9}}\right)^{k}\right]\Delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c33db525b4d151d3f9471c65fa94c357b5d1451)




![{\displaystyle S_{n}=S_{n-1}-{\frac {\Delta }{3}}\left({\frac {4}{9}}\right)^{n-1}=\left[1-{\frac {1}{3}}\sum _{k=0}^{n-1}\left({\frac {4}{9}}\right)^{k}\right]\Delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad30e18d30545e6d03e7177be624771cc933fe67)