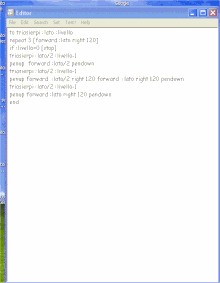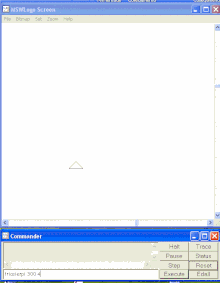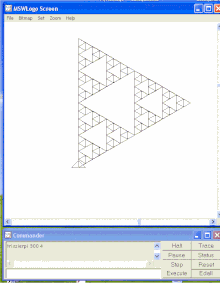
Triangolo di Sierpiński

Triangolo di Sierpiński

Il triangolo di Sierpiński è un frattale, così chiamato dal nome di Wacław Sierpiński che lo descrisse nel 1915. È un esempio base di insieme auto-similare, cioè matematicamente generato da un pattern che si ripete allo stesso modo su scale diverse. È una figura replicante di ordine tre potendosi scomporre in tre sue miniature.

Generazione attraverso limite di successioni

Si può ottenere il triangolo di Sierpiński dalle seguenti successioni infinite:

Partendo dal triangolo

IV livello del frattale in un mosaico cosmatesco del XIII secolo nel pavimento della Basilica di Santa Maria in Trastevere, Roma

• Livello 0 Si parte da un triangolo equilatero di lato a[1].
• Livello 1 Si congiungono i punti medi di ciascun lato individuando quattro triangoli simili al primo (di lato a/2) di cui tre ugualmente orientati e uno capovolto.
• Livello 2 Si ripete l'operazione di scomposizione precedente su ciascuno dei tre triangoli non capovolti ottenendo 9 triangolini non capovolti di lato a/4.
• Livello 3 Si ripete la stessa operazione sui 9 triangoli ottenendone 27 di lato a/8.
• Livello 4 Si ripete la stessa operazione sui 27 triangoli ottenendone 81 di lato a/16.
• .....
• Livello n Si ottengono ${\displaystyle 3^{n}}$ triangoli di lato ${\displaystyle 2^{-n}a}$ (ricordiamo che a è il lato del triangolo al livello 0).
• Continuando all'infinito il limite è il triangolo di Sierpiński.

• 
  I primi cinque livelli sopra descritti

Procedura in Logo

Animazione didattica per procedura in MSWLogo

Ecco la procedura ricorsiva per ottenere le varie fasi della costruzione. Questa è in funzione dei due parametri 'lato' e 'livello':

to triasierpi :lato :livello 
repeat 3 [forward :lato right 120]
if :livello=0 [stop]
triasierpi :lato/2 :livello-1
penup  forward :lato/2 pendown
triasierpi :lato/2 :livello-1
penup forward  :lato/2 right 120 forward  :lato right 120 pendown
triasierpi :lato/2 :livello-1
penup forward :lato right 120 pendown
end

La procedura scritta per MSWLogo[2][3], un linguaggio Logo per Windows, scaricabile gratuitamente dal sito della Softronics[4]. Dopo aver copiato e incollato la precedente procedura sull'Editor, la si può collaudare scrivendo, se si è scelto il lato di 300 pixel e il livello 4, nella linea dei comandi[5]:

triasierpi 300 4

Partendo dal quadrato

Osservando la successione precedente si nota che un triangolo nero viene sostituito da tre triangoli più piccoli disposti a triangolo. Si può fare anche con un quadrato.

• Livello 0 Si parte da un quadrato lato a.
• Livello 1 Si sostituisce il quadrato con 3 quadrati di lato a/2 disposti a triangolo: Due adiacenti e il terzo sopra.
• Livello 2 Si ripete l'operazione sostituendo i 3 quadrati ottenuti con analogo blocco di quadrati di lato dimezzato fino ad ottenere 9 quadrati di lato a/4.
• Livello 3 Si ripete l'operazione sostituendo i 9 quadrati ottenuti con analogo blocco di quadrati di lato dimezzato fino ad ottenere 27 quadrati di lato a/8.
• Livello 4 Si ripete l'operazione sostituendo i 27 quadrati ottenuti con analogo blocco di quadrati di lato dimezzato fino ad ottenere 81 quadrati di lato a/16.
• .....
• Livello n Si ripete l'operazione sostituendo i quadrati ottenuti con analogo blocco di quadrati di lato dimezzato fino ad ottenere ${\displaystyle 3^{n}}$ quadrati di lato ${\displaystyle 2^{-n}a}$.
• Continuando all'infinito il limite è il triangolo di Sierpinski.

• 
  Il livello 1
• 
  Il livello 2
• 
  Il livello 3
• 
  Il livello 4

Procedura in Logo

Ecco la procedura ricorsiva per ottenere i vari livelli della costruzione con quadrati. La procedura quadrato con parametro lato fa il quadrato. Mentre transierpiq con i due parametri 'lato' e 'livello' realizza la costruzione:

to quadrato :lato
repeat 4 [forward :lato right 90]
end
to triasierpiq :lato :livello 
if :livello=0 [quadrato :lato stop]
triasierpiq  :lato/2 :livello-1
penup right 90 forward :lato/2 lt 90 pendown
triasierpiq  :lato/2 :livello-1
penup forward :lato/2 right 90 back :lato/4 left 90 pendown
triasierpiq  :lato/2 :livello-1
penup right 90 back :lato/4 left 90 back :lato/2 pendown
end

Le procedure scritte per MSWLogo[2][3], un linguaggio Logo per Windows, scaricabile gratuitamente dal sito della Softronics[4]:, Dopo aver copiato e incollato le precedenti procedure sull'Editor, le si può collaudare immettendo, se si è scelto il lato di 256 pixel e il livello 6, nella linea dei comandi[5]:

triasierpiq 256 6

Partendo da un cagnolino

Quello che abbiamo visto precedentemente per triangoli equilateri e quadrati può essere esteso ad una immagine qualsiasi

• 

Curva di Sierpiński

• Livello 0 Si parte dalla metà di un esagono (semi-esagono) di lato a.
• Livello 1 Si sostituisce il secondo lato del semi-esagono con un semi-esagono di lato a/2 rivolto verso l'esterno. Si sostituiscono gli altri due lati con analoghi semiesagoni rivolti verso l'interno (dell'esagono a cui il semiesagono appartiene) ottenendo 3 semi-esagoni di lato a/2.
• Livello 2 Si ripete l'operazione di scomposizione precedente su ciascuno dei tre semi-esagoni ottenuti ottenendo 9 semi-esagoni di lato a/4.
• Livello 3 Si ripete l'operazione di scomposizione precedente su ciascuno dei 9 semi-esagoni ottenuti ottenendo 27 semi-esagoni di lato a/8.
• Livello 4 Si ripete l'operazione di scomposizione precedente su ciascuno dei 27 semi-esagoni ottenuti ottenendo 81 semi-esagoni di lato a/16.
• .....
• Livello n Si ottengono ${\displaystyle 3^{n}}$ semi-esagoni di lato ${\displaystyle 2^{-n}a}$.
• Continuando all'infinito il limite è il triangolo di Sierpiński.

• 
  Il livello 0
• 
  Il livello 1
• 
  Il livello 2
• 
  Il livello 5

Procedura in Logo

Ecco la procedura ricorsiva per ottenere i vari livelli della curva di Sierpiński nelle varie fasi della costruzione. Questa è in funzione dei due parametri 'lato' e 'livello':

to triasierpic :lato :livello 
if :livello=0 [repeat 3 [forward :lato right 60]
penup repeat 3 [forward :lato right 60] pendown stop]
penup  fd :lato pendown right 60
right 60 triasierpic :lato/2 :livello-1 left 60
left 60 triasierpic :lato/2 :livello-1 right 60
penup  fd :lato pendown right 60
penup fd :lato  pendown
right 120 triasierpic :lato/2 :livello-1 
penup forward :lato*2 pendown rt 120
end

La procedura scritta per MSWLogo[2][3], un linguaggio Logo per Windows, scaricabile gratuitamente dal sito della Softronics[4]. Dopo aver copiato e incollato la precedente procedura sull'Editor, la si può collaudare immettendo, se si è scelto il lato di 160 pixel e il livello 6, nella linea dei comandi[5]:

triasierpic 160 5

Sequenza di crescita a "pianta grassa"

Ecco un modo alternativo di costruzione partendo ancora dal triangolo equilatero.

• Livello 0 Si parte da un equilatero di lato a.
• Livello 1 Dal punto medio di ciascun lato "germoglia" un nuovo equilatero con lato a/2 con altezza perpendicolare al lato.
• Livello 2 Dal punto medio di ciascuno dei lati dei 3 triangoli precedenti "germogliano" in totale 9 triangoli di lato a/4.
• Livello 3 Dal punto medio di ciascuno dei lati dei 9 triangoli precedenti "germogliano" in totale 27 triangoli di lato a/8.
• Livello 4 Dal punto medio di ciascuno dei lati dei 27 triangoli precedenti "germogliano" in totale 81 triangoli di lato a/16.
• .....
• Livello n Dal punto medio di ciascuno dei lati dei ${\displaystyle 3^{n-1}}$ triangoli precedenti "germogliano" in totale ${\displaystyle 3^{n}}$triangoli di lato ${\displaystyle 2^{-n}a}$.
• Continuando all'infinito il limite è il triangolo di Sierpiński.

• 
  Il livello 1
• 
  Il livello 2
• 
  Il livello 3
• 
  Il livello 4

Procedura in Logo

Ecco la procedura ricorsiva per ottenere i vari livelli della costruzione per successive crescite esterne. La procedura equilatero con parametro lato fa il triangolo equilatero con la punta in basso. Mentre triansierpiequi con i due parametri 'lato' e 'livello' realizza la costruzione:

to equilatero :lato
left 30
repeat 3 [forward :lato right 120]
right 30 
end
to triasierpiequi :lato :livello 
equilatero :lato 
if :livello=0 [stop]
penup right 30 forward :lato/2 pendown
right 90 
triasierpiequi :lato/2 :livello-1 
left 90
penup forward -:lato/2 left 30 pendown
penup left 30 forward :lato/2 pendown
left 90 
triasierpiequi :lato/2 :livello-1 
right 90
penup forward -:lato/2 right 30 pendown
penup forward :lato/2*sqrt 3 pendown
triasierpiequi  :lato/2 :livello-1
penup forward -:lato/2*sqrt 3 pendown
 end

Le procedure scritte per MSWLogo[2][3], un linguaggio Logo per Windows, scaricabile gratuitamente dal sito della Softronics[4]:, Dopo aver copiato e incollato le precedenti procedure sull'Editor, le si può collaudare immettendo, se si è scelto il lato di 200 pixel e il livello 3, nella linea dei comandi[5]:

triasierpiequi 200 3

Proprietà

Successione ricorsiva con cerchi (neri per i dispari) al posto dei quadrati e triangolo di Tartaglia

Dimensione frattale

• Il triangolo di Sierpiński ha dimensione di Hausdorff log(3)/log(2) ≈ 1,585 e l'area del triangolo di Sierpiński è zero (in misura di Lebesgue)[6].

Triangolo di Tartaglia in modulo 2

Il triangolo di Tartaglia in modulo due all'aumentare delle righe tende al triangolo di Sierpinski[7]. Si ricorda che i numeri interi, presi in modulo 2, se sono dispari danno 1, se invece sono pari danno zero. Si possono fare facili verifiche considerando la successione di quadrati vista sopra. Prendendo ad esempio il livello 3 troviamo otto file di quadrati tra bianchi e colorati. La fila superiore ha un quadrato, poi 2, 3 , 4 ... fino a quella inferiore con ${\displaystyle 2^{3}}$ quadrati per un totale numero triangolare di 36 quadrati. A questo punto basta sovrapporre ai quadrati le prime 8 righe del triangolo di Tartaglia per constatare che i numeri dispari corrispondono ai quadrati colorati, mentre i pari a quelli bianchi. Ad esempio, l'ultima riga fatta di tutti triangoli colorati corrisponde ai coefficienti binomiali del binomio elevato alla settima potenza che sono tutti dispari[8]. Vedi figura per livello 5.

Curiosità

Una costruzione modulare

Marco Monti, ingegnere meccanico, insegnante e autore di alcune fiabe sui frattali[9], con 6561 moduli di legno appositamente ideati, con la collaborazione degli alunni, costruisce grandi triangoli di Sierpiński a scopo educativo[10]

Note

1. La procedura è in realtà estendibile a triangoli qualsiasi, vedi per esempio aurei acutangoli, su Maecla,Tartapelago, 2005. URL consultato il 25 dicembre 2018.
2. accesso a MSWLogo dal Tartapelago, su Maecla,Tartapelago, 2005. URL consultato il 25 dicembre 2018.
3. Piccolo vocabolario animato. Primitive scelte della geometria della tartaruga dell'MSWLogo, su Maecla,Tartapelago, 2005. URL consultato il 27 dicembre 2018.
4. Welcome to Softronics, Inc. An Educational Software Company, su Softronix. URL consultato il 25 dicembre 2018.
5. vedi immagini didattiche in: Sierpinski con MSWLogo, su commons.wikimedia.org.
6. Dimensione frattale, su tomma25.altervista.org. URL consultato il 27 dicembre 2018.
7. Elisa Agostini, dm.unife.it, http://dm.unife.it/divulgazione/2015/doc/a_tartaglia1.pdf Titolo mancante per url url (aiuto).
8. Successione quadrati al livello 3 corrispondente ai dispari (1 modulo 2) del triangolo di Tartaglia, in giallo (GIF), su commons.wikimedia.org.
9. Marco Monti, Numeri in rivolta, Illustrazioni di Silvia Peruzzi, Haiku, 2018, p. quarta di copertina, ISBN 978-88-98149-41-4.
10. Marta Cenu, Word fetcher, su wordfetcher.com.

Voci correlate

• Curva di Sierpiński
• Triangolo di Tartaglia
• Lista di frattali per dimensione di Hausdorff
• MSWLogo

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sul triangolo di Sierpiński

Collegamenti esterni

• (EN) Sierpiński gasket, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Triangolo di Sierpiński, su MathWorld, Wolfram Research.
• Giorgio Pietrocola, Vortice di triangoli di Sierpinski, su Tartapelago, Maecla, 2007. URL consultato il 25 dicembre 2018.
• Giorgio Pietrocola, Testuggine marina trigonoforme, su Tartapelago, Maecla, 2005. URL consultato il 25 dicembre 2018.
• Conversano, Tedeschini Lalli, Sierpiński Triangles in Stone, on Medieval Floors in Rome, 2011

Controllo di autorità	GND (DE) 4267564-9