Solide de Platon

En géométrie euclidienne,  un solide de Platon est l’un des cinq polyèdres à la fois réguliers et convexes.

En référence au nombre de faces (4, 6, 8, 12 et 20) qui les composent, ils sont nommés couramment tétraèdre (régulier), hexaèdre (régulier) ou cube, octaèdre (régulier), dodécaèdre (régulier) et icosaèdre (régulier), les adjectifs « régulier » et « convexe » étant souvent implicites ou omis quand le contexte le permet[1].

Les cinq polyèdres réguliers convexes (solides de Platon)
Tétraèdre	Cube	Octaèdre	Dodécaèdre	Icosaèdre
4 faces	6 faces	8 faces	12 faces	20 faces

Dans ce portrait, par Jacopo de' Barbari, de Luca Pacioli, auteur de De divina proportione, un dodécaèdre régulier est représenté en bas à droite.

Depuis les mathématiques grecques, les solides de Platon furent un sujet d’étude des géomètres en raison de leur esthétique et de leurs symétries. Leur nom, donné en l’honneur du philosophe grec Platon, rappelle une de ses théories, associant quatre d’entre eux aux quatre éléments de l’ancienne physique et le cinquième à la quintessence ou Éther.

Histoire

Selon une étude, les peuples néolithiques d'Écosse auraient construit des modèles en pierre des « cinq solides » au moins 1 000 ans avant Platon (Atiyah et Sutcliffe 2003). Ces modèles sont gardés au Ashmolean Museum à Oxford. Mais cette conclusion est hâtive[2].

Dans l'histoire des mathématiques de la Grèce antique, on peut tracer la chronologie suivante. Les pythagoriciens ont eu une connaissance empirique de trois solides : le tétraèdre (la pyramide), l'hexaèdre (le cube), le dodécaèdre (douze faces). Selon Proclos, Pythagore lui-même (vers 530 av. J.-C.) aurait eu connaissance de ces solides. Mais ce peut être son disciple Hippase de Métaponte (qui aurait construit le premier dodécaèdre) ou, plus vraisemblablement, Archytas de Tarente (vers 360 av. J.-C.).^[réf. nécessaire]

Il n'est pas fait mention de la pyramide avant Démocrite (fragment 155), actif vers 430 av. J.-C. Archytas aurait le premier construit le cube, pour résoudre le problème de la duplication du carré. Le premier, Platon mentionne le dodécaèdre, dans le Phédon (110 b), qui date d'env. 383 av. J.-C. Le mathématicien Théétète d'Athènes (mort en 395 ou 360 av. J.-C.) a découvert les deux autres solides : l'octaèdre et l'icosaèdre ; surtout, il les a construits, le premier, tous les cinq[3].

Les solides de Platon jouent un rôle déterminant dans la philosophie de Platon, à partir duquel ils ont été nommés. Platon, dans le dialogue Timée (env. 358 av. J.-C.), associait chacun des quatre éléments (la terre, l'air, l'eau et le feu) à un solide régulier.

• 
  Terre, dans Harmonice mundi de Kepler.
• 
  Eau, dans Harmonice mundi de Kepler.
• 
  Air, dans Harmonice mundi de Kepler.
• 
  Feu, dans Harmonice mundi de Kepler.
• 
  Éther, dans Harmonice mundi de Kepler.

La terre était associée au cube (Timée, 55 d), l'Air à l'octaèdre, l'Eau à l'icosaèdre et le Feu au tétraèdre. Il existait une justification pour ces associations : la chaleur du Feu semble pointue et comme un poignard (comme un peu le tétraèdre). L'Air est constitué de l'octaèdre ; ses composants minuscules sont si doux qu'on peut à peine les sentir. L'Eau, l'icosaèdre, s'échappe de la main lorsqu'on la saisit comme si elle était constituée de petites boules minuscules. Le solide le plus stable, l'hexaèdre (cube), représente la Terre. Ces petits solides font de la poussière lorsqu'ils sont émiettés et se cassent lorsqu'on s'en saisit, une grande différence avec l'écoulement doux de l'eau. Pour le cinquième solide, le dodécaèdre, Platon remarque obscurément : « le dieu l’a utilisé pour l'Univers quand il en a dessiné l’arrangement final. » Platon mettait en correspondance le dodécaèdre avec le Tout (Phédon, 110 b ; Timée, 55 c), parce que c'est le solide qui ressemble le plus à la sphère. Aristote a nommé ce cinquième élément, aithêr (aether en latin, « éther » en français) et a postulé que l'univers était fait de cet élément, et qu'il était substantiel à tous les autres, qu'il les contenait tous.

Modèle de Système solaire par des modèles de solides de Platon de Kepler issu du Mysterium Cosmographicum (1596).

Speusippe, le successeur de Platon à l'Académie (en 348 av. J.-C.) a repensé la tradition pythagoricienne sur les cinq solides (Pythagore, Hippase, Archytas).

Euclide a donné une description mathématique complète des solides de Platon dans les Éléments (env. 300 av. J.-C.) ; le dernier livre (livre XIII) est consacré à leurs propriétés. Les propositions 13–17 dans ce livre XIII décrit la construction du tétraèdre, de l'octaèdre, du cube, de l'icosaèdre et du dodécaèdre dans cet ordre. Pour chaque solide, Euclide trouve le rapport du diamètre à la sphère circonscrite à la longueur des arêtes. Dans la proposition 18, il argumente qu'il n'existe pas plus de polyèdres réguliers convexes. En effet, pour être régulier, un polyèdre doit posséder le même nombre de polygones réguliers en chacun de ses sommets et la somme des angles au sommet des polygones réguliers doit être strictement inférieure à 360° (voir démonstration[4]). Une grande partie des informations du livre XIII proviennent probablement du travail de Théétète.

Au XVI^e siècle, l'astronome allemand Johannes Kepler essaya de trouver une relation entre les cinq planètes connues à l'époque (en excluant la Terre) et les cinq solides de Platon. Dans le Mysterium Cosmographicum, publié en 1596, Kepler présenta un modèle de Système solaire dans lequel les cinq solides étaient fixés les uns dans les autres et séparés par une série de sphères inscrites et circonscrites. Les six sphères correspondaient chacune aux planètes (Mercure, Vénus, la Terre, Mars, Jupiter et Saturne). Les solides étaient ordonnés de l'intérieur vers l'extérieur, le premier étant l'octaèdre (Mercure), suivi de l'icosaèdre (Vénus), du dodécaèdre (Mars), du tétraèdre (Jupiter) et finalement le cube (Saturne). De cette manière, la structure du système solaire et les relations de distances entre les planètes étaient dictées par les solides de Platon. L'idée originale de Kepler dut être abandonnée, mais de cette recherche émergèrent la découverte des solides de Kepler, la constatation que les orbites des planètes ne sont pas des cercles, et les lois du mouvement planétaire de Kepler pour lesquelles il est maintenant célèbre.

Chaque solide de Platon répond à la formule d'Euler[4], démontrée en 1752 par le mathématicien suisse Leonhard Euler, obtenue avec un nombre F de faces, A d'arêtes et S de sommets : F + S – A = 2

Propriétés combinatoires

Un polyèdre convexe est un solide de Platon si et seulement si

1. Toutes ses faces sont des polygones réguliers convexes isométriques, c'est-à-dire superposables,
2. Aucune de ses faces ne se coupe, excepté sur les arêtes
3. Le même nombre de faces se rencontre à chacun de ses sommets.

Chaque solide de Platon peut par conséquent être noté par un symbole {p, q} où

p = le nombre de côtés de chaque face (ou le nombre de sommets sur chaque face) et

q = le nombre de faces se rencontrant à chaque sommet (ou le nombre d'arêtes se rencontrant à chaque sommet).

Le symbole {p, q}, appelé le symbole de Schläfli, donne une description combinatoire du polyèdre. Les symboles de Schläfli des cinq solides de Platon sont donnés dans la table ci-dessous.

Polyèdre		Sommets	Arêtes	Faces	Symbole de Schläfli	Configuration de sommet
Tétraèdre régulier		4	6	4 triangles équilatéraux	{3, 3}	3.3.3
Hexaèdre régulier (cube)		8	12	6 carrés	{4, 3}	4.4.4
Octaèdre régulier		6	12	8 triangles équilatéraux	{3, 4}	3.3.3.3
Dodécaèdre régulier		20	30	12 pentagones réguliers	{5, 3}	5.5.5
Icosaèdre régulier		12	30	20 triangles équilatéraux	{3, 5}	3.3.3.3.3

Toutes les autres informations combinatoires à propos de ces solides, telles que le nombre total de sommets (S), des arêtes (A) et des faces (F) peuvent être déterminées à partir de p et q. Puisque toute arête joint deux sommets et possède deux faces adjacentes, nous devons avoir :

${\displaystyle pF=2A=qS.\,}$

L'autre relation entre ces valeurs est donnée par la formule d'Euler :

${\displaystyle S-A+F=2.\,}$

Ce fait non-trivial peut être démontré d'une grande variété de manières (en topologie algébrique il découle de ce fait que la caractéristique d'Euler de la sphère est 2). Mises ensemble, ces trois relations déterminent complètement S, A et F :

${\displaystyle S={\frac {4p}{4-(p-2)(q-2)}},\quad A={\frac {2pq}{4-(p-2)(q-2)}},\quad F={\frac {4q}{4-(p-2)(q-2)}}.}$

Note : échanger p et q intervertit F et S laissant A inchangé (pour une interprétation géométrique de ce fait, voir la section sur les polyèdres duaux ci-dessous).

Classification

C'est un résultat classique qu'il existe seulement cinq polyèdres réguliers convexes. Deux arguments communs sont donnés ci-dessous. Les deux montrent seulement qu'il ne peut pas y avoir plus de cinq solides de Platon. Que chacun des cinq existe réellement est une question séparée — à laquelle on peut répondre par une construction explicite.

Démonstration géométrique

L'argument géométrique suivant est très similaire à celui donné par Euclide dans les Éléments :

1. Chaque sommet du solide doit coïncider avec un sommet sur au moins trois faces, sinon ce n'est qu'un point de côté et non un sommet.
2. À chaque sommet du solide, le total des angles entre les côtés adjacents relatifs aux faces adjacentes, doit être strictement inférieur à 360° (sinon, le solide ne peut pas être convexe).
3. Les angles de tous les sommets de toutes les faces d'un solide de Platon sont identiques, donc chaque sommet de chaque face doit contribuer pour strictement moins de 360°/3=120°.
4. Les polygones réguliers de six côtés ou plus ont seulement des angles de 120° ou plus, donc la face commune doit être le triangle, le carré ou le pentagone. Et pour :
   • les faces triangulaires : chaque sommet d'un triangle régulier a un angle de 60°, donc une forme doit avoir 3, 4 ou 5 triangles se rencontrant à un sommet ; celles-ci sont le tétraèdre, l'octaèdre et l'icosaèdre respectivement.
   • les faces carrées : chaque sommet d'un carré a un angle de 90°, donc il existe seulement un arrangement possible avec trois faces à un sommet, le cube.
   • les faces pentagonales : chaque sommet a un angle de 108° ; de nouveau, seulement un arrangement, de trois faces à un sommet est possible, le dodécaèdre.

Démonstration topologique

Une démonstration purement topologique peut être donnée en utilisant seulement les informations combinatoires sur les solides. La clé est l'observation d'Euler que ${\displaystyle S-A+F=2}$, et le fait que ${\displaystyle pF=2A=qS}$. En combinant ces équations, on obtient l'équation

${\displaystyle {\frac {2A}{q}}-A+{\frac {2A}{p}}=2.}$

En divisant par ${\displaystyle 2A}$ il vient

${\displaystyle {1 \over q}+{1 \over p}={1 \over 2}+{1 \over A}.}$

Puisque ${\displaystyle A}$ est strictement positif, nous devons avoir

${\displaystyle {\frac {1}{q}}+{\frac {1}{p}}>{\frac {1}{2}}.}$

En utilisant le fait que p et q doivent, tous deux, être au moins égaux à 3, on peut facilement voir qu'il existe seulement cinq possibilités pour {p, q} :

${\displaystyle \{3,3\},\quad \{4,3\},\quad \{3,4\},\quad \{5,3\},\quad \{3,5\}.}$

Propriétés géométriques

Angles

Il existe un nombre d'angles associés avec chaque solide de Platon. L'angle dièdre est l'angle interne entre deux faces planes quelconques. L'angle dièdre, θ, du solide {p, q} est donné par la formule

${\displaystyle \sin {\theta \over 2}={\frac {\cos(\pi /q)}{\sin(\pi /p)}}.}$

Ceci est quelquefois exprimé de manière plus pratique en termes de tangente par

${\displaystyle \tan {\theta \over 2}={\frac {\cos(\pi /q)}{\sin(\pi /h)}}.}$

La quantité h est 4, 6, 6, 10 et 10 pour le tétraèdre, le cube, l'octaèdre, le dodécaèdre et l'icosaèdre respectivement, autrement dit ${\displaystyle 4h=15+[2(p+q)-11]^{2}}$.

Le défaut angulaire (en) au sommet d'un polyèdre est la différence entre la somme des angles d'une face et 2π. Le défaut, δ, à un sommet quelconque des sommets de Platons {p, q} est

${\displaystyle \delta =2\pi -q\pi \left(1-{2 \over p}\right).}$

Par le théorème de Descartes, ceci est égal à 4π divisé par le nombre de sommets (i.e. le défaut total de tous les sommets est 4π).

L'analogue tridimensionnel d'un angle plan est un angle solide. L'angle solide, Ω, au sommet d'un solide de Platon est donné en termes d'angle dièdre par

${\displaystyle \Omega =q\theta -(q-2)\pi .\,}$

Ceci provient de la formule de l'excès sphérique pour un polygone sphérique et le fait que la figure de sommet du polyèdre {p, q} est un q-gone régulier.

Les divers angles associés avec les solides de Platon sont donnés ci-dessous. Les valeurs numériques des angles solides sont données en stéradians. La constante ${\displaystyle \varphi ={\frac {(1+{\sqrt {5}})}{2}}\,}$ est le nombre d'or.

Polyèdre	Angle dièdre ${\displaystyle (\theta )\,}$	${\displaystyle \tan {\frac {\theta }{2}}}$	défaut angulaire (en) ${\displaystyle (\delta )\,}$	Angle solide ${\displaystyle (\Omega )\,}$
Tétraèdre	70,53°	${\displaystyle 1 \over {\sqrt {2}}}$	${\displaystyle \pi \,}$	${\displaystyle 2\arctan \left({\frac {\sqrt {2}}{5}}\right)}$	${\displaystyle \approx 0,551286}$
Cube	90°	${\displaystyle 1\,}$	${\displaystyle \pi \over 2}$	${\displaystyle {\frac {\pi }{2}}}$	${\displaystyle \approx 1,57080}$
Octaèdre	109,47°	${\displaystyle {\sqrt {2}}}$	${\displaystyle {2\pi } \over 3}$	${\displaystyle 4\arcsin \left({1 \over 3}\right)}$	${\displaystyle \approx 1,35935}$
Dodécaèdre	116,56°	${\displaystyle \varphi \,}$	${\displaystyle \pi \over 5}$	${\displaystyle 2\arctan(\varphi ^{5})}$	${\displaystyle \approx 2,96174}$
Icosaèdre	138,19°	${\displaystyle \varphi ^{2}\,}$	${\displaystyle \pi \over 3}$	${\displaystyle 2\pi -5\arcsin \left({2 \over 3}\right)}$	${\displaystyle \approx 2,63455}$

Rayons, aires et volumes

Une autre vertu de la régularité est que les solides de Platon possèdent tous trois sphères concentriques :

• la sphère circonscrite qui passe à travers tous les sommets,
• la sphère médiane qui est tangente à chaque arête au milieu de celle-ci et
• la sphère inscrite qui est tangente à chaque face au centre de celle-ci.

Les rayons de ces sphères sont appelés les rayons circonscrits, les rayons moyens et les rayons internes. Ceux-ci sont les distances à partir du centre du polyèdre aux sommets, aux milieux des arêtes et aux centres de faces respectivement. Le rayon circonscrit R et le rayon interne r du solide {p, q} avec une longueur d'arête a sont donnés par

${\displaystyle R=\left({a \over 2}\right)\tan {\frac {\pi }{q}}\tan {\frac {\theta }{2}}}$

${\displaystyle r=\left({a \over 2}\right)\cot {\frac {\pi }{p}}\tan {\frac {\theta }{2}}}$

où θ est l'angle dièdre. Le rayon moyen ρ est donné par

${\displaystyle \rho =\left({a \over 2}\right){\frac {\cos(\pi /p)}{\sin(\pi /h)}}}$

où h est la quantité utilisée ci-dessus dans la définition de l'angle dièdre (h = 4, 6, 6, 10 ou 10). Noter que le rapport du rayon circonscrit au rayons interne est symétrique dans p et q :

${\displaystyle {R \over r}=\tan {\frac {\pi }{p}}\tan {\frac {\pi }{q}}.}$

La superficie A d'un solide de Platon {p, q} se calcule facilement ; elle est égale à l'aire d'un p-gone régulier multipliée par le nombre de faces F. C’est-à-dire :

${\displaystyle A=\left({a \over 2}\right)^{2}Fp\cot {\frac {\pi }{p}}.}$

Le volume est calculé comme étant F fois le volume de la pyramide dont la base est un p-gone régulier et dont la hauteur est le rayon interne r. C’est-à-dire :

${\displaystyle V={1 \over 3}rA.}$

Le tableau suivant liste les divers rayons des solides de Platon ainsi que leurs aires A et leurs volumes V, et deux taux de remplissage : les rapports entre ces volumes V et ceux, V_S = 4πR^3/3, de la sphère circonscrite et V_s = 4πr^3/3, de la sphère inscrite. La taille globale est fixée en prenant la longueur d'arête, a, égale à 2.

Polyèdre (a = 2)	r	ρ	R	A	V	V/VS[5]	Vs/V[6]
Tétraèdre	${\displaystyle 1 \over {\sqrt {6}}}$	${\displaystyle 1 \over {\sqrt {2}}}$	${\displaystyle {\sqrt {3 \over 2}}}$	${\displaystyle 4{\sqrt {3}}}$	${\displaystyle {\frac {2{\sqrt {2}}}{3}}}$	${\displaystyle {\frac {2}{3\pi {\sqrt {3}}}}\simeq 0{,}12}$	${\displaystyle {\frac {\pi }{6{\sqrt {3}}}}\simeq 0{,}30}$
Cube	${\displaystyle 1}$	${\displaystyle {\sqrt {2}}}$	${\displaystyle {\sqrt {3}}}$	${\displaystyle 24}$	${\displaystyle 8}$	${\displaystyle {\frac {2}{\pi {\sqrt {3}}}}\simeq 0{,}37}$	${\displaystyle {\frac {\pi }{6}}\simeq 0{,}52}$
Octaèdre	${\displaystyle {\sqrt {2 \over 3}}}$	${\displaystyle 1}$	${\displaystyle {\sqrt {2}}}$	${\displaystyle 8{\sqrt {3}}}$	${\displaystyle {\frac {8{\sqrt {2}}}{3}}}$	${\displaystyle {\frac {1}{\pi }}\simeq 0{,}32}$	${\displaystyle {\frac {\pi }{3{\sqrt {3}}}}\simeq 0{,}60}$
Dodécaèdre	${\displaystyle {\frac {\varphi ^{2}}{\xi }}}$	${\displaystyle \varphi ^{2}}$	${\displaystyle {\sqrt {3}}\,\varphi }$	${\displaystyle 60{\frac {\varphi }{\xi }}}$	${\displaystyle 20{\frac {\varphi ^{3}}{\xi ^{2}}}}$	${\displaystyle {\frac {\varphi }{\pi }}{\sqrt {5 \over 3}}\simeq 0{,}66}$	${\displaystyle {\frac {\pi \varphi ^{7/2}}{15{\sqrt[{4}]{5}}}}\simeq 0{,}75}$
Icosaèdre	${\displaystyle {\frac {\varphi ^{2}}{\sqrt {3}}}}$	${\displaystyle \varphi }$	${\displaystyle \xi \varphi }$	${\displaystyle 20{\sqrt {3}}}$	${\displaystyle {\frac {20\varphi ^{2}}{3}}}$	${\displaystyle {\frac {{\sqrt {\varphi }}{\sqrt[{4}]{5}}}{\pi }}\simeq 0{,}61}$	${\displaystyle {\frac {\pi \varphi ^{4}}{15{\sqrt {3}}}}\simeq 0{,}83}$

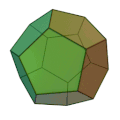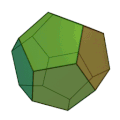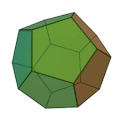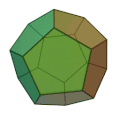
Les constantes φ et ξ ci-dessus sont données par

${\displaystyle \varphi =2\cos {\pi \over 5}={\frac {1+{\sqrt {5}}}{2}}\qquad \xi =2\sin {\pi \over 5}={\sqrt {\frac {5-{\sqrt {5}}}{2}}}=5^{1/4}\varphi ^{-1/2}.}$

Parmi les solides de Platon, le dodécaèdre ou l'icosaèdre peuvent être regardés comme la meilleure approximation de la sphère. L'icosaèdre a le plus grand nombre de faces, le plus grand angle dièdre, et son enveloppe est la plus proche de sa sphère inscrite. Le dodécaèdre, d'un autre côté, a le plus petit défaut angulaire, le plus grand angle solide au sommet et il remplit le plus sa sphère circonscrite.

Symétrie

Polyèdre dual

Image 1.   Les  douze  étoilements
des  faces  d’un  dodécaèdre  ont
les  douze  sommets  d’un
icosaèdre,   son  dual :
l’enveloppe  convexe  de
ses  deux  premiers  étoilements.

Image 2.   Le  solide  d'Archimède
qui  a  huit  faces  triangulaires  et  six  faces  carrées :
le  cuboctaèdre,   ou  vingt  faces  triangulaires
et  douze  pentagonales :  l’icosidodécaèdre,
est  ici  l’intersection  de  deux
polyèdres  duaux.

Image 3.   Autre  paire
de   polyèdres   duaux.

Image 4.   Possible construction
d’un octaèdre  de  Platon,
à  partir  de  son  dual.

Deux solides de Platon sont duaux l’un de l’autre quand l’un a autant de faces que l’autre a de sommets.  Ils ont alors autant d’arêtes l’un que l’autre,  d’après la formule d'Euler.

• Le tétraèdre régulier est son propre dual,  puisqu’il a quatre faces et quatre sommets :  autant de faces que de sommets.
• Le cube et l'octaèdre forment une paire duale.
• Le dodécaèdre et l'icosaèdre forment une autre paire duale.

Autrement dit,  le symbole de Schläfli  { p, q }  d’un polyèdre devient  { q, p }  chez son dual.

Les figures sont analogues dans les images 2 et 3 :  les arêtes d’une paire duale sont deux à deux perpendiculaires en leur milieu.  À droite,  les deux tétraèdres partagent trois sections carrées avec leur intersection :  un octaèdre de Platon.

En haut dans l’image 2,  on peut voir l’un ou l’autre solide d’Archimède construit en tronquant un solide de Platon.  Par exemple le cuboctaèdre est obtenu à partir de l’octaèdre,  en le tronquant à chaque sommet par un plan,  passant par les milieux des quatre arêtes issues de ce sommet.  L’octaèdre est ainsi privé à chaque sommet d’une pyramide régulière carrée.

Inversement,  en prolongeant les plans de toutes les faces semblables d’un cuboctaèdre ou d’un icosidodécaèdre,  on construit l’un des deux solides duaux,  qui correspondent au solide d’Archimède.  Par exemple,  prolonger les faces triangulaires revient à entourer de trois répliques chaque triangle dans son plan,  ou à l’agrandir à l’échelle 2 par une homothétie,  centrée au centre de la face équilatérale.  On obtient alors un octaèdre ou un icosidodécaèdre.  Ainsi chaque triangle de l’image 2,  tracé en noir,  est un agrandissement à l’échelle 2 du triangle concentrique au contour bigarré.  À droite,  on construit l’un ou l’autre des tétraèdres en prolongeant les plans d’une face sur deux de l’octaèdre,  ou en transformant une face sur deux de l’octaèdre par une homothétie de rapport ‑2,  analogue aux précédentes.  Autrement,  on prolonge les faces non triangulaires d’un cuboctaèdre ou d’un icosidodécaèdre par les plans des faces d’un cube ou d’un dodécaèdre.  Ces plans contiennent les faces des pyramides régulières triangulaires,  à ajouter au solide d’Archimède pour obtenir le cube ou le dodécaèdre.  Leurs arêtes sont épaisses dans l’image 2,  en kaki ou en rouge.  Il s’agit dans tous les cas d’étoiler partiellement,  à l’inverse de tronquer un polyèdre.

Deux arêtes des deux tétraèdres,  qui se coupent en leur milieu,  sont les diagonales perpendiculaires d’une face du cube de mêmes sommets que les tétraèdres :  les polyèdres réguliers ont les mêmes sommets dans les deux dernières figures,  des images 3 et 4.  En étoilant un octaèdre,  vous construisez les huit sommets d’un cube,  dual de l’octaèdre.  À l’inverse,  tronquez un cube par huit plans,  passant chacun par les trois sommets les plus proches du sommet tronqué,  et il vous reste un octaèdre.  D’une façon analogue,  l’enveloppe convexe d’un petit dodécaèdre étoilé est un dual du dodécaèdre de Platon :  un icosaèdre de Platon.

À droite dans l’image 4,  un dual de cube n’est donc plus construit en tronquant le cube comme précédemment,  et en prolongeant ensuite les faces triangulaires du cuboctaèdre obtenu.  Cette fois,  un sommet de l’octaèdre est placé au centre de chaque face du cube,  à l’intersection des diagonales du carré.  Cependant,  comme dans l’image 2,  les solides duaux sont concentriques,  et leurs arêtes deux à deux perpendiculaires.

Groupes de symétrie

En mathématiques, le concept de symétrie est étudié avec la notion de groupe mathématique. Chaque polyèdre possède un groupe de symétrie associé, qui est l'ensemble de toutes les transformations (isométries euclidiennes) qui laissent le polyèdre invariant. L'ordre du groupe de symétrie est le nombre de symétries du polyèdre. On fait souvent une distinction entre le groupe de symétrie total, qui inclut les réflexions, et le groupe de symétrie propre, qui inclut seulement les rotations.

Les groupes de symétrie des solides de Platon sont connus sous le nom de groupes polyédriques (en) (qui sont une classe particulière des groupes ponctuels en dimension trois (en)). Le haut degré de symétrie des solides de Platon peut être interprété de différentes manières. Pour la plus importante, les sommets de chaque sommet sont tous équivalents sous l'action du groupe de symétrie, comme sont les arêtes et les faces. On dit que l'action du groupe de symétrie est transitive sur les sommets, les arêtes et les faces. En fait, c'est une autre manière de définir la régularité d'un polyèdre : un polyèdre est régulier si et seulement s'il est de sommet uniforme, d'arête uniforme et de face uniforme.

Il existe seulement trois groupes de symétrie associés avec les solides de Platon plutôt que cinq, puisque le groupe de symétrie d'un polyèdre quelconque coïncide avec celui de son dual. Ceci est vu facilement en examinant la construction du polyèdre dual. Toute symétrie de l'original doit être une symétrie du dual et vice-versa. Les trois groupes polyédriques sont :

• le groupe tétraédrique T,
• le groupe octaédrique O (qui est aussi le groupe de symétrie du cube) et
• le groupe icosaédrique I (qui est aussi le groupe de symétrie du dodécaèdre).

Les ordres des groupes propres (rotations) sont 12, 24 et 60 respectivement — précisément, deux fois le nombre des arêtes dans le polyèdre respectif[7]. Les ordres des groupes de symétrie totaux sont deux fois de nouveau les ordres précédents (24, 48 et 120). En effet, l'action du groupe des rotations d'un solide de Platon sur ses arêtes est transitive (donc celle de son groupe de symétrie total aussi), et le nombre de rotations (resp. d'isométries) qui stabilisent une arête est égal à 2 (resp. 4).

Le tableau suivant liste les diverses propriétés de symétrie des solides de Platon. Les groupes de symétrie listés sont les groupes totaux avec les sous-groupes de rotation donnés entre parenthèses (comme pour le nombre de symétries). La construction kaléidoscopique de Wythoff est une méthode pour la construction des polyèdres directement à partir des groupes de symétrie. Nous listons la référence du symbole de Wythoff pour chaque solide de Platon.

Polyèdre	Symbole de Schläfli	Symbole de Wythoff	Polyèdre dual	Symétries	Groupe de symétrie
Tétraèdre	{3, 3}	3 | 2 3	Tétraèdre	24 (12)	Td (T)
Cube	{4, 3}	3 | 2 4	Octaèdre	48 (24)	Oh (O)
Octaèdre	{3, 4}	4 | 2 3	Cube
Dodécaèdre	{5, 3}	3 | 2 5	Icosaèdre	120 (60)	Ih (I)
Icosaèdre	{3, 5}	5 | 2 3	Dodécaèdre

En nature et en technologie

Dans la nature

Le tétraèdre, le cube et l'octaèdre apparaissent tous naturellement dans les structures cristallines. Ceux-ci n'épuisent nullement les nombres de formes possibles de cristaux. Néanmoins, ni l'icosaèdre régulier, ni le dodécaèdre régulier ne figurent parmi eux. Une de ces formes, appelée le pyritoèdre (nommé en rapport avec le groupe des minéraux avec lequel il est typique) a douze faces pentagonales, arrangées avec le même motif que les faces du dodécaèdre régulier. Néanmoins, les faces du pyritoèdre ne sont pas régulières, donc, le pyritoèdre n'est pas non plus régulier.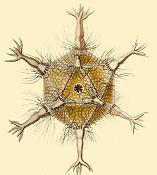

Circogonia icosahedra, une espèce de radiolaire, formée comme un icosaèdre régulier.

Au début du XX^e siècle, Ernst Haeckel décrivit[8] de nombreuses d'espèces de radiolaires, certaines comportant des squelettes ayant la forme de divers polyèdres réguliers. Ses exemples incluent Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus et Circorrhegma dodecahedra, les formes de ces créatures étant évidentes d'après leurs noms.

Beaucoup de virus, tel que le virus de l'herpès, ont la forme d'un icosaèdre régulier. Les structures virales sont construites sur des sous-unités de protéines identiques répétées et l'icosaèdre est la forme la plus facile à assembler en utilisant ces sous-unités. Un polyèdre régulier est utilisé car il peut être construit à partir d'une unité de protéine basique utilisée indéfiniment, ceci engendre un espace dans le génome viral.

Usage technologique

En météorologie et en climatologie, les modèles numériques globaux des flux atmosphériques sont d'un intérêt croissant. Ils emploient des grilles qui sont basées sur un icosaèdre (raffiné par triangulation) à la place de la grille longitude/latitude plus communément utilisée. Ceci a l'avantage d'avoir une résolution spatiale également distribuée sans singularités (i.e. les pôles géographiques) aux dépens d'une certaine difficulté numérique plus grande.

La géométrie des structures spatiales est souvent basée sur les solides de Platon. Dans le système MERO, les solides de Platon sont utilisés pour la convention de nomenclature des diverses configurations d'armatures d'espace. Par exemple ½O+T fait référence à une configuration faite d'un demi-octaèdre et un tétraèdre.

Dans les jeux de société

Par ailleurs, les solides de Platon sont souvent utilisés pour fabriquer des dés. Les dés à 6 faces sont très communs, mais les autres nombres sont communément utilisés dans les jeux de rôle. De tels dés sont souvent appelés dn où n est le nombre de faces (d8, d20, etc.).

Les dés polyédriques sont souvent utilisés dans les jeux de rôle sur table. On leur ajoute couramment le trapézoèdre pentagonal, qui n'est pas un solide de Platon.

Dans les années 1960, les joueurs de jeux de guerre ont éprouvé le besoin d'obtenir des valeurs aléatoires sur une plage plus importante que de 1 à 6 tout en gardant une fonction de densité uniforme (une « probabilité plate »), alors que si l'on ajoute plusieurs dés, on obtient une probabilité « en cloche », favorisant les résultats médian (conséquence théorème central limite). On évoquait déjà l'utilisation d'icosaèdres mais il était difficile de s'en procurer et ils étaient chers. En 1971, Gary Gygax utilise un système de jetons à piocher dans une boîte pour obtenir des résultats entre 1 et 20 pour le jeu Tractics (en)[9]. En découvrant du matériel pédagogique présentant des solides de Platon en plastique, Gary Gygax a l'idée de mettre des numéros dessus et les utilise pour Donjons et Dragons (1974)[10].

Ces formes apparaissent fréquemment dans d'autres jeux ou d'autres puzzles. Des puzzles similaires aux Rubik's Cube ont vu le jour dans toutes ces formes — voir Puzzle combinatoire (en).

Polyèdres reliés et polytopes

Polyèdres uniformes

Il existe quatre polyèdres réguliers qui ne sont pas convexes, appelés les solides de Kepler-Poinsot. Ceux-ci ont tous la symétrie icosaédrique et peuvent être obtenus par stellations du dodécaèdre et de l'icosaèdre.

Cuboctaèdre

Icosidodécaèdre

Les prochains polyèdres convexes les plus réguliers après les solides de Platon sont le cuboctaèdre, qui est une rectification (en) du cube et de l'octaèdre, et l'icosidodécaèdre, qui est une rectification du dodécaèdre et de l'icosaèdre (la rectification du polyèdre auto-dual, le tétraèdre, est un octaèdre régulier). Ils sont tous les deux quasi-réguliers ce qui signifie qu'ils sont de sommet et d'arête uniformes et qu'ils ont des faces régulières, mais les faces ne sont pas toutes isométriques (provenant de deux classes différentes). Ils forment deux des treize solides d'Archimède, qui sont des polyèdres uniformes convexes avec une symétrie polyédrique.

Les polyèdres uniformes forment une classe beaucoup plus grande de polyèdres. Ces solides sont de sommets uniformes et on un ou plusieurs types de polygones réguliers (convexes ou étoilés) pour faces. Ceux-ci incluent tous les polyèdres mentionnés ci-dessus avec l'ensemble infini des prismes, l'ensemble infini des antiprismes ainsi que 53 autres formes non-convexes.

Les solides de Johnson sont des polyèdres convexes qui ont des faces régulières mais qui ne sont pas uniformes.

Pavages

Les trois pavages réguliers du plan sont fortement reliés aux solides de Platon. En effet, on peut regarder les solides de Platon comme les cinq pavages réguliers de la sphère. Ceci est effectué en projetant chaque solide sur une sphère concentrique. Les faces projettent sur des polygones sphériques réguliers qui couvrent exactement la sphère. On peut montrer que chaque pavage régulier de la sphère est caractérisé par une paire d'entiers {p, q} avec 1/p + 1/q > 1/2. De même, un pavage régulier du plan est caractérisé par la condition 1/p + 1/q = 1/2. Il existe trois possibilités :

• {4, 4} qui est le pavage carré,
• {3, 6} qui est le pavage triangulaire et
• {6, 3} qui est le pavage hexagonal (dual du pavage triangulaire).

D'une manière similaire, on peut considérer les pavages réguliers sur le plan hyperbolique. Ils sont caractérisés par la condition 1/p + 1/q < 1/2. Il existe un nombre infini de tels pavages.

Dimensions plus élevées

Lorsqu'il y a plus de trois dimensions, les polyèdres se généralisent aux polytopes. Dans le milieu du XIX^e siècle, le mathématicien suisse Ludwig Schläfli découvrit les analogues quadridimensionnels des solides de Platon, appelés les 4-polytopes réguliers convexes. Il existe exactement six de ces figures ; cinq sont analogues aux solides de Platon, tandis que le sixième, le 24-cellules, n'a pas d'analogue en dimension inférieure.

Dans les dimensions plus élevées que quatre, il existe seulement trois polytopes réguliers convexes : le simplexe, l’hypercube et l’hyperoctaèdre. En trois dimensions, ceux-ci coïncident avec le tétraèdre, le cube et l’octaèdre.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Platonic solid » (voir la liste des auteurs).

1. Dans le contexte de cette page, le mot régulier est implicite et généralement omis. Le mot irrégulier est parfois utilisé pour souligner le fait qu'un polyèdre n’est pas régulier, bien qu'il soit encore supposé avoir la même topologie que la forme régulière. D'autres formes topologiques très différentes, telles que le dodécaèdre rhombique qui possède douze faces rhombiques, ou un polyèdre étoilé non-convexe, comme le grand dodécaèdre, ne sont jamais données avec des noms raccourcis.
2. (en) The Scottish solids hoax
3. (de) Eva Sachs, Die fünf platonischen Körper, Berlin, 1917. A.-J. Festugière, Études de philosophie grecque, p. 385.
4. Yvan Monka, Les Solides de Platon.
5. Pour des valeurs approchées plus précises, voir http://villemin.gerard.free.fr/Geometri/Footsphe.htm#remplir.
6. Pour les valeurs approchées de V/V_s, voir (en) http://www.thomasbending.co.uk/puzzles/geometry/spheresolids.htm, Volume of the circumscribed solid.
7. (en) H. S. M. Coxeter, Regular Polytopes, Dover, 1973, 3^e éd. (lire en ligne), p. 46-47.
8. (de) E. Haeckel, Kunstformen der Natur, 1904, rééd. (en) Art forms in nature, Prestel USA, 1998 (ISBN 3-7913-1990-6)
9. (en) Leon Tucker, Mike Reese et Ernest Gary Gygax, Tractics, Guidon Games, 1971 ; 2^de édition par TSR en 1975.
10. Michael Witwer, L'Empire de l'imaginaire : Gary Gygax et la naissance de Dungeons & Dragons, Sycko, 2018 (ISBN 979-10-94206-18-8), p. 93-94.

Voir aussi

Bibliographie

• Platon, Timée (vers 358 av. J.-C.), 55 e-56 c. Trad. L. Brisson, Timée/Critias, Garnier-Flammarion, 3° éd. revue 1996
• Euclide, Éléments (vers 300 av. J.-C.), livre XIII, Euclide, Les Éléments, volume IV, Livre XI-XIII, Géométrie des solides ; trad. du texte par Heiberg et commentaires par Bernard Vitrac. Paris, Presses universitaires de France, 2001, (Bibliothèque d'histoire des sciences), 482 p. (ISBN 2-13-051927-X)

Articles connexes

• Polytope régulier
• Liste des polytopes réguliers (en)
• Livre XIII des Éléments d'Euclide
• Hydrocarbure de Platon - les solides de Platon moléculaires
• Patron (géométrie)
• Libellus de quinque corporibus regularibus de Piero della Francesca
• Trattato d'abaco de Piero della Francesca

Liens externes

• Notices d'autorité :

  • GND
• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Britannica
  • Internetowa encyklopedia PWN
  • Larousse
• (en) platonicsolids.info
• (en) Interactive polyhedra en Java
• (en) Platonic Solids (animation interactive) sur agutie.homestead.com
• (en) Pictures of Platonic Solids (patrons en papier)