Loi inverse-gamma

Inverse-gamma
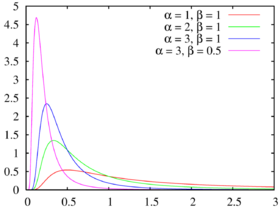
Densité de probabilité
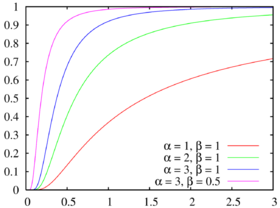
Fonction de répartition
Paramètres	${\displaystyle \alpha >0}$ paramètre de forme (réel) ${\displaystyle \beta >0}$ paramètre d'échelle (réel)
Support	${\displaystyle x\in \left]0;\infty \right[}$
Densité de probabilité	${\displaystyle {\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}x^{-\alpha -1}\exp \left({\frac {-\beta }{x}}\right)}$
Fonction de répartition	${\displaystyle {\frac {\Gamma (\alpha ,\beta /x)}{\Gamma (\alpha )}}\!}$
Espérance	${\displaystyle {\frac {\beta }{\alpha -1}}\!}$ pour ${\displaystyle \alpha >1}$
Mode	${\displaystyle {\frac {\beta }{\alpha +1}}\!}$
Variance	${\displaystyle {\frac {\beta ^{2}}{(\alpha -1)^{2}(\alpha -2)}}\!}$ pour ${\displaystyle \alpha >2}$
Asymétrie	${\displaystyle {\frac {4{\sqrt {\alpha -2}}}{\alpha -3}}\!}$ pour ${\displaystyle \alpha >3}$
Kurtosis normalisé	${\displaystyle 6{\frac {5\,\alpha -11}{(\alpha -3)(\alpha -4)}}\!}$ pour ${\displaystyle \alpha >4}$
Entropie	${\displaystyle \alpha \!+\!\ln(\beta \Gamma (\alpha ))\!-\!(1\!+\!\alpha )\psi (\alpha )}$
Fonction génératrice des moments	${\displaystyle {\frac {2\left(-\beta t\right)^{\!\!{\frac {\alpha }{2}}}}{\Gamma (\alpha )}}K_{\alpha }\left({\sqrt {-4\beta t}}\right)}$
Fonction caractéristique	${\displaystyle {\frac {2\left(-\mathrm {i} \beta t\right)^{\!\!{\frac {\alpha }{2}}}}{\Gamma (\alpha )}}K_{\alpha }\left({\sqrt {-4\mathrm {i} \beta t}}\right)}$
modifier

Dans la théorie des probabilités et en statistiques, la distribution inverse-gamma est une famille de lois de probabilité continues à deux paramètres sur la demi-droite des réels positifs. Il s'agit de l'inverse d'une variable aléatoire distribuée selon une distribution Gamma.

Caractérisation

Densité de probabilité

La densité de probabilité de la loi inverse-gamma est définie sur le support ${\displaystyle x>0}$ par:

${\displaystyle f(x;\alpha ,\beta )={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}(1/x)^{\alpha +1}\exp \left(-\beta /x\right)}$

où ${\displaystyle \alpha }$ est un paramètre de forme et ${\displaystyle \beta }$ un paramètre d'intensité, c'est-à-dire l'inverse d'un paramètre d'échelle.

Fonction de répartition

La fonction de répartition est la fonction gamma régularisée :

${\displaystyle F(x;\alpha ,\beta )={\frac {\Gamma (\alpha ,\beta /x)}{\Gamma (\alpha )}}\!}$

où le numérateur est la fonction gamma incomplète et le dénominateur est la fonction gamma.

Distributions associées

• Si ${\displaystyle X\sim {\mbox{Inv-Gamma}}(\alpha ,\beta )}$ et ${\displaystyle \alpha ={\frac {\nu }{2}},\beta ={\frac {1}{2}}}$ alors ${\displaystyle X\sim {\mbox{Inv-chi-square}}(\nu )\,}$ est une loi inverse-χ²;
• Si ${\displaystyle X\sim {\mbox{Inv-Gamma}}(k,\theta )\,}$, alors ${\displaystyle 1/X\sim {\mbox{Gamma}}(k,1/\theta )\,}$ la loi Gamma de paramètre de forme ${\displaystyle k}$ et de paramètre d'échelle ${\displaystyle 1/\theta }$ (ou de manière équivalente, d'intensité ${\displaystyle \theta }$);
• Une généralisation multivariée de la loi inverse-gamma est la loi de Wishart inverse.

Obtention à partir de la loi Gamma

La densité de la loi Gamma est

${\displaystyle f(x)=x^{k-1}{\frac {\mathrm {e} ^{-x/\theta }}{\theta ^{k}\,\Gamma (k)}}}$

et définissons la transformation ${\displaystyle Y=g(X)={\frac {1}{X}}}$. La densité de la transformée est alors

${\displaystyle f_{Y}(y)=f_{X}\left(g^{-1}(y)\right)\left|{\frac {\mathrm {d} }{\mathrm {d} y}}g^{-1}(y)\right|}$

${\displaystyle ={\frac {1}{\theta ^{k}\Gamma (k)}}\left({\frac {1}{y}}\right)^{k-1}\exp \left({\frac {-1}{\theta y}}\right){\frac {1}{y^{2}}}}$

${\displaystyle ={\frac {1}{\theta ^{k}\Gamma (k)}}\left({\frac {1}{y}}\right)^{k+1}\exp \left({\frac {-1}{\theta y}}\right)}$

${\displaystyle ={\frac {1}{\theta ^{k}\Gamma (k)}}y^{-k-1}\exp \left({\frac {-1}{\theta y}}\right)}$

Remplaçant ${\displaystyle k}$ par ${\displaystyle \alpha }$, ${\displaystyle \theta ^{-1}}$ par ${\displaystyle \beta }$ et enfin ${\displaystyle y}$ par ${\displaystyle x}$ donne la densité donnée plus haut :

${\displaystyle f(x)={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}x^{-\alpha -1}\exp \left({\frac {-\beta }{x}}\right)}$

Apparitions

• La loi du temps de premier contact (en) dans un processus de Wiener est une distribution de Lévy, qui est une loi inverse-gamma de paramètre ${\displaystyle \alpha =0,5}$[1]

Références

1. (en) Mike Ludkovski, « Math 526: Brownian Motion Notes », UC Santa Barbara, 2007, p. 5-6