Courbe de Peano

Giuseppe Peano vers 1910.

En mathématiques, la courbe de Peano est le premier exemple découvert de courbe remplissante, c'est-à-dire une courbe plane paramétrée par une fonction continue sur l'intervalle unité [0, 1] et surjective dans le carré [0, 1]×[0, 1] ; autrement dit, la courbe passe par chaque point du carré : elle « remplit l'espace ».

En particulier, la courbe de Peano est une fractale : bien que formée d'une simple ligne, elle est de dimension 2.

Cette courbe est nommée en l'honneur de Giuseppe Peano qui l'a découverte.

Historique

Dans un article de 1890[1] Giuseppe Peano décrit une courbe auto-intersectante qui passe par tous les points de la surface du carré unité. En construisant une surjection de l'intervalle réel unité vers le carré unité du plan, il illustre un résultat de Georg Cantor qui, en 1877, avait établi que le carré a la puissance du continu, c'est-à-dire le même cardinal que l'intervalle. La nouveauté est que la surjection construite par Peano est continue : on peut l'interpréter comme une courbe paramétrée.

La clé passe par l'élaboration d'une courbe nulle part différentiable. Toutes les courbes rencontrées jusqu'alors étaient différentiables par parties (elles avaient une dérivée continue sur chaque intervalle). En 1872, Karl Weierstrass avait bien décrit une fonction qui était continue en tout point mais différentiable en aucun point. Mais aucune de ces courbes ne pouvait remplir le carré unité. La courbe de Peano, à la fois nulle part différentiable et remplissant le plan, était donc fortement contre-intuitive.

Peano utilise l'existence d'un développement en base trois pour tout nombre réel. Dans l'ensemble des suites à valeurs dans {0,1,2}, il construit une correspondance entre la suite ${\displaystyle T=(a_{n})_{n\in \mathbb {N} ^{*}}}$ et le couple de suites ${\displaystyle (X,Y)=((b_{n})_{n\in \mathbb {N} ^{*}},(c_{n})_{n\in \mathbb {N} ^{*}})}$ de la manière suivante :

• ${\displaystyle b_{n}=a_{2n-1}{\text{ ou }}2-a_{2n-1}}$ selon que la somme des termes de rang pair de la suite ${\displaystyle (a_{n})}$ : ${\displaystyle \sum _{1\leq k\leq n-1}a_{2k}}$ est paire ou impaire (par convention, la somme vide ${\displaystyle \sum _{1\leq k\leq 0}a_{2k}}$ est nulle donc paire, donc ${\displaystyle b_{1}=a_{1}}$)
• ${\displaystyle c_{n}=a_{2n}{\text{ ou }}2-a_{2n}}$ selon que la somme des termes de rang impair de la suite ${\displaystyle (a_{n})}$ : ${\displaystyle \sum _{k=1}^{n}a_{2k-1}}$ est paire ou impaire.

Quatre itérations de la courbe de Peano.

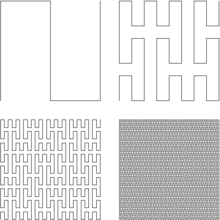À chaque suite, il associe le réel dont la suite est un développement en base 3

${\displaystyle t=0,a_{1}a_{2}\cdots a_{n}\cdots =\sum _{k=1}^{+\infty }a_{k}3^{-k},\qquad x=0,b_{1}b_{2}\cdots b_{n}\cdots =\sum _{k=1}^{+\infty }b_{k}3^{-k},\qquad y=0,c_{1}c_{2}\cdots c_{n}\cdots =\sum _{k=1}^{+\infty }c_{k}3^{-k}.}$

Il démontre que la correspondance qui, au réel t, associe le couple de réels (x, y) est bien définie (c'est-à-dire que si t a deux développements en base 3, comme 1/3 = 0,1000… = 0,0222…, alors les deux couples (x, y) correspondants sont identiques[1]) et que cette application de [0,1] dans [0,1]×[0,1] est continue, surjective, mais non injective (un couple (x, y) correspond à 2 ou 4 valeurs de t si x, ou y, ou les deux, ont deux développements[1]).

L'article de Peano ne contient pas d'illustration. Une observation des troncatures des suites ${\displaystyle t}$, ${\displaystyle x}$ et ${\displaystyle y}$ au rang 2, conduirait à la construction successive des points de coordonnées (0,0), (0,1/3), (0,2/3), (1/3,2/3), (1/3,1/3), (1/3,0), (2/3,0), (2/3,1/3), (2/3,2/3) qui, joints par des segments de droites donnent une courbe analogue à l'étape 1 de l'illustration ci-contre. Pour les suites tronquées au rang 4, on trace une courbe analogue à l'itération 2 ci-contre, commençant au point de coordonnées (0,0) et aboutissant au point de coordonnées (8/9,8/9), etc.

De nombreux autres exemples de courbes remplissantes (du plan ou de l'espace) furent construits sur ce modèle, par exemple la courbe de Hilbert ; certaines possèdent des propriétés meilleures encore que celle de Peano, comme la courbe de Lebesgue, qui est en outre presque partout dérivable.

Propriétés

• Contrairement à ces approximantes, présentées comme des courbes qui ne se recoupent pas[2], la courbe de Peano est auto-intersectante et correspond donc à une fonction non injective (par exemple ${\displaystyle (x;y)({\frac {1}{9}})=(x;y)({\frac {5}{9}})=({\frac {1}{3}};{\frac {1}{3}})}$). Une bijection continue d'un segment dans un carré est d'ailleurs impossible, en effet une telle application serait un homéomorphisme[3], or le complémentaire d'un point du carré est toujours connexe, alors que son image réciproque serait en général formée de deux segments disjoints.
• La courbe de Peano est 1/2-höldérienne. Ce « 1/2 » est optimal, c'est-à-dire que la constante de Hölder d'une surjection höldérienne de [0, 1] sur [0, 1]^2 est toujours inférieure ou égale à 1/2 : cf. « Dimension et fonctions a-höldériennes ».

Références

1. G. Peano, « Sur une courbe, qui remplit toute une aire plane », Math. Ann., vol. 36,‎ 1890, p. 157-160 (lire en ligne).
2. Selon Benoît Mandelbrot (« Des monstres de Cantor et Peano à la géométrie fractale de la nature », dans Penser les mathématiques, Séminaire de Jean Dieudonné, Maurice Loi et René Thom, 1982, p. 238/4), la coutume interdit aux approximantes de Peano de s'intersecter.
3. Plus généralement, toute bijection continue d'un compact vers un espace séparé est un homéomorphisme.

Voir aussi

Articles connexes

• Liste de fractales par dimension de Hausdorff
• Théorème de Hahn-Mazurkiewicz
• Théorème de l'invariance du domaine

Bibliographie

• (en) Hans Sagan, Space-Filling Curves, Berlin/New York, Springer-Verlag, 1994, 193 p. (ISBN 0-387-94265-3)
• (en) Benoît Mandelbrot, The Fractal Geometry of Nature, Freeman, 1982, 468 p. (ISBN 978-0-7167-1186-5), « Harnessing the Peano Monster Curves »

Liens externes

• Courbe de Peano sur mathcurve.com
• (en) Applets Java sur cut-the-knot :
  • Peano Plane Filling Curves
  • Hilbert's and Moore's Plane Filling Curves
  • All Peano Plane Filling Curves