الرياضيات ، دالة قوس الجيب [ 1] [ 2] [ 3] بالإنجليزية : Arcsine ) لعدد حقيقي المحصور بين –1 و 1 هي الدالة العكسية لدالة الجيب ، مستقرها هو
[
−
π
2
,
π
2
]
{\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}
الراديان .
الدالة التي ترفق بكل عدد حقيقي المحصور بين –1 و 1 قيمة قوس جيب الخاص به يرمز لها بـ arcsin أو sin -1 الدالة العكسية لدالة الجيب المثلثية المقتصرة إلى المجال
[
−
π
2
,
π
2
]
{\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}
في المَعْلم الديكارتي المتعامد الوَحْديّ للمستوي، يتم الحصول على التمثيل البياني لدالة قوس جيب الزاوية انطلاقا من التمثيل البياني لدالة الجيب المقتصرة إلى المجال
[
−
π
2
,
π
2
]
{\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}
انعكاس حول المحور ذو المعادلة y = x
دالة الجيب العكسية تقبل الإشتقاق على المجال ]–1, 1[ ودالتها المشتقة هي:
arcsin
′
x
=
1
1
−
x
2
{\displaystyle \arcsin 'x={\frac {1}{\sqrt {1-x^{2}}}}}
يمكننا كتابة مشتقة الدالة بهذه الصيغة:
(
arcsin
x
)
′
=
d
d
x
arcsin
x
{\displaystyle (\arcsin x)'={d \over dx}\arcsin x}
نضع
θ
=
arcsin
x
{\displaystyle \theta =\arcsin x}
d
θ
d
sin
θ
=
d
θ
d
θ
cos
θ
=
1
cos
θ
=
1
1
−
sin
2
θ
=
1
1
−
x
2
{\displaystyle {\frac {d\theta }{d\sin \theta }}={\frac {d\theta }{d\theta \cos \theta }}={\frac {1}{\cos \theta }}={\frac {1}{\sqrt {1-\sin ^{2}\theta }}}={\frac {1}{\sqrt {1-x^{2}}}}}
يمكننا تمثيل الدالة بواسطة متسلسلة تايلور :
إذا كانت
|
z
|
≤
1
{\displaystyle |z|\leq 1}
arcsin
z
=
z
+
1
2
⋅
z
3
3
+
1
⋅
3
2
⋅
4
⋅
z
5
5
+
1
⋅
3
⋅
5
2
⋅
4
⋅
6
⋅
z
7
7
+
…
=
∑
n
=
0
∞
(
2
n
−
1
)
!
!
(
2
n
)
!
!
⋅
z
2
n
+
1
2
n
+
1
=
∑
n
=
0
∞
(
2
n
n
)
z
2
n
+
1
4
n
(
2
n
+
1
)
.
{\displaystyle {\begin{aligned}\arcsin z&=z+{\frac {1}{2}}\cdot {\frac {z^{3}}{3}}+{\frac {1\cdot 3}{2\cdot 4}}\cdot {\frac {z^{5}}{5}}+{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\cdot {\frac {z^{7}}{7}}+\dots \\&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}\cdot {\frac {z^{2n+1}}{2n+1}}\\&=\sum _{n=0}^{\infty }{\frac {{\binom {2n}{n}}z^{2n+1}}{4^{n}(2n+1)}}.\end{aligned}}}
حيث
(
n
)
!
!
{\displaystyle (n)!!}
عاملي ثنائي .
برهان
متسلسلة تايلور للدالة المستقة هي:
arcsin
′
(
z
)
=
(
1
−
z
2
)
−
1
2
=
1
+
(
−
1
2
)
(
−
z
2
)
+
(
−
1
2
)
(
−
3
2
)
2
(
−
z
2
)
2
+
(
−
1
2
)
(
−
3
2
)
(
−
5
2
)
2
⋅
3
(
−
z
2
)
3
+
⋯
=
1
+
1
2
z
2
+
1
⋅
3
2
⋅
4
z
4
+
1
⋅
3
⋅
5
2
⋅
4
⋅
6
z
6
+
…
,
{\displaystyle {\begin{aligned}\arcsin '(z)&=(1-z^{2})^{-{\frac {1}{2}}}\\&=1+\left(-{\frac {1}{2}}\right)(-z^{2})+{\frac {\left(-{\frac {1}{2}}\right)\left(-{\frac {3}{2}}\right)}{2}}(-z^{2})^{2}+{\frac {\left(-{\frac {1}{2}}\right)\left(-{\frac {3}{2}}\right)\left(-{\frac {5}{2}}\right)}{2\cdot 3}}(-z^{2})^{3}+\cdots \\&=1+{\frac {1}{2}}z^{2}+{\frac {1\cdot 3}{2\cdot 4}}z^{4}+{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}z^{6}+\dots ,\end{aligned}}}
بمكاملتها نتحصل على المتسلسلة غير المنتهية للدالة.
يمكن كتابة هذه الدالة على شكل التكامل غير المحدد :
arcsin
x
=
∫
0
x
1
1
−
t
2
d
t
{\displaystyle \arcsin x=\int _{0}^{x}{\frac {1}{\sqrt {1-t^{2}}}}dt}
arccos x (بالأزرق) و arcsin x (بالأحمر) يتم الحصول على المشتق العكسي لدالة قوس الجيب عن طريق التكامل بالتجزئة :
∫
arcsin
x
d
x
=
x
arcsin
x
+
1
−
x
2
+
C
{\displaystyle \int \arcsin x\,\mathrm {d} x=x\arcsin x+{\sqrt {1-x^{2}}}+C}
من أجل كل عدد حقيقي x –1 و 1 :
arccos
x
+
arcsin
x
=
π
2
{\displaystyle \arccos x+\arcsin x={\frac {\pi }{2}}}
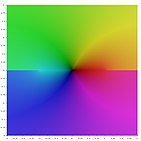
التمثيل البياني اللوني للدالة
arcsin
z
{\displaystyle \arcsin z}
يمكننا التعبير عن دالة قوس الجيب باستخدام اللوغاريتم العقدي :
arcsin
x
=
−
i
ln
(
i
x
+
1
−
x
2
)
{\displaystyle \arcsin x=-i\ln \left(ix+{\sqrt {1-x^{2}}}\right)}




![{\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54381f086ac9ffe8306d413f813abcb616e95dee)


![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)















