1 − 2 + 3 − 4 + ⋯

15.000 jumlah parsial pertama dari 0 + 1 − 2 + 3 − 4 + ⋯. Pada grafik ini, bilangan bulat negatif berada di bagian kiri sedangkan bilangan bulat positif berada di bagian kanan.

Dalam matematika, 1 − 2 + 3 − 4 + ⋯ adalah deret tak hingga yang suku-sukunya merupakan bilangan bulat positif yang berurutan. Di samping itu, setiap bilangan bulat tersebut diberi tanda plus dan minus secara bergantian sehingga membentuk deret selang-seling. Dengan menggunakan notasi penjumlahan sigma, jumlah m suku pertama deret tersebut dapat dinyatakan sebagai $${\displaystyle \sum _{n=1}^{m}n(-1)^{n-1}.}$$

Deret di atas divergen. Dengan kata lain, barisan dari jumlah parsial deret tersebut, (1, −1, 2, −2, 3, ...), tidak menuju limit yang pasti. Meskipun demikian, pada pertengahan abad ke-18, Leonhard Euler menemui sebuah kejanggalan: $${\displaystyle 1-2+3-4+\cdots ={\frac {1}{4}}.}$$

Penjelasan yang dianggap ketat secara matematis mengenai kejanggalan ini baru dapat diperoleh beberapa waktu kemudian. Rincinya, per tahun 1890, beberapa matematikawan, seperti Ernesto Cesàro, dan Émile Borel, mulai menyelidiki berbagai metode penjumlahan, termasuk pembaharuan baru atas metode Euler, yang terdefinisi baik agar dapat menentukan nilai deret-deret divergen. Sebagian besar metode penjumlahan tersebut menetapkan nilai atas deret 1 − 2 + 3 − 4 + ... sebagai 14. Salah satu metode yang tidak dapat menentukan nilai deret tersebut adalah penjumlahan Cesàro. Oleh karena itu, diperlukan metode yang sedikit lebih baik, seperti penjumlahan Abel.

Deret 1 − 2 + 3 − 4 + ... memiliki hubungan erat dengan deret Grandi, 1 − 1 + 1 − 1 + .... Oleh karena itu, Euler mengelompokkan keduanya sebagai kasus khusus dari deret umum 1 − 2^n + 3^n − 4^n + ..., berturut-turut n = 1 dan n = 0 untuk masing-masing deret. Selain itu, deret 1 − 2 + 3 − 4 + ... juga berhubungan dengan masalah Basel. Karena hubungan ini, Euler meneliti deret tersebut untuk mengkaji bentuk lain masalah terkait. Penelitian ini kemudian mengarah pada persamaan fungsional yang sekarang dikenal sebagai fungsi eta Dirichlet dan fungsi zeta Riemann.

Kedivergenan

Suku-suku (1, −2, 3, −4, ...) pada deret 1 − 2 + 3 − 4 + ... tidak mendekati 0. Oleh karena itu, berdasarkan uji suku, deret tersebut dinyatakan sebagai divergen. Kedivergenan juga dapat ditunjukkan secara langsung dari definisi deret konvergen. Detailnya, suatu deret tak hingga dikatakan konvergen jika dan hanya jika barisan dari jumlah parsialnya konvergen pada sebuah limit. Dalam hal ini, limitnya adalah nilai deret tak hingga tersebut. Untuk menunjukannya, jumlah parsial dari 1 − 2 + 3 − 4 + ... adalah:[1]

1,

1 − 2 = −1,
1 − 2 + 3 = 2,
1 − 2 + 3 − 4 = −2,
1 − 2 + 3 − 4 + 5 = 3,
1 − 2 + 3 − 4 + 5 − 6 = −3,

...

Barisan dari penjumlahan parsial menunjukkan bahwa deret tersebut tidak konvergen ke suatu bilangan tertentu. Dengan kata lain, untuk sembarang x yang ditetapkan sebagai limit, terdapat suatu titik yang semua jumlah parsialnya berada di luar interval [x−1, x+1]. Dengan demikian, 1 − 2 + 3 − 4 + ... divergen.

Karena setiap barisan atau hasil dari penjumlahan parisal tersebut dapat dipasangkan dengan elemen himpunan bilangan bulat, hal ini menunjukkan ketercacahan ${\displaystyle \mathbb {Z} }$. Dalam artian lain, jumlah parsial tersebut mencakup setiap bilangan bulat tepat satu kali. Bahkan, angka nol apabila bagian kosong diikutkan.[2]

Heuristik untuk penjumlahan

Stabilitas dan linearitas

Karena suku 1, −2, 3, −4, 5, −6, ... mengikuti pola yang sederhana, deret 1 − 2 + 3 − 4 + ... dapat dimanipulasi dengan memindahkan letak setiap suku sedemikian rupa sehingga memperoleh sebuah nilai. Singkatnya, jika deret tersebut dapat ditulis menjadi s = 1 − 2 + 3 − 4 + ... dengan s adalah sebuah bilangan, manipulasi pada deret tersebut akan memperoleh nilai s = ¼:[3]

$${\displaystyle {\begin{alignedat}{5}4s&=&&(1-2+3-\cdots )\ \ &&{}+(1-2+3-4+\cdots )&&{}+(1-2+3-4+\cdots )&&{}+(1-2+3-4+\cdots )\\&=&&(1-2+3-\cdots )&&+1{}+(-2+3-4+\cdots )\ \ &&{}+1+(-2+3-4+\cdots )\ \ &&{}+1-2+(3-4+\cdots )\\&=\ 1+{}&&(1-2+3-\cdots )&&{}+(-2+3-4+\cdots )&&{}+(-2+3-4+\cdots )&&{}+(3-4+5-\cdots )\\&=\ 1+{}[\ &&(1-2-2+3)&&{}+(-2+3+3-4)&&{}+(3-4-4+5)&&{}+\cdots \ ]\\&=\ 1+{}[\ &&0+0+0+\cdots \ ]\\4s&=\ 1\end{alignedat}}}$$

Dengan menambahkan empat salinan deret 1 − 2 + 3 − 4 + ··· sekaligus memindahkan letak setiap suku sedemikian rupa, penjumlahan akan menghasilkan nilai 1. Di samping itu, masing-masing ruas kiri dan kanan menunjukkan penjumlahan dua salinan deret 1 − 2 + 3 − 4 + ··· yang menghasilkan deret 1 − 1 + 1 − 1 + ···.

Jadi, ${\displaystyle s={\frac {1}{4}}}$.

Meskipun 1 − 2 + 3 − 4 + ... tidak dapat dijumlahkan sesuai pada umumnya, persamaan s = 1 − 2 + 3 − 4 + ... = ¼ dapat dikatakan sebagai jawaban paling logis jika deret seperti itu harus diberi nilai. Sehubungan dengan itu, bentuk generalisasi untuk menentukan nilai "penjumlahan" deret divergen disebut sebagai metode penjumlahan atau metode keterjumlahan. Untuk jenisnya, metode tersebut memiliki banyak ragam. Biasanya, setiap ragam harus memiliki beberapa sifat dari penjumlahan biasa. Di luar hal ini, apabila diteliti lagi, manipulasi yang dijelaskan di atas sebenarnya membuktikan suatu hal. Pada konteks ini, apabila deret 1 − 2 + 3 − 4 + ... ditentukan jumlahnya menggunakan metode keterjumlahan yang linear dan stabil, jumlah deret tersebut akan bernilai ¼.[4] Lebih lanjut, $${\displaystyle {\begin{alignedat}{5}2s&=&&(1-2+3-4+\cdots )\ \ &&{}+(1-2+3-4+5-\cdots )\\&=&&1{}+(-2+3-4+\cdots )\ \ &&{}+1-2+(3-4+5-\cdots )\\&=\ 0+{}&&(-2+3-4+\cdots )&&{}+(3-4+5-\cdots )\\&=\ 0+{}[\ &&(-2+3)\quad {}+(3-4)&&{}+(-4+5)\quad +\cdots \ ]\\2s&=\ &&1-1+1-1+\cdots \end{alignedat}}}$$

metode tersebut pasti menjumlahkan deret Grandi, yaitu 1 − 1 + 1 − 1 + ... = ½.[4]

Hasil kali Cauchy

Pada tahun 1891, Ernesto Cesàro menyatakan bahwa deret divergen dapat dijelaskan dengan menyeluruh melalui kalkulus. Dalam hal ini, ia memperlihatkan bahwa, "Saya telah menulis (1 − 1 + 1 − 1 + ...)^2 = 1 − 2 + 3 − 4 + ... dan menyatakan kedua sisinya sama dengan ¼."[5] Cesàro mengatakan bahwa persamaan tersebut merupakan penerapan dari teorema yang ia telah perkenalkan pada tahun sebelumnya. Teorema tersebut merupakan yang pertama dalam sejarah mengenai penjumlahan deret divergen (lihat disini untuk penjelasan teoremanya).[1] Secara matematis, kunci utama dari teorema tersebut ada pada konsep perkalian Cauchy. Sebagai contoh, apabila diterapkan pada kasus yang diperlihatkan oleh Cesàro, deret 1 − 2 + 3 − 4 + .... dapat dinyatakan sebagai perkalian (konvolusi diskret) atas 1 − 1 + 1 − 1 + ... dengan 1 − 1 + 1 − 1 + ....

Dalam praktiknya, perkalian Cauchy antara dua deret tak terhingga dapat dilakukan walaupun kedua deret tersebut divergen. Pada kasus a_n = b_n = (−1)^n, suku-suku hasil kali Cauchy dapat dituliskan dengan deret diagonal $${\displaystyle {\begin{aligned}c_{n}&=\sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\&=\sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{aligned}}}$$

Maka deret hasil kalinya menjadi $${\displaystyle \sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots .}$$

Jadi, dari perhitungan di atas, dapat diambil kesimpulan bahwa setiap metode penjumlahan yang menjumlahkan deret 1 − 1 + 1 − 1 + ... menjadi 1/2 akan menghasilkan nilai 1/4 untuk deret 1 − 2 + 3 − 4 + dst. apabila dikonvolusi diskret (dikalikan dengan Cauchy). Per penjelasan pada bagian sebelumnya, hal ini menyiratkan kesetaraan antara keterjumlahan 1 − 1 + 1 − 1 + ... dan 1 − 2 + 3 − 4 + ... apabila metode yang digunakan bersifat linear, stabil, dan dapat dikalikan dengan perkalian Cauchy.

Perhitungan di atas merupakan salah satu bentuk dari penggunaan teorema Cesàro. Apabila teorema Cesàro digunakan untuk menghitung jumlah deret 1 − 1 + 1 − 1 + ... yang berkelas (C, 1), dapat digunakan bentuk biasa. Di sisi lain, deret 1 − 2 + 3 − 4 + ... memerlukan bentuk teorema Cesàro yang lebih kuat.[6] Kelas penjumlahan Cesàro yang merujuk untuk deret tersebut adalah (C, 2). Dalam menghitung nilai kedua deret tersebut, dapat dilakukan seperti cara di atas karena semua bentuk teorema Cesàro bersifat linear dan stabil.[7]

Metode khusus

Cesàro dan Hölder

Data tentang jumlah (H, 2) yang menghasilkan nilai ¼

Untuk mencari nilai (C, 1) dari deret 1 − 2 + 3 − 4 + ... dengan menggunakan penjumlahan Cesàro, diperlukan penghitungan rata-rata aritmetika dari jumlah parsial deret tersebut. Jumlah parsialnya adalah:

1, −1, 2, −2, 3, −3, ...,

dan rata-rata aritmatika dari jumlah parsial ini adalah:

1, 0, ⅔, 0, ⅗, 0, 4⁄7, ....

Urutan rata-rata ini tidak konvergen. Oleh karena itu, deret 1 − 2 + 3 − 4 + ... tidak dapat ditentukan nilainya dengan metode penjumlahan Cesàro .

Ada dua bentuk terkenal atas perluasan metode penjumlahan Cesàro. Dalam hal ini, bentuk yang sederhana adalah metode (H, n) dengan n bilangan asli. Pada kasus di atas, penjumlahan Cesàro memiliki bentuk (H, 1). Di sisi lain, bentuk n = 2 akan mengulangi penghitungan rata-rata. Apabila diteliti lagi, urutan di atas memiliki rata-rata ganjil yang konvergen ke ½. Sementara itu, semua rata-rata genapnya sama dengan 0. Karena itu, ketika menerapkan bentuk n = 2 atau rata-rata atas rata-rata konvergen, rata-rata dari 0 dan ½ akan menghasilkan nilai sebesar ¼.[8] Jadi, 1 − 2 + 3 − 4 + ... adalah (H, 2) dan bernilai sebesar ¼.

Huruf "H" adalah inisial atas nama Otto Hölder. Ia yang pertama kali membuktikan pada tahun 1882 sesuatu yang sekarang dianggap oleh matematikawan sebagai hubungan antara penjumlahan Abel dan (H, n). Pada pembuktian tersebut, deret 1 − 2 + 3 − 4 + ... adalah contoh pertamanya.[9] Rincinya, fakta bahwa ¼ adalah nilai dari deret 1 − 2 + 3 − 4 + ... menjamin bahwa itu adalah jumlah Abel. Hal ini akan dibuktikan langsung di bagian bawah.

Perluasan penjumlahan Cesàro yang umum dirumuskan adalah bentuk (C, n). Secara matematis, bentuk tersebut dan (H, n) terbukti selalu memberikan hasil yang sama. Akan tetapi, keduanya mempunyai latar belakang sejarah yang berbeda. Latar belakang (C, n) sendiri bermula pada tahun 1887 ketika Cesàro menggunakan metode penjumlahan yang mirip dengan (C, n), tetapi ia hanya memberikan sedikit contoh. Salah satu contoh yang ia berikan yakni penjumlahan 1 − 2 + 3 − 4 + ... menjadi ¼. Namun, metode tersebut belum ia definisikan secara formal. Akhirnya, pada tahun 1890, ia secara formal mendefinisikan metode (C, n) untuk membantu menyatakan salah satu teoremanya. Detailnya, teorema tersebut menyatakan bahwa perkalian Cauchy atas deret terjumlahkan (C, n) dan (C, m) adalah sama dengan deret terjumlahkan (C, m + n + 1).[10]

Penjumlahan Abel

Beberapa bagian dari 1 − 2x + 3x^2 + ...= 1/(1 + x)^2 dengan batas 1.

Pada tahun 1749, Leonhard Euler mengakui bahwa deret 1 − 2 + 3 − 4 + ... divergen. Walaupun begitu, ia tetap menjumlahkannya:

... ketika dikatakan bahwa jumlah deret 1 − 2 + 3 − 4 + 5 − 6 dst. bernilai ¼, hal ini tampak janggal. Karena ketika menjumlahkan 100 suku pada deret ini, kita mendapatkan −50. Di samping itu, jumlah dari 101 suku menghasilkan +51. Hasil ini sangat berbeda dengan ¼ dan menjadi lebih besar jika jumlah sukunya ditambah. Oleh karena itu, kata jumlah perlu diberi arti yang lebih luas seperti yang saya perhatikan di hasil-hasil perhitungan sebelumnya ...[11]

Euler beberapa kali mengusulkan perluasan atas kata "jumlah". Dalam kasus 1 − 2 + 3 − 4 + ..., gagasannya mirip dengan penjumlahan Abel:

... tidak diragukan lagi bahwa jumlah deret 1 − 2 + 3 − 4 + 5 dst. adalah ¼. Hal ini merupakan hasil dari perluasan 1/(1+1)^2 yang nilainya tidak dapat disangkal ¼. Nilai janggal seperti ini menjadi lebih jelas dengan mempertimbangkan deret pangkat 1 − 2x + 3x^2 − 4x^3 + 5x^4 − 6x^5 + &c. yang diperoleh saat memperluas ekspresi matematis 1/(1+x)^2. Perluasan ini akan sama dengan deret 1 − 2 + 3 − 4 + 5... setelah kita menetapkan x = 1.[12]

Setidaknya, untuk nilai absolut |x| < 1, Euler benar dalam hal ini $${\displaystyle 1-2x+3x^{2}-4x^{3}+\cdots ={\frac {1}{(1+x)^{2}}}.}$$ Untuk membuktikan kesamaan ekspresi di atas, perlu menggunakan perluasan Taylor pada ruas kanan atau pembagian bersusun polinomial. Pada ruas kiri, perlu menerapkan tata cara heuristik seperti bagian sebelumnya. Dalam hal ini, (1 + x) dikalikan dua kali atau deret geometri 1 − x + x^2 − .... dikuadratkan. Selain itu, Euler juga menyarankan untuk menurunkan suku deret geometri tersebut satu per satu sebagai salah satu alternatif.[13]

Dalam pandangan modern, fungsi generatif 1 − 2x + 3x^2 − 4x^3 + ... tidak dapat didefinsikan sebagai suatu fungsi pada x = 1. Oleh karena itu, angka tersebut tidak dapat disubstitusikan begitu saja pada fungsi generatif terkait. Walaupun demikian, karena fungsinya terdefinisi untuk semua |x| < 1, limit ketika x mendekati 1 masih dapat diambil. Hal ini adalah definisi dari jumlah Abel: $${\displaystyle \lim _{x\rightarrow 1^{-}}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}.}$$

Euler dan Borel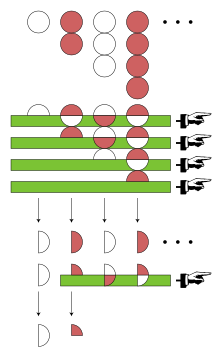

Transformasi Euler menghasilkan ½ − ¼. Pada gambar ini, nilai positif ditampilkan dalam warna putih sedangkan nilai negatif ditampilkan dalam warna coklat. Selain itu, pergeseran serta penghilangan suatu nilai (pengurangan) ditampilkan dalam warna hijau.

Euler menerapkan teknik lain pada deret tersebut, yakni transformasi Euler. Transformasi tersebut merupakan salah satu penemuannya. Untuk menghitung transformasi Euler, dimulai dengan barisan suku positif yang membentuk deret bolak-balik 1 − 2 + 3 − 4 + .... Dalam hal ini, barisan 1, 2, 3, 4, .... Elemen pertama barisan ini diberi label a₀.

Selanjutnya, diperlukan barisan selisih maju dari 1, 2, 3, 4, dst. Dalam hal ini, hanya 1, 1, 1, 1, dst. Elemen pertama barisan ini diberi label Δa₀. Di samping selisih maju, transformasi Euler juga bergantung pada selisih dari selisih. Biasanya, hal tersebut akan membutuhkan iterasi (pengulangan) yang banyak. Namun, semua selisih maju antara 1, 1, 1, 1, ... adalah 0. Oleh karena itu, tidak diperlukan iterasi lagi. Lebih lanjut, transformasi Euler dari 1 − 2 + 3 − 4 + ... akan didapatkan sebagai $${\displaystyle {\frac {1}{2}}a_{0}-{\frac {1}{4}}\Delta a_{0}+{\frac {1}{8}}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}}-{\frac {1}{4}}.}$$

Dalam terminologi modern, dapat dikatakan bahwa deret 1 − 2 + 3 − 4 + ... terjumlahkan oleh metode Euler dan bernilai ¼..

Sehubungan dengan itu, apabila penjumlahan Euler dapat menghasilkan nilai atas deret tersebut, penjumlahan Borel juga. Secara hasil, nilai penjumlahannya akan sama.[14]

Pemisahan skala

Saichev dan Woyczyński sampai pada 1 − 2 + 3 − 4 + ... = ¼ dengan hanya menerapkan dua prinsip: relaksasi yang sangat kecil dan pemisahan skala. Dengan kedua prinsip tersebut, mereka kemudian mendefinisikan kelompok besar "metode penjumlahan φ". Kelompok tersebut merupakan sekumpulan deret bernilai ¼:

• Jika φ(x) adalah suatu fungsi yang turunan pertama dan keduanya kontinu dan dapat diintegralkan pada (0, ∞) sehingga φ(0) = 1 dan limit dari φ(x) dan xφ(x) pada +∞ adalah sama-sama 0, maka[15] $${\displaystyle \lim _{\delta \rightarrow 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}}.}$$

Deret di atas merupakan perluasan atas penjumlahan Abel. Tepatnya, deret tersebut diperoleh dengan menyubtitusi φ(x) = exp(−x) pada jumlah Abel. Untuk ekspresi keseluruhannya, dapat dibuktikan dengan memasangkan suku-suku dalam deret tersebut hingga batas m. Kemudian, mengubah deret tersebut menjadi integral Riemann. Pada bagian integral Riemann, penyelesaian deret 1 − 1 + 1 − 1 + ... menerapkan teorema nilai purata, tetapi dalam kasus ini diperlukan bentuk Lagrange yang lebih kuat atas teorema Taylor.

Generalisasi

Kutipan dari hal. 233 E212 — Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum. Pada kutipan ini, Euler menjumlahkan deret serupa, ca 1755.

Hasil kali Cauchy rangkap tiga dari 1 − 1 + 1 − 1 + ... adalah 1 − 3 + 6 − 10 + dst. Hasil kali tersebut memiliki suku bilangan segitiga yang berselang-seling. Untuk nilainya, berjumlah ⅛ apabila dihitung menggunakan jumlah Abel atau Euler.[16] Sementara itu, hasil kali Cauchy rangkap empat dari 1 − 1 + 1 − 1 + ... adalah 1 − 4 + 10 − 20 + dst. Hasil kali tersebut memiliki suku bilangan piramida yang berselang-seling. Untuk nilainya, berjumlah 1⁄16 apabila dihitung menggunakan jumlah Abel.

Generalisasi dari 1 − 2 + 3 − 4 + ... secara umum adalah deret 1 − 2^n + 3^n − 4^n + ... dengan nilai n bilangan bulat positif. Secara matematis, deret ini mempunyai jumlah Abel sebagai berikut:[17] $${\displaystyle 1-2^{n}+3^{n}-\cdots ={\frac {2^{n+1}-1}{n+1}}B_{n+1}}$$ Di sini, B_n adalah bilangan Bernoulli. Sementara itu, apabila hanya menggunakan n bilangan genap postitif, jumlah Abel menjadi $${\displaystyle 1-2^{2k}+3^{2k}-\cdots =0,}$$ yang dapat diartikan bahwa nilai genap negatif dari fungsi zeta Riemann adalah nol. Jumlah ini dijadikan bahan ejekan oleh Niels Henrik Abel pada tahun 1826:

Deret divergen sepenuhnya merupakan pekerjaan iblis. Seseorang akan tampak bodoh jika berani menemukan bukti apa pun mengenainya. Selain itu, hasil-hasil aneh akan muncul jika ia menggunakannya. Hal-hal tersebutlah yang telah menciptakan begitu banyak ketidakbahagiaan dan begitu banyak kejanggalan. Adakah yang bisa memikirkan hal yang lebih mengerikan daripada mengatakan hal janggal seperti ini

0 = 1 − 2^2n + 3^2n − 4^2n + dst.

dengan n adalah bilangan positif. Ini adalah sesuatu yang bisa dijadikan bahan lelucon, Teman-teman.[18]

Guru Cesàro, Eugène Charles Catalan, juga meremehkan deret divergen. Oleh karena itu, di bawah pengaruh Catalan, Cesàro awalnya menyebut "rumus konvensional" untuk 1 − 2^n + 3^n − 4^n + ... sebagai "persamaan yang tidak masuk akal". Hal tersebut tampak pada tahun 1883 ketika Cesàro mengungkapkan bahwa rumus tersebut secara matematis salah, tetapi memiliki beberapa manfaat. Pada akhirnya, dalam Sur la multiplication des séries tahun 1890, Cesàro mengubah pikirannya dan mengambil pendekatan yang lebih terbuka. Pendekatan ini ia mulai dengan pendefinisian ulang.[19]

Deret umum tersebut juga dipelajari untuk nilai nonbilangan bulat n, pembentuk fungsi eta Dirichlet. Salah satu tujuan Euler mempelajari hal tersebut adalah karena hubungannya dengan persamaan fungsional fungsi eta. Euler sendiri telah menjadi terkenal karena menemukan nilai fungsi zeta pada bilangan bulat genap positif (termasuk masalah Basel). Selain itu, ia juga telah mencoba menemukan nilai fungsi zeta pada bilangan bulat ganjil positif (termasuk konstanta Apéry). Akan tetapi, tidak ada solusi yang tepat untuk masalah tersebut dan masih sulit dipahami hingga saat ini. Untuk melanjutkan, ketika hubungan tersebut ditemukan, hasil dari fungsi eta akan mengarah langsung pada persamaan fungsional fungsi zeta Riemann. Dalam menemukan hasil yang dimaksud, Euler menggunakan metodenya sendiri (metode Euler) karena nilai deret Dirichlet fungsi tersebut dapat ditentukan oleh jumlah Abel di titik mana pun. Sementara itu, apabila metodenya Euler diterapkan pada fungsi zeta, penentuan nilainya dengan penjumlahan Abel akan jauh lebih sulit jika dijumlahkan pada titik divergensi.[20] Hal ini terjadi karena sebagian besar deret pembentuk fungsi zeta membutuhkan metode penjumlahan yang lebih baik. Salah satu contohnya adalah deret terkenal 1 + 2 + 3 + 4 + ⋯, pasangan 1 − 2 + 3 − 4 + .... Di luar matematika, deret tersebut memiliki penerapan yang luas pada ilmu fisika.

Lihat juga

• 1 + 2 + 3 + 4 + ⋯
• 1 + 1 + 1 + 1 + ⋯
• 1 + 2 + 4 + 8 + ⋯

Referensi

1. Hardy 1949, hlm. 8.
2. Beals 2004, hlm. 23.
3. Hardy 1949, hlm. 6 menyajikan penurunan ini bersamaan dengan evaluasi deret Grandi 1 − 1 + 1 − 1 + ....
4. Hardy 1949, hlm. 6.
5. Ferraro 1999, hlm. 130.
6. Hardy 1949, hlm. 3; Weidlich 1950, hlm. 52–55.
7. Alabdulmohsin 2018.
8. Hardy 1949, hlm. 9. Untuk detail perhitungan selengkapnya, lihat Weidlich 1950, hlm. 17–18.
9. Ferraro 1999, hlm. 118; Tucciarone 1973, hlm. 10. Ferraro mengkritik penjelasan Tucciarone (p. 7) tentang bagaimana Hölder sendiri memikirkan hasil umum, tetapi penjelasan kedua penulis mengenai perlakuan Hölder terhadap 1 − 2 + 3 − 4 + ... serupa.
10. Ferraro 1999, hlm. 123–128.
11. Euler, Willis & Osler 2006, hlm. 2. Meskipun makalah tersebut ditulis pada tahun 1749, namun baru diterbitkan pada tahun 1768.
12. Euler, Willis & Osler 2006, hlm. 3, 25.
13. Misalnya, Lavine 1994, hlm. 23 mendukung perpecahan yang panjang tetapi tidak melaksanakannya; Vretblad 2003, hlm. 231 menghitung produk Cauchy. Nasihat Euler tidak jelas; lihat Euler, Willis & Osler 2006, hlm. 3, 26. John Baez [en] bahkan menyarankan metode teori kategori yang melibatkan himpunan lonjong perkalian dan osilator harmonis kuantum. Baez, John C. Euler's Proof That 1 + 2 + 3 + ... = −1/12 (PDF). Diarsipkan 2017-10-13 di Wayback Machine. math.ucr.edu (19 Desember 2003). Diakses pada 11 Maret 2007.
14. Shawyer & Watson 1994, hlm. 32.
15. Saichev & Woyczyński 1996, hlm. 260–264.
16. Kline 1983, hlm. 313.
17. Hardy 1949, hlm. 3; Knopp 1990, hlm. 491.
18. Grattan-Guinness 1970, hlm. 80. Lihat Markusevič 1967, hlm. 48, untuk terjemahan berbeda dari bahasa Prancis asli; nadanya tetap sama.
19. Ferraro 1999, hlm. 120–128.
20. Euler, Willis & Osler 2006, hlm. 20–25.

Daftar pustaka

• Alabdulmohsin, Ibrahim M. (2018). "Analytic summability theory". Summability Calculus. Springer International Publishing. hlm. 65–91. doi:10.1007/978-3-319-74648-7_4. ISBN 978-3-319-74647-0. 
• Beals, Richard (2004). Analysis: An Introduction. Cambridge UP. ISBN 978-0-521-60047-7. 
• Davis, Harry F. (Mei 1989). Fourier Series and Orthogonal Functions. Dover. ISBN 978-0-486-65973-2. 
• Euler, Leonhard; Willis, Lucas; Osler, Thomas J. (2006). "Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series". The Euler Archive. Diakses tanggal 2007-03-22.  Originally published as Euler, Leonhard (1768). "Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques". Mémoires de l'Académie des Sciences de Berlin. 17: 83–106. 
• Ferraro, Giovanni (Juni 1999). "The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics". Archive for History of Exact Sciences. 54 (2): 101–135. doi:10.1007/s004070050036.  Parameter |s2cid= yang tidak diketahui akan diabaikan (bantuan)
• Grattan-Guinness, Ivor (1970). The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press. ISBN 978-0-262-07034-8. 
• Hardy, G. H. (1949). Divergent Series. Clarendon Press. xvi+396. ISBN 978-0-8218-2649-2. LCCN 49005496. MR 0030620. OCLC 808787.  2nd Ed. published by Chelsea Pub. Co., 1991. LCCN 91-75377. ISBN 0-8284-0334-1.
• Kline, Morris (November 1983). "Euler and Infinite Series". Mathematics Magazine. 56 (5): 307–314. CiteSeerX 10.1.1.639.6923 . doi:10.2307/2690371. JSTOR 2690371. 
• Knopp, Konrad (1990). Theory and Application of Infinite Series. New York: Dover Publications. ISBN 0486661652. LCCN 89071388. 
• Lavine, Shaughan (1994). Understanding the Infinite. Harvard UP. ISBN 978-0-674-92096-5. 
• Markusevič, Aleksej Ivanovič (1967). Series: fundamental concepts with historical exposition (edisi ke-English translation of 3rd revised edition (1961) in Russian). Delhi, India: Hindustan Pub. Corp. hlm. 176. LCCN sa68017528. OCLC 729238507.  Author also known as A. I. Markushevich and Alekseï Ivanovitch Markouchevitch. Also published in Boston, Mass by Heath with OCLC 474456247. Additionally, OCLC 208730, OCLC 487226828.
• Saichev, A. I.; Woyczyński, W. A. (1996). Distributions in the Physical and Engineering Sciences, Volume 1. Birkhaüser. ISBN 978-0-8176-3924-2. 
• Shawyer, Bruce; Watson, Bruce (1994). Borel's Methods of Summability: Theory and Application. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York. ISBN 0-19-853585-6. MR 1320266. 
• Tucciarone, John (Januari 1973). "The development of the theory of summable divergent series from 1880 to 1925". Archive for History of Exact Sciences. 10 (1–2): 1–40. doi:10.1007/BF00343405.  Parameter |s2cid= yang tidak diketahui akan diabaikan (bantuan)
• Vretblad, Anders (2003). Fourier Analysis and Its Applications. Springer. ISBN 978-0-387-00836-3. 
• Weidlich, John E. (Juni 1950). Summability methods for divergent series. Stanford M.S. theses. OCLC 38624384.