在抽象幾何學 中,立方體半形 是一種僅由一半數量的立方體 面構成的抽象多面體。這個抽象多面體與立方體類似,它們的每個頂點都是3個正方形的公共頂點,然而立方體有6個面,而立方體半形僅有3個面;同時,這個立體無法嵌入在三維歐幾里得空間中[ 2] 正四面體 的皮特里對偶 [ 3]
立方體半形由3個面 、6條邊 和4個頂點 組成,每個面都是正方形 ,且每個頂點都是3個正方形的公共頂點,在施萊夫利符號中可以用{4,3}/2或{4,3}3 來表示,其中{4,3}代表且每個頂點都是3個正方形的公共頂點[ 4] 正六面體 ,因此用「/2」 符號來表示所有元素都僅有立方體的一半數量[ 5] [ 6]
立方體半形的對偶多面體為正八面體半形 ,這個在更高維度的類比結構中同樣成立,即
n
+
1
{\displaystyle n+1}
施萊夫利符號 :
{
4
,
3
n
−
1
}
n
+
1
{\displaystyle {\left\{4,3^{n-1}\right\}}_{n+1}}
n
+
1
{\displaystyle n+1}
{
3
n
−
1
,
4
}
n
+
1
{\displaystyle {\left\{3^{n-1},4\right\}}_{n+1}}
[ 5] [ 6]
特別地,這個立體的每個面皆與相鄰面共用2條邊,且每個面都包含了立體中所有頂點。一般而言,多胞形的面可以透過其點集來決定[ 7]
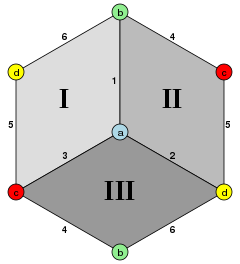
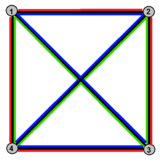
立方體半形可從有公共頂點的半個立方體(即三個面,下圖的I、II、III)開始構造。此形狀的邊界為一個六邊形,然後下一步是將此六條邊分成三組對邊(下圖的4、5、6),將每對邊(沿同一方向,例如順時針)黏合,就得到立方體半形[ 4] [ 8] [ 4] K 4 完全圖 嵌入於射影平面 上的結果。[ 4]
立方體半形可被視為是射影多面體 四邊形 構成的實射影平面 鑲嵌 )[ 9] 對蹠點 ,同時確保連接的部分能將半球體平均分割成三等份。
立方體半形和半立方體 不同,立方體半形是一個射影多面體 [ 2] 半形 可以視為立方體的商空間 ,而半 立方體則不是,半立方體只有頂點為立方體頂點的子集 。
皮特里四面體是正四面體 的皮特里對偶 [ 1] [ 10] [ 4] 正四面體 ,這意味著其皮特里多邊形可以與半立方體 (此例對應正四面體 )的面對應[ 11] 皮特里對偶 。[ 1] [ 10]
皮特里四面體由3個面、6條邊和4個頂點組成,其中,3個面皆為正四面體 的皮特里多邊形 。正四面體 的皮特里多邊形 是一個扭歪四邊形。[ 12] [ 13] [ 14]
皮特里四面體是一個不可定向且歐拉示性數為1的幾何結構[ 1]
皮特里四面體的頂點、邊和面數皆為立方體的一半,因此皮特里四面體可以被立方體(的表面)二重覆蓋 [ 1] 八面體半形 [ 1] 截半 為截半立方體半形 [ 1] [ 15]
立方體半形是正多面體的半形體之一,其他也是正多面體的半形之結構有[ 6]
立方體半形與皮特里四面體拓樸同構,其可以視為是正多面體的皮特里對偶之一。其他也是正多面體的皮特里對偶之幾何結構有:[ 16]
^ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 The hemicube . Regular Map database - map details. [2021-07-24 ] . (原始内容 存档于2019-05-02). ^ 2.0 2.1 Mark Mixer. Introduction to abstract polytopes (PDF) . Northeastern University. 2009-05-19 [2021-07-31 ] . (原始内容 (PDF) 存档于2021-08-06). ^ Pellicer, D, Gráficas cpr y polytopos abstractos regulares (PDF) , Universidad Nacional Autónoma de México, Mexico City, Mexico, 2007 [2021-07-31 ] , (原始内容 (PDF) 存档于2021-08-06) ^ 4.0 4.1 4.2 4.3 4.4 Séquin, Carlo H and Lanier, Jaron. Hyperseeing the regular Hendecachoron . Proc ISAMA. 2007: 159–166 [2021-08-04 ] . (原始内容 存档于2021-08-04). ^ 5.0 5.1 Hartley, Michael I. The Classification of Rank 4 Locally Projective Polytopes and Their Quotients (PDF) . arXiv preprint math/0310429. 2003 [2021-07-31 ] . (原始内容 (PDF) 存档于2021-08-06). ^ 6.0 6.1 6.2 McMullen, Peter; Schulte, Egon, 6C. Projective Regular Polytopes, Abstract Regular Polytopes 1st, Cambridge University Press: 162–165 , December 2002, ISBN 0-521-81496-0 ^ Kaibel, Volker and Pfetsch, Marc E. Computing the face lattice of a polytope from its vertex-facet incidences (PDF) . Computational Geometry (Elsevier). 2002, 23 (3): 281–290 [2021-07-31 ] . (原始内容 (PDF) 存档于2021-08-06). ^ Carlo H. Séquin. Sculpture designs and math models . University of California, Berkeley. [2021-07-31 ] . (原始内容 存档于2021-10-22). "Ribbed Hemicube" (June 2007) - 5" ^ Helfand, Ilanit, Constructions of k-orbit Abstract Polytopes, Northeastern University, 2013 ^ 10.0 10.1 The tetrahedron . Regular Map database - map details. [2021-07-24 ] . (原始内容 存档于2021-08-23). ^ Bracho, Javier and Hubard, Isabel and Pellicer, Daniel. A Finite Chiral 4-Polytope in
R
4
{\displaystyle \mathbb {R} ^{4}}
52 (4): 799––805. ^ Gorini, Catherine A., Geometry at Work , MAA Notes 53 , Cambridge University Press: 181, 2000, ISBN 9780883851647 ^ McMullen, Peter; Schulte, Egon, Abstract Regular Polytopes , Encyclopedia of Mathematics and its Applications 92 , Cambridge University Press: 192, 2002, ISBN 9780521814966 ^ Barnard, L., Aro -- Healing Touching Lives -- Theories, Techniques and Therapies: The Techniques and Therapies of Aro-Healing , Xlibris UK, 2014 [2021-07-31 ] , ISBN 9781483631646原始内容 存档于2021-07-31) ^ Hemi-cuboctahedron . Regular Map database - map details. [2021-07-24 ] . (原始内容 存档于2021-01-26). ^ Regular maps in the orientable surface of genus 0 . Regular Map database - map details. [2021-07-31 ] . (原始内容 存档于2021-10-19).