扭稜小星形十二面體

扭稜小星形十二面體

類別	均勻星形多面體
對偶多面體	中五角六十面体（英语：Medial pentagonal hexecontahedron）
識別
名稱	扭稜小星形十二面體 Snub dodecadodecahedron
參考索引	U40, C49, W111
鮑爾斯縮寫 （verse-and-dimensions的wikia：Bowers acronym）	siddid
數學表示法
考克斯特符號 （英语：Coxeter-Dynkin diagram）	[1]
施萊夫利符號	sr{5⁄2,5}
威佐夫符號 （英语：Wythoff symbol）	| 2 5⁄2 5[2][3]
性質
面	84
邊	150
頂點	60
歐拉特徵數	F=84, E=150, V=60 （χ=-6）
組成與佈局
面的種類	20個正三角形 12個正五邊形 12個正五角星
頂點圖	3.3.5⁄2.3.5
對稱性
對稱群	Ih, [5,3]^+, 532
圖像
3.3.5⁄2.3.5 （頂點圖） 中五角六十面体（英语：Medial pentagonal hexecontahedron） （對偶多面體）
查 论 编

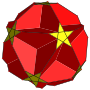
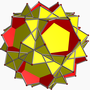
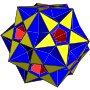
在幾何學中，扭稜小星形十二面體是一種星形均勻多面體，索引為U₄₀，由60個三角形面、12個正五邊形面和12個正五角星面組成[4][5]，且有12組正五邊形面和正五角星面互相平行[6]:174，為小星形十二面體經扭棱變換後的結果，具有二十面體群對稱性[4][7][8][3]。 扭稜小星形十二面體的對偶多面體為中五角六十面体（英语：Medial pentagonal hexecontahedron）[2]，並與反扭稜小星形十二面體拓樸同構[9]。

性質

扭稜小星形十二面體一共有84個面、150條邊和60個頂點[3]。在其84個面中，有60個正三角形面、12個正五邊形面和12個五角星面[4][5]，換句話說，具有3條邊的面共60個且具有5條邊的面共24個[10]。其12個正五邊形面和12個五角星面中，有12組正五邊形面和五角星面互相平行，這與截半大十二面體非常類似。[6]:174其60個頂點每個頂點都是1個十角星、1個五角星和3個三角形的公共頂點，並且這些面在頂都周圍皆是依照五角星、三角形、五邊形、三角形、三角形和三角形的順序排列，在頂點圖中可以用(5⁄2,3,5,3,3)[11]或(3.3.5⁄2.3.5)[4]來表示。

表示法

扭稜小星形十二面體在考克斯特—迪肯符号（英语：Coxeter-Dynkin diagram）中可以表示為（s5⁄2s5s）[1]，在施莱夫利符号中可以表示為sr{5⁄2,5}，在威佐夫記號中可以表示為| 2 5⁄2 5。[2][3][12][13][4][10][5]

尺寸

若扭稜小星形十二面體的邊常為單位長，則其外接球半徑為多項式${\displaystyle 64x^{4}-192x^{3}+180x^{2}-65x+8}$之較大正實根（約為1.6242）的平方根[8]，約為1.27443994[14]：

${\displaystyle {\sqrt {\operatorname {root} \left(64x^{4}-192x^{3}+180x^{2}-65x+8\right)}}\approx 1.27443988203802179}$[8]

中分球半徑則為多項式${\displaystyle 256x^{4}-512x^{3}+240x^{2}-28x+1}$之正實根的平方根[8]：

${\displaystyle {\sqrt {\operatorname {root} \left(256x^{4}-512x^{3}+240x^{2}-28x+1\right)}}\approx 1.172261495114928}$

頂點座標

扭稜小星形十二面體的頂點座標為下列座標的偶置換：[8]

(±2α, ±2, ±2β),

(±(α+β/τ+τ), ±(-ατ+β+1/τ), ±(α/τ+βτ-1))、

(±(-α/τ+βτ+1), ±(-α+β/τ-τ), ±(ατ+β-1/τ))、

(±(-α/τ+βτ-1), ±(α-β/τ-τ), ±(ατ+β+1/τ)) 與

(±(α+β/τ-τ), ±(ατ-β+1/τ), ±(α/τ+βτ+1))，

帶有偶數個正號，其中

β = (α^2/τ+τ)/(ατ−1/τ)，

當中的 τ = (1+√5)/2為黃金比例且 α是多項式τα^4−α^3+2α^2−α−1/τ的正實根，約為0.7964421。 若上述座標使用奇置換並帶有奇數個正號的話，則會得到扭稜小星形十二面體的另一種形式，即另一種形式的對映體。

參見

• 均勻多面體列表（英语：List_of_uniform_polyhedra）
• 反扭稜小星形十二面體

參考文獻

1. Richard Klitzing. Icosahedral Symmetries uniform polyhedra, Polytopes & their Incidence Matrices. bendwavy.org. [2022-08-07]. （原始内容存档于2018-07-07）. 
2. Weisstein, Eric W. (编). Snub Dodecadodecahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
3. Roman E. Maeder. 40: snub dodecadodecahedron. mathconsult.ch. [2022-08-14]. （原始内容存档于2022-08-14）. 
4. Zvi Har'El. Kaleido Data: Uniform Polyhedron #45, snub dodecadodecahedron. harel.org.il. 2006-11-14 [2022-08-14]. （原始内容存档于2022-08-14）. 
5. Robert Whittaker. The Snub Dodecadodecahedron. polyhedra.mathmos.net. [2022-08-14]. （原始内容存档于2021-09-22）. 
6. Wenninger, M.J. Polyhedron Models. Cambridge University Press. 1974 [2021-09-05]. ISBN 9780521098595. LCCN 69010200. （原始内容存档于2021-08-31）. 
7. Paul Bourke. Uniform Polyhedra (80). 2004-10 [2022-08-14]. （原始内容存档于2014-04-02）. 
8. David I. McCooey. Self-Intersecting Snub Quasi-Regular Polyhedra: Snub Dodecadodecahedron. [2022-08-14]. （原始内容存档于2022-02-14）. 
9. Richard Klitzing. siddid, snub dodecadodecahedron. bendwavy.org. [2022-08-14]. （原始内容存档于2022-08-17）. 
10. V.Bulatov. snub dodecadodecahedron. [2022-08-14]. （原始内容存档于2021-02-28）. 
11. Jim McNeill. Augmenting the snub dodecadodecahedron. orchidpalms.com. [2022-08-14]. （原始内容存档于2016-03-06）. 
12. George W. Hart. Uniform Polyhedra --- List. 1996 [2022-08-14]. （原始内容存档于2018-09-19）. 
13. Adrian Rossiter. snub dodecadodecahedron. antiprism.com. [2022-08-14]. （原始内容存档于2022-08-14）. 
14. Eric W. Weisstein. Snub Dodecadodecahedron. archive.lib.msu.edu. 1999-05-26 [2022-08-14]. （原始内容存档于2021-12-07）.