循环神经网络

提示：此条目的主题不是结构递归神经网络。

循环神经网络（Recurrent neural network：RNN）是神經網絡的一種。单纯的RNN因为无法处理随着递归，权重指数级爆炸或梯度消失问题，难以捕捉长期时间关联；而结合不同的LSTM可以很好解决这个问题。[1][2]

时间循环神经网络可以描述动态时间行为，因为和前馈神经网络（feedforward neural network）接受较特定结构的输入不同，RNN将状态在自身网络中循环传递，因此可以接受更广泛的时间序列结构输入。手写识别是最早成功利用RNN的研究结果。[3]

历史

递归神经网络是基于大卫·鲁梅尔哈特1986年的工作[4]。1982年，约翰·霍普菲尔德发现了Hopfield神经网络——一种特殊的RNN。1993年，一个神经历史压缩器系统解决了一个“非常深度学习”的任务，这个任务在RNN展开之后有1000多个后续层[5]。

LSTM

Hochreiter和Schmidhuber于1997年提出了长短期记忆(LSTM)网络，并在多个应用领域创造了精确度记录[6]。

大约在2007年，LSTM开始革新语音识别领域，在某些语音应用中胜过传统模型[7]。2009年，一个由 CTC（英语：Connectionist temporal classification） 训练的LSTM网络赢得了多项连笔手写识别竞赛，成为第一个赢得模式识别竞赛的RNN。[8][9]2014年，百度在不使用任何传统语音处理方法的情况下，使用经过CTC训练的RNNs打破了Switchboard Hub5'00 语音识别基准。[10]

LSTM还改进了大词汇量语音识别[11][12]和文本到语音合成[13]并在谷歌安卓系统中使用[8][14]。据报道，2015年，谷歌语音识别通过接受过CTC训练的LSTM(谷歌语音搜索使用的)实现了49%的引用量的大幅提升。[15]

LSTM打破了改进机器翻译[16]、语言建模[17]和多语言处理的记录[18]。 LSTM 结合卷积神经网络改进了图像自动标注 。[19]

循环神经网络

编码器

循环神经网络将输入序列${\displaystyle {\vec {x}}}$编码为一个固定长度的隐藏状态${\displaystyle {\vec {h}}}$，这里有（用自然语言处理作为例子）：

• ${\displaystyle {\vec {x}}=(x_{t},...,x_{1})}$ 是输入序列，比如编码为数字的一系列词语，整个序列就是完整的句子。
• ${\displaystyle {\vec {h_{t}}}=f(x_{t},{\vec {h_{t-1}}})}$是随时间更新的隐藏状态。当新的词语输入到方程中，之前的状态${\displaystyle {\vec {h_{t-1}}}}$就转换为和当前输入${\displaystyle x_{t}}$相关的${\displaystyle {\vec {h_{t}}}}$，距离当前时间越长，越早输入的序列，在更新后的状态中所占权重越小，从而表现出时间相关性。[20]

其中，计算隐藏状态的方程${\displaystyle f(x,h)}$是一个非线性方程，可以是简单的Logistic方程（tanh），也可以是复杂的LSTM单元（Long Short-Term Memory）。[20] [21] 而有了隐藏状态序列，就可以对下一个出现的词语进行预测：

• ${\displaystyle p(y_{t})=p(y_{t}\,|\,y_{t-1},...,y_{1})}$，其中${\displaystyle y_{t}}$是第t个位置上的输出，它的概率基于之前输出的所有词语。
• 以上概率可以通过隐藏状态来计算：${\displaystyle p(y_{t})=g(y_{t-1},{\vec {h_{t}}},{\vec {c}})}$，${\displaystyle {\vec {c}}}$是所有隐藏状态的编码，总含了所有隐藏状态，比如可以是简单的最终隐藏状态${\displaystyle {\vec {h_{t}}}}$，也可以是非线性方程的输出${\displaystyle f(h_{t},...,h_{1})}$。因为隐藏状态t就编码了第t个输入前全部的输入信息，${\displaystyle y_{t}}$也迭代式地隐含了之前的全部输出信息，所以这个概率计算方法是合理的。

这里的非线性方程${\displaystyle g(y,h,c)}$可以是一个复杂的前馈神经网络，也可以是简单的非线性方程（但有可能因此无法适应复杂的条件而得不到任何有用结果）。给出的概率可以用监督学习的方法优化内部参数来给出翻译，也可以训练后用来给可能的备选词语，用计算其第j个备选词${\displaystyle y_{t,j}}$出现在下一位置的概率，给它们排序。排序后用于其它翻译系统，可以提升翻译质量。

解码器

更复杂的情况下循环神经网络还可以结合编码器作为解码器（Decoder），用于将编码后（Encoded）的信息解码为人类可识别的信息。也就是上述例子中的${\displaystyle y_{t}=f(y_{t-1},h_{t},c)}$过程，当中非线性模型${\displaystyle f}$就是作为输出的循环神经网络。只是在解码过程中，隐藏状态因为是解码器的参数，所以为了发挥时间序列的特性，需要对${\displaystyle h_{t}'}$继续进行迭代：

• ${\displaystyle h_{t}'=g(h_{t-1},y_{t-1},c)}$，${\displaystyle {\vec {c}}}$是解码器传递给编码器的参数，是解码器中状态的summary。${\displaystyle h_{t}'}$是解码器的隐藏状态。${\displaystyle y_{t}}$是第t个输出。
• 当输入仍为${\displaystyle {\vec {x}}=(x_{t},...,x_{1})}$，输出是${\displaystyle {\vec {y}}=(y_{t},...,y_{1})}$，最大化条件概率${\displaystyle P({\vec {y}}\,|\,{\vec {x}})}$后就是最好的翻译结果。

双向读取

用两个循环神经网络双向读取一个序列可以使人工智能获得“注意力”。简单的做法是将一个句子分别从两个方向编码为两个隐藏状态，然后将两个${\displaystyle {\vec {h}}}$拼接在一起作为隐藏状态。[22] [23]这种方法能提高模型表现的原因之一可能是因为不同方向的读取在输入和输出之间创造了更多短期依赖关系，从而被RNN中的LSTM单元（及其变体）捕捉，例如在实验中发现颠倒输入序列的顺序（但不改变输出的顺序）可以意外达到提高表现的效果。[24]

架构

RNN 有很多不同的变种

完全循环

基本的 RNN 是由人工神经元（英语：Artificial neuron）组织成的连续的层的网络。给定层中的每个节点都通过有向（英语：Directed graph）(单向)连接连接到下一个连续层中的每个其他节点。每个节点(神经元)都有一个时变的实值激活。每个连接(突触)都有一个可修改的实值权重（英语：Weighting）。节点要么是输入节点(从网络外部接收数据)，要么是输出节点(产生结果)，要么是隐藏节点(在从输入到输出的过程中修改数据)。

对于离散时间设置中的监督学习，实值输入向量序列到达输入节点，一次一个向量。在任何给定的时间步长，每个非输入单元将其当前激活(结果)计算为与其连接的所有单元的激活的加权和的非线性函数。可以在特定的时间步长为某些输出单元提供主管给定的目标激活。例如，如果输入序列是对应于口语数字的语音信号，则在序列末尾的最终目标输出可以是对该数字进行分类的标签。

在强化学习环境中，没有教师提供目标信号。相反，适应度函数或奖励函数偶尔用于评估RNN的性能，它通过影响输出单元来影响其输入流，输出单元和一个可以影响环境的执行器相连。这可以被用来玩一个游戏，在这个游戏中，进度是用赢得的点数来衡量的。

每个序列产生一个误差，作为所有目标信号与网络计算的相应激活的偏差之和。对于大量序列的训练集，总误差是所有单个序列误差的总和。

Elman 网络和 Jordan 网络

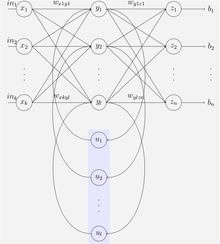
Elman 网络

Elman网络是一个三层网络(在图中水平排列为x、y和z)，添加了一组上下文单元(在图中为u)。中间(隐藏)层连接到这些权重为1的上下文单元[25]。在每个时间步，输入被向前反馈，并且学习规则被应用。固定的反向连接在上下文单元中保存隐藏单元的先前值的副本(因为它们在应用学习规则之前在连接上传播)。因此，网络可以保持某种状态，允许它执行诸如序列预测之类的任务，这些任务超出了标准多层感知器的能力。

Jordan网络类似于Elman网络。上下文单元是从输出层而不是隐藏层馈送的。Jordan网络中的上下文单元也称为状态层。他们与自己有着经常性的联系。[26]

Elman和Jordan网络也被称为“简单循环网络”。

Elman 网络[27]

${\displaystyle {\begin{aligned}h_{t}&=\sigma _{h}(W_{h}x_{t}+U_{h}h_{t-1}+b_{h})\\y_{t}&=\sigma _{y}(W_{y}h_{t}+b_{y})\end{aligned}}}$

Jordan 网络[28]

${\displaystyle {\begin{aligned}h_{t}&=\sigma _{h}(W_{h}x_{t}+U_{h}y_{t-1}+b_{h})\\y_{t}&=\sigma _{y}(W_{y}h_{t}+b_{y})\end{aligned}}}$

变量和函数

• ${\displaystyle x_{t}}$: 输入向量
• ${\displaystyle h_{t}}$: 隐藏层向量
• ${\displaystyle y_{t}}$: 输出向量
• ${\displaystyle W}$, ${\displaystyle U}$ 和 ${\displaystyle b}$: 参数矩阵和参数向量
• ${\displaystyle \sigma _{h}}$ 和 ${\displaystyle \sigma _{y}}$: 激活函数

双向循环神经网络

主条目：双向循环神经网络

双向循环神经网络（Bi-directional RNN，BRNN）基于元素的前向和后向的上下文，使用有限序列来预测或标记序列的每个元素。该方法是通过连接两个 RNN 的输出来完成的：一个从左到右处理序列，另一个从右到左处理序列。BRNN的输出是对目标信号的预测。该技术已被证明在与 LSTM RNN 结合使用时特别有用。[29][30]

参考

1. 时钟结构的RNN （页面存档备份，存于互联网档案馆），2014年2月。
2. 循环网络结构的经验之谈 （页面存档备份，存于互联网档案馆），谷歌论文，2015年。
3. A. Graves, M. Liwicki, S. Fernandez, R. Bertolami, H. Bunke, J. Schmidhuber. A Novel Connectionist System for Improved Unconstrained Handwriting Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 5, 2009.
4. Williams, Ronald J.; Hinton, Geoffrey E.; Rumelhart, David E. Learning representations by back-propagating errors. Nature. October 1986, 323 (6088): 533–536. Bibcode:1986Natur.323..533R. ISSN 1476-4687. doi:10.1038/323533a0. 
5. Schmidhuber, Jürgen. Habilitation thesis: System modeling and optimization (PDF). 1993. ^[失效連結] Page 150 ff demonstrates credit assignment across the equivalent of 1,200 layers in an unfolded RNN.
6. Hochreiter, Sepp; Schmidhuber, Jürgen. Long Short-Term Memory. Neural Computation. 1997-11-01, 9 (8): 1735–1780. PMID 9377276. doi:10.1162/neco.1997.9.8.1735. 
7. Fernández, Santiago; Graves, Alex; Schmidhuber, Jürgen. An Application of Recurrent Neural Networks to Discriminative Keyword Spotting. ICANN'07. Berlin, Heidelberg: Springer-Verlag. 2007: 220–229 [2020-02-27]. ISBN 978-3-540-74693-5. （原始内容存档于2018-10-06）.  |journal=被忽略 (帮助)
8. 引用错误：没有为名为schmidhuber2015的参考文献提供内容
9. Graves, Alex; Schmidhuber, Jürgen. Bengio, Yoshua; Schuurmans, Dale; Lafferty, John; Williams, Chris editor-K. I.; Culotta, Aron , 编. Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks. Neural Information Processing Systems (NIPS) Foundation: 545–552. 2009 [2020-02-27]. （原始内容存档于2020-09-07）. 
10. Hannun, Awni; Case, Carl; Casper, Jared; Catanzaro, Bryan; Diamos, Greg; Elsen, Erich; Prenger, Ryan; Satheesh, Sanjeev; Sengupta, Shubho. Deep Speech: Scaling up end-to-end speech recognition. 2014-12-17. arXiv:1412.5567  [cs.CL]. 
11. Sak, Haşim; Senior, Andrew; Beaufays, Françoise. Long Short-Term Memory recurrent neural network architectures for large scale acoustic modeling (PDF). 2014 [2020-02-28]. （原始内容 (PDF)存档于2019-09-22）. 
12. Li, Xiangang; Wu, Xihong. Constructing Long Short-Term Memory based Deep Recurrent Neural Networks for Large Vocabulary Speech Recognition. 2014-10-15. arXiv:1410.4281  [cs.CL]. 
13. Fan, Bo; Wang, Lijuan; Soong, Frank K.; Xie, Lei (2015) "Photo-Real Talking Head with Deep Bidirectional LSTM", in Proceedings of ICASSP 2015
14. Zen, Heiga; Sak, Haşim. Unidirectional Long Short-Term Memory Recurrent Neural Network with Recurrent Output Layer for Low-Latency Speech Synthesis (PDF). Google.com. ICASSP: 4470–4474. 2015 [2020-02-27]. （原始内容存档 (PDF)于2021-05-09）. 
15. Sak, Haşim; Senior, Andrew; Rao, Kanishka; Beaufays, Françoise; Schalkwyk, Johan. Google voice search: faster and more accurate. September 2015 [2020-02-27]. （原始内容存档于2016-03-09）. 
16. Sutskever, Ilya; Vinyals, Oriol; Le, Quoc V. Sequence to Sequence Learning with Neural Networks (PDF). Electronic Proceedings of the Neural Information Processing Systems Conference. 2014, 27: 5346 [2020-02-27]. Bibcode:2014arXiv1409.3215S. arXiv:1409.3215 . （原始内容存档 (PDF)于2021-05-09）. 
17. Jozefowicz, Rafal; Vinyals, Oriol; Schuster, Mike; Shazeer, Noam; Wu, Yonghui. Exploring the Limits of Language Modeling. 2016-02-07. arXiv:1602.02410  [cs.CL]. 
18. Gillick, Dan; Brunk, Cliff; Vinyals, Oriol; Subramanya, Amarnag. Multilingual Language Processing From Bytes. 2015-11-30. arXiv:1512.00103  [cs.CL]. 
19. Vinyals, Oriol; Toshev, Alexander; Bengio, Samy; Erhan, Dumitru. Show and Tell: A Neural Image Caption Generator. 2014-11-17. arXiv:1411.4555  [cs.CV]. 
20. Cho, K., van et al (2014a). 统计机器翻译方法：使用RNN进行短语编码解码。. [2015-04-23]. （原始内容存档于2022-02-08）. 
21. 经典模型Long Short-Term Memory的原论文，发表于1997年。. [2015-04-23]. （原始内容存档于2019-08-09）. 
22. Bidirectional RNN, (1997)
23. Cho. k. et al 使用RNN和对齐模型的短语统计机器翻译方法。(2014.a.). [2015-04-23]. （原始内容存档于2022-06-19）. 
24. 神经网络学习：序列到序列 （页面存档备份，存于互联网档案馆），作者Sutskever，2014年。
25. Cruse, Holk; Neural Networks as Cybernetic Systems （页面存档备份，存于互联网档案馆）, 2nd and revised edition
26. 引用错误：没有为名为bmm6152的参考文献提供内容
27. Elman, Jeffrey L. Finding Structure in Time. Cognitive Science. 1990, 14 (2): 179–211. doi:10.1016/0364-0213(90)90002-E. 
28. Jordan, Michael I. Serial Order: A Parallel Distributed Processing Approach. Neural-Network Models of Cognition 121. 1997-01-01: 471–495. ISBN 9780444819314. doi:10.1016/s0166-4115(97)80111-2.  |journal=被忽略 (帮助)
29. Graves, Alex; Schmidhuber, Jürgen. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Networks. IJCNN 2005. 2005-07-01, 18 (5): 602–610. CiteSeerX 10.1.1.331.5800 . PMID 16112549. doi:10.1016/j.neunet.2005.06.042. 
30. Thireou, Trias; Reczko, Martin. Bidirectional Long Short-Term Memory Networks for Predicting the Subcellular Localization of Eukaryotic Proteins. IEEE/ACM Transactions on Computational Biology and Bioinformatics. July 2007, 4 (3): 441–446. PMID 17666763. S2CID 11787259. doi:10.1109/tcbb.2007.1015. 

外部連結

• A Critical Review of Recurrent Neural Networks for Sequence Learning （页面存档备份，存于互联网档案馆）