史密斯-沃特曼算法

史密斯-沃特曼算法步骤的动态示意图（详细步骤见这里）

史密斯-沃特曼算法（Smith-Waterman algorithm）是一种进行局部序列比对（相对于全局比对）的算法，用于找出两个核苷酸序列或蛋白质序列之间的相似区域。该算法的目的不是进行全序列的比对，而是找出两个序列中具有高相似度的片段。

该算法由坦普尔·史密斯和迈克尔·沃特曼于1981年提出[1]。史密斯-沃特曼算法是尼德曼-翁施算法的一个变体，二者都是动态规划算法。这一算法的优势在于可以在给定的打分方法下找出两个序列的最优的局部比对（打分方法使用了置换矩阵和空位罚分）。该算法和尼德曼-翁施算法的主要区别在于该算法不存在负分（负分被替换为零），因此局部比对成为可能。回溯从分数最高的矩阵元素开始，直到遇到分数为零的元素停止。分数最高的局部比对结果在此过程中产生。在实际运用中，人们通常使用该算法的优化版本[2][3][4]。

历史

生物学上一个基本问题是，一个基因或者蛋白是否和别的基因或者蛋白存在联系。蛋白质在序列层次的关联暗示了其同源性，同时暗示了它们可能有类似的功能。通过分析多个DNA或者蛋白质序列，我们可能会发现一些保守序列和区域。这种基因序列或者蛋白质序列之间关联性的分析就是通过序列比对来完成的。如今，人们完成了许多不同生物体的基因组分析，获得了大量的基因和蛋白质序列数据。序列比对能够向我们揭示某一生物体中蛋白质之间的关联以及蛋白质在不同生物体中的关联，从而进一步理解生命和进化。

序列比对起源于1970年。Saul B. Needleman和Christian D. Wunsch于1970提出了一个启发式的同源算法[5]，称为尼德曼-翁施算法。该算法使用迭代的方法计算出一个矩阵，从而达到全局比对的效果。一些其他的启发式分析方法也在70年代被提出。Sankoff[6]，Reichert[7]，Beyer[8]等人提出了一些严谨的数学的算法用来分析序列。然而这些方法通常难以揭示序列的生物学意义。 Sellers提出了一套测量序列距离的方法[9]。沃特曼等于1976年在该方法的基础上，增加了插入和删除任意长度片段的方法[10]。该方法解决了如何用最小的基因突变的次数将一个序列转变成另一个序列的问题。之后，坦普尔·史密斯和迈克尔·沃特曼于1981年提出了史密斯-沃特曼算法，解决了局部比对问题。

算法

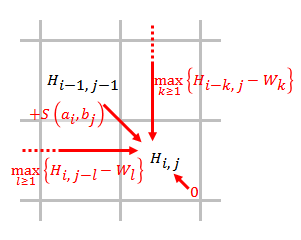
史密斯-沃特曼算法打分方法示意图

设要比对的两序列为${\displaystyle A=a_{1}a_{2}...a_{n}}$和${\displaystyle B=b_{1}b_{2}...b_{m}}$，其中${\displaystyle n}$和${\displaystyle m}$分别为序列${\displaystyle A}$和${\displaystyle B}$的长度。

1. 确定置换矩阵和空位罚分方法
   • ${\displaystyle s(a,b)}$ - 组成序列的元素之间的相似性得分
   • ${\displaystyle W_{k}}$ - 长度为${\displaystyle k}$的空位罚分
2. 建立得分矩阵${\displaystyle H}$并初始化其首行和首列。该矩阵的大小为${\displaystyle n+1}$行${\displaystyle m+1}$列（注意计数从0开始）。

   ${\displaystyle H_{k0}=H_{0l}=0,(0\leq k\leq n,0\leq l\leq m)}$

3. 从左到右，从上到下进行打分，填充得分矩阵${\displaystyle H}$剩余部分

   ${\displaystyle H_{ij}=\max {\begin{cases}H_{i-1,j-1}+s(a_{i},b_{j}),\\\max _{k\geq 1}\{H_{i-k,j}-W_{k}\},\\\max _{l\geq 1}\{H_{i,j-l}-W_{l}\},\\0\end{cases}}\qquad (1\leq i\leq n,1\leq j\leq m)}$

   其中，

   ${\displaystyle H_{i-1,j-1}+s(a_{i},b_{j})}$表示将${\displaystyle a_{i}}$和${\displaystyle b_{j}}$比对的相似性得分，

   ${\displaystyle H_{i-k,j}-W_{k}}$表示${\displaystyle a_{i}}$位于一段长度为${\displaystyle k}$的删除的末端的得分，

   ${\displaystyle H_{i,j-l}-W_{l}}$表示${\displaystyle b_{j}}$位于一段长度为${\displaystyle l}$的删除的末端的得分，

   ${\displaystyle 0}$表示${\displaystyle a_{i}}$和${\displaystyle b_{j}}$到此为止无相似性。

4. 回溯。从矩阵${\displaystyle H}$中得分最高的元素开始根据得分的来源回溯至上一位置，如此反复直至遇到得分为${\displaystyle 0}$的元素。

解释

史密斯-沃特曼算法通过字母的匹配，删除和插入操作，把两条序列进行排列。实际上插入和删除都是引入空位的操作（在不同序列上）。序列1上某一位置的插入相当于在序列2上对应位置的删除。在实际计算中，只需要考虑何时引入空位即可。

该算法主要分两步，计算得分矩阵和寻找最优比对序列。可以简单描述为：

1. 确定置换矩阵及空位罚分方法。置换矩阵赋予每一碱基对或残基对匹配或错配的分数，相同或类似则赋予正值，不同或不相似赋予0分或者负分。空位罚分决定了引入或延长空位的分值。研究者应当根据比对的目的选择合适的置换矩阵及空位罚分。另外通过比较不同的置换矩阵及空位罚分的组合所带来的比对结果也可以帮助研究者进行选择。
2. 初始化得分矩阵。得分矩阵的长度和宽度分别为两序列的长度+1。其首行和首列所有元素均设为0。额外的首行和首列得以让一序列从另一序列的任意位置开始进行比对，分值为零使其不受罚分。
3. 打分。对得分矩阵的每一元素进行从左到右、从上到下的打分，考虑匹配或错配（对角线得分），引入空位（水平或垂直得分）分别带来的结果，取最高值作为该元素的分值。如果分值低于0，则该元素分值为0。打分的同时记录下每一个分数的来源用来回溯。
4. 回溯。通过动态规划的方法，从得分矩阵的最大分值的元素开始回溯直至分数为0的元素。具有局部最高相似性的片段在此过程中产生。具有第二高相似性的片段可以通过从最高相似性回溯过程之外的最高分位置开始回溯，即完成首次回溯之后，从首次回溯区域之外的最高分元素开始回溯，以得到第二个局部相似片段。

与尼德曼-翁施算法的比较

全局和局部比对

史密斯-沃特曼算法为局部比对算法，用于找出两序列中最相似的区域。尼德曼-翁施算法为全局比对算法，用于完整匹配两个序列。这两种算法的目不同，因此研究者在选择算法时要根据实际需求来决定。

两种算法都使用了置换矩阵，空位罚分，得分矩阵，以及回溯的方法，具有一定的相似度。然而，史密斯-沃特曼算法与尼德曼-翁施算法的三个主要区别在于：

	史密斯-沃特曼算法	尼德曼-翁施算法
初始化阶段	第一行和第一列全填充为 0	首行和首列需要考虑空位罚分
打分阶段	若得分为负，则分数为零	得分可以为负
回溯阶段	从最高分开始，回溯直至得分为 0	从右下角开始，回溯至左上角

其中，打分阶段分数不为负是非常重要的一点区别。它使得对序列局部的比对成为可能。当任何位置分数低于0，即表示此前的序列不具有相似性；而此时将此元素分数设为0，即达到了“重设”的效果，使得从此位置开始的比对不受之前位置的影响。初始化阶段的区别使得史密斯-沃特曼算法中从一序列任意位置开始匹配另一序列不受罚分，而尼德曼-翁施算法因为要匹配完整的序列，所以两端的空位也需要罚分。

置换矩阵

每一碱基对或残基对匹配或错配的分数通常用一矩阵表示，称为置换矩阵。基本的置换矩阵为匹配则加分，错配则扣分。以核苷酸序列为例，若匹配为+1，错配为-1，则置换矩阵为：

	A	G	C	T
A	1	-1	-1	-1
G	-1	1	-1	-1
C	-1	-1	1	-1
T	-1	-1	-1	1

该置换矩阵可以表示为： ${\displaystyle s(a_{i},b_{j})={\begin{cases}1,\quad a_{i}=b_{j}\\-1,\quad a_{i}\neq b_{j}\end{cases}}}$

不同的碱基对或残基对可以有不同的分数以适应于特定的场合。

氨基酸序列比对的置换矩阵一般更加复杂。通常性质相似的残基对具有正分数，反之，不相似的具有负分数。此外，残基对的相似或不相似程度决定了分数的大小。参见PAM（英语：Point accepted mutation），BLOSUM（英语：BLOSUM）。

空位罚分

当碱基对或残基对之间匹配会导致更低分数时，需要空位的引入，即让碱基或残基与空位匹配。空位罚分决定了插入或者删除的分值。最基本的空位罚分方式为每次插入或者删除的得分相同。然而在生物学上，两序列之间一般存在着具有不同相似度的区域。另外，单个基因突变事件可能导致一长串空位的插入。因此，一个连续的较长的空位优于多个分散的小的空位。虽然多个分散的小的空位可以产生更多匹配，但一个连续的较长的空位代表这个区域只在一个序列中出现，使用后者可以避免为了得到高分而过度匹配这段序列。实现该方法只需要引入空位起始罚分和空位延长罚分的概念。空位起始罚分通常高于空位延长罚分。例如EMBOSS Water （页面存档备份，存于互联网档案馆）的默认参数为空位起始罚分=10，空位延长罚分=0.5。

实际应用中空位罚分方法有多种（参见空位罚分（英语：Gap_penalty）），此处详细介绍这两种最常见的方法。设${\displaystyle W_{k}}$为空位罚分函数，其中${\displaystyle k}$为空位长度：

空位权值恒定模型

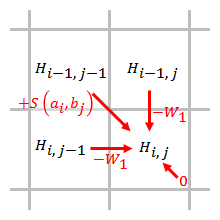
空位权值恒定情况下史密斯-沃特曼算法打分方法示意图

${\displaystyle W_{k}=kW_{1}}$

该模型空位的罚分正比于空位的长度。${\displaystyle W_{1}}$为单个空位的罚分。使用该模型时，原史密斯-沃特曼算法可简化为：

${\displaystyle H_{ij}=\max {\begin{cases}H_{i-1,j-1}+s(a_{i},b_{j}),\\H_{i-1,j}-W_{1},\\H_{i,j-1}-W_{1},\\0\end{cases}}}$

此时该算法步数为${\displaystyle O(mn)}$，${\displaystyle m}$和${\displaystyle n}$分别为两序列的长度。在对某一位置考虑空位罚分时，只需考虑相邻的上方的和左侧的位置，而不需考虑整列和整行。

空位延伸罚分模型

${\displaystyle W_{k}=u(k-1)+v\quad (u>0,v>0)}$

该模型考虑空位起始罚分和空位延长罚分，其中${\displaystyle v}$为开始空位的罚分，${\displaystyle u}$为每次延长空位的罚分。例如，一个长度为2的空位的罚分为${\displaystyle u+v}$。未经优化的该模型的算法步数为${\displaystyle O(m^{2}n)}$。Gotoh将该算法的步数优化至${\displaystyle O(mn)}$[2]，然而，优化后的方法只能找出一个局部比对结果，并且并不保证能成功获得结果[3]。Altschul进一步优化了Gotoh的算法，在保持复杂度不变的情况下解决了Gotoh算法的不足[3]。Myers和Miller指出，Gotoh和Altschul的算法忽视了Hirschberg在1975年提出的在线性空间内进行序列比对的方法[11]，并在改进的算法中运用了该方法[4]。Myers和Miller的算法仅使用${\displaystyle O(n)}$空间，${\displaystyle n}$为较短的序列的长度。

空位罚分例子

以两序列TACGGGCCCGCTAC和TAGCCCTATCGGTCA进行比对为例，分别考虑两种模型。

当使用空位权值恒定模型时，即不考虑空位起始和延长的区别，得到如下结果（置换矩阵为DNAfull，空位起始和延长均为1.0，其他参数为默认）：

TACGGGCCCGCTA-C
||   | || ||| |
TA---G-CC-CTATC
总得分为39.0

当使用空位延伸罚分模型时，设空位起始罚分为5.0，空位延长罚分为1.0时，得到如下结果：

TACGGGCCCGCTA
||   |||  |||
TA---GCC--CTA
总得分为27.0

可以看出，空位延伸罚分模型虽然总分略低，但考虑空位起始罚分和空位延长罚分能够有效避免多个小的空位。

得分矩阵

得分矩阵的作用是对两序列中两两位置进行打分以逐步记录最优比对。动态编程的思想体现于此。最终的最优局部比对结果是由逐步扩展当前位置最优比对结果来实现的（即通过作出一系列的对如何比对当前位置可以得到更高分数的决定来得到最终结果）。矩阵的长度和宽度分别为两序列长度+1。额外的首行和首列是为了让序列的末端可以和空位匹配。首行和首列均设为0。以CTCAA和GGTCA为例，初始得分矩阵为：

-	-	C	T	C	A	A
-	0	0	0	0	0	0
G	0
G	0
T	0
C	0
A	0

例子

以序列TGTTACGG和GGTTGACTA为例。使用如下参数：

• 置换矩阵：${\displaystyle s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}}$
• 空位罚分：${\displaystyle W_{k}=kW_{1},W_{1}=2}$

初始化得分矩阵，并进行打分。如下图所示。该图展示了该得分矩阵前三个元素的打分过程。黄色代表当前正在考虑的两个碱基。红色代表该位置得分的来源。

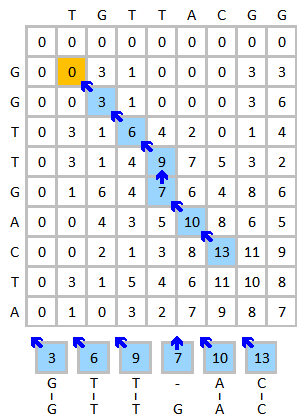
初始化得分矩阵（左1）以及部分打分过程（左2-左4）

打分完成后的得分矩阵如左下图所示。其中蓝色代表最高分元素。注意某些元素有不止一种得分来源，这样在回溯过程中会产生多个路径。如果有多个相同的最高分，则应当考虑每个最高分的回溯。回溯过程见右下图。局部最相似序列在从最高分回溯的过程中自右向左产生。

完成后的得分矩阵及最高分（蓝色）	回溯过程以及比对结果

该例的结果为：

G T T - A C
| | |   | |
G T T G A C

相关链接

• 生物信息学
• 序列比对
• 尼德曼-翁施算法
• 莱文斯坦距离
• BLAST

参考资料

1. Smith, Temple F.; and Waterman, Michael S. Identification of Common Molecular Subsequences (PDF). Journal of Molecular Biology. 1981, 147: 195–197 [2016-04-26]. PMID 7265238. doi:10.1016/0022-2836(81)90087-5. （原始内容存档 (PDF)于2016-01-21）. 
2. O. Gotoh. An Improved Algorithm For Matching Biological Sequences. Journal of Molecular Biology. 1982, 162: 705–708. doi:10.1016/0022-2836(82)90398-9. 
3. Stephen F. Altschul; and Bruce W. Erickson. Optimal Sequence Alignment Using Affine Gap Costs. Bulletin of Mathematical Biology. 1986, 48: 603–616. doi:10.1007/BF02462326. 
4. Eugene W. Myers; and Webb Miller. Optimal alignments in linear space. Computer applications in the biosciences. 1988, 4: 11–17. doi:10.1093/bioinformatics/4.1.11. 
5. Saul B. Needleman; and Christian D. Wunsch. A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology. 1970, 48: 443–453. doi:10.1016/0022-2836(70)90057-4. 
6. Sankoff D. Matching Sequences under Deletion/Insertion Constraints. Proceedings of the National Academy of Sciences of the United States of America. 1972, 69: 4–6. doi:10.1073/pnas.69.1.4. 
7. Thomas A. Reichert; Donald N. Cohen; and Andrew K.C. Wong. An application of information theory to genetic mutations and the matching of polypeptide sequences. Journal of Theoretical Biology. 1973, 42: 245–261. doi:10.1016/0022-5193(73)90088-X. 
8. William A. Beyer; Myron L. Stein; Temple F. Smith; and Stanislaw M. Ulam. A molecular sequence metric and evolutionary trees. Mathematical Biosciences. 1974, 19: 9–25. doi:10.1016/0025-5564(74)90028-5. 
9. Peter H. Sellers. On the Theory and Computation of Evolutionary Distances. Journal of Applied Mathematics. 1974, 26: 787–793. doi:10.1137/0126070. 
10. M.S Waterman; T.F Smith; and W.A Beyer. Some biological sequence metrics. Advances in Mathematics. 1976, 20: 367–387. doi:10.1016/0001-8708(76)90202-4. 
11. D. S. Hirschberg. A linear space algorithm for computing maximal common subsequences. Communications of the ACM. 1975, 18: 341–343. doi:10.1145/360825.360861. 

外部链接

• （英文）JAligner（页面存档备份，存于互联网档案馆） — 一个Java实现的史密斯-沃特曼算法的开源程序
• （英文）B.A.B.A.（页面存档备份，存于互联网档案馆） — 一个带源代码并且动态解释该算法的应用
• （英文）FASTA/SSEARCH （页面存档备份，存于互联网档案馆） — 欧洲生物信息研究所提供的在线服务
• （英文）diagonalsw （页面存档备份，存于互联网档案馆） — 一个C/C++实现的史密斯-沃特曼算法的程序，具有并行处理能力
• （英文）SSW （页面存档备份，存于互联网档案馆） — 一个C/C++实现的史密斯-沃特曼算法的程序，具有并行处理能力